Кривые Гильберта и Серпинского, или снова рекурсия

Д.М.Златопольский

Окончание. Начало см. в № 8/99

В предыдущем номере мы рассмотрели алгоритм построения кривой Гильберта. Напомним, что речь идет о так называемых “всюду плотных в квадрате кривых”. Это означает, что для любой точки квадрата найдется кривая некоторого порядка, проходящая через эту точку. В продолжение темы рассмотрим еще одну кривую данного класса — кривую Серпинского. Эта кривая замечательна тем, что является замкнутой кривой без самопересечений, всюду плотной в квадрате.

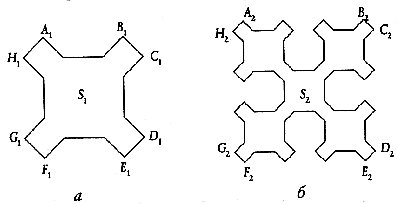
На рис. 1 представлены две кривые Серпинского: первого (рис. 1а) и второго (рис. 1б) порядков. Обратим внимание на важную особенность кривых Серпинского: длина горизонтальных и вертикальных отрезков кривых в два раза больше длины горизонтальных и вертикальных проекций наклонных отрезков.

Р РёСЃ. 1.
Кривые Серпинского первого и второго порядков

Как построить кривую Серпинского? Попытка по аналогии с алгоритмом построения кривой Гильберта использовать в качестве основного “строительного блока” кривую S1 на рис. 1а (возможно, без одного ребра) не приведет нас к нужному решению. Кривая Серпинского состоит из четырех звеньев, каждое из которых строится рекурсивно, соединенных четырьмя отрезками. На рис. 1 эти отрезки обозначены BC, DE, FG и HA. С учетом этого можно увидеть, что рекурсивно строятся звенья AB, CD, EF и GH.

Если процедуры рисования четырех звеньев кривой обозначить соответственно LineAB, LineCD, LineEF и LineGH, а отрезков BC, DE, FG и HA — соответственно SegmBC, SegmDE, SegmFG и SegmAH, то фрагмент, относящийся к построению кривой Серпинского (по часовой стрелке), в программе на школьном алгоритмическом языке имеет вид:
...
LineAB
SegmBC
LineCD
SegmDE
LineEF
SegmFG
LineGH
SegmHA
РєРѕРЅ

Напомним, что звенья AB, CD, EF и GH строятся рекурсивно. Чтобы получить схемы их построения, проанализируем структуру кривой A2B2 на рис. 1б. Можно увидеть, что она состоит из линий, подобных кривым A1B1, C1D1, G1H1 и A1B1 на рис. 1а, соединенных отрезками, аналогичными отрезкам B2C2 и H2A2, а также горизонтальным отрезком двойной длины (см. выше), т.е. рекурсивная схема построения кривой AB i-го порядка следующая:

AB(i):    AB(i–1);    BC;     CD(i–1);    В®;
                 GH(i–1);   HA;     AB(i–1)

Соответствующая рекурсивная процедура имеет вид:

алг LineAB(арг цел i)
  нач
  если i>0
   то
   LineAB(i-1)
   SegmBC
   LineCD(i-1)
   SegmEast
   LineGH(i-1)
   SegmHA
   LineAB(i-1)
  РІСЃРµ
РєРѕРЅ
— где SegmBC, SegmHA и SegmEast — процедуры рисования отрезков BC, HA и отрезка, изображенного на схеме в виде символа ®.

Аналогично можно получить схемы построения кривых CD, EF и GH:

CD(i): CD(i–1); DE; EF(i–1); Ї;
AB(i–1); BC; CD(i–1)
EF(i): EF(i–1); FG;   GH(i–1); В¬;
CD(i–1); DE; EF(i–1)
GH(i): GH(i–1); HA; AB(i–1); ;
EF(i–1); FG; GH(i–1)

  Рекурсивные процедуры РёС… построения:

алг LineCD(арг цел i)
нач
  если i>0
  то
   LineCD(i-1)
   SegmDE
   LineEF(i-1)
   SegmSouth
   LineAB(i-1)
   SegmBC
   LineCD(i-1)
   РІСЃРµ
РєРѕРЅ

алг LineEF(арг цел i)
нач
  если i>0
  то
    LineEF(i-1)
    SegmFG
    LineGH(i-1)
    SegmWest
    LineCD(i-1)
    SegmDE
    LineEF(i-1)
  РІСЃРµ
РєРѕРЅ

алг LineGH(арг цел i)
  нач
   если i>0
   то
     LineGH(i-1)
     SegmHA
     LineAB(i-1)
     SegmNord
     LineEF(i-1)
     SegmFG
     LineGH(i-1)
   РІСЃРµ
РєРѕРЅ

Длину горизонтальной (и вертикальной) проекции наклонных отрезков кривой обозначим h и учтем, что горизонтальные и вертикальные отрезки имеют длину 2h. Тогда процедуры рисования отрезков, показанных на схемах в виде символов ® Ї ¬ , можно записать как:

алг SegmEast
нач
  | вектор(2*h, 0)
РєРѕРЅ

алг SegmSouth
нач
  | вектор(0, 2*h) 
РєРѕРЅ

алг SegmNord
  нач
   | вектор(0, -2*h)
  РєРѕРЅ

алг SegmWest
  нач
   | вектор(-2*h, 0)
  РєРѕРЅ

Процедуры рисования наклонных отрезков SegmBC, SegmDE, SegmFG, SegmHA имеют вид:

алг SegmBC
нач
  | вектор(h, h)
РєРѕРЅ

алг SegmDE
нач
  | вектор(-h, h)
РєРѕРЅ

алг SegmFG
  нач
   | вектор(-h, -h)
  РєРѕРЅ

алг SegmHA
  нач
   | вектор(h, -h)
  РєРѕРЅ

Выразим теперь параметр h кривой Серпинского через длину стороны опорного квадрата, которую обозначим как A. Выше показано, что кривая Серпинского порядка i состоит из центрального квадрата со срезанными углами, а к каждому срезу примыкает кривая Серпинского порядка i –1, см. рис. 2. Проведем главную диагональ опорного квадрата, соединяющую левую верхнюю вершину Tlu с правой нижней Trd. Она пересечет кривую порядка i в точках Сlu и Сrd, а линии среза центрального квадрата – в точках Klu и Krd. Назовем отрезок, соединяющий точки Сlu и Сrd диагональю кривой Серпинского, его длину обозначим d i, кроме того, введем относительную длину диагонали кривой Серпинского Si=di/h. Расстояние между точками Klu и Krd обозначим через p. Выполнив несложные геометрические выкладки, найдем, что p=h. Поскольку отрезки [Сlu, Klu] и [Сrd, Krd] являются диагоналями кривых Серпинского порядка i –1, то di = 2 di–1 + p или в относительных величинах

Si =2Si–1+ (*)

причем из рассмотрения кривой первого порядка следует, что S0 =. Нам понадобится не относительная длина диагонали кривой Серпинского Si, а величина Zi = Si/ , которую назовем коэффициентом диагонали кривой Серпинского. Разделив уравнение (*) на , получим

Zi =2 Zi–1+3 (**)

причем Z0 = 1. Отсюда следует, что коэффициенты Zi – натуральные числа. Уравнение (**) позволяет найти (используя, в частности, рекурсию) Zi для любого i. Из того же рис. 2 видно, что диагональ опорного квадрата Dsq (как известно, Dsq = A ) выражается через диагональ кривой Серпинского соотношением: Dsq = dn + h. Выражая dn через Sn, а эту величину через Zn, получаем: Dsq = h (Zn +1)serp15.gif (94 bytes). С другой стороны, как известно, Dsq=A. Приравнивая эти два выражения для Dsq, находим величину h:

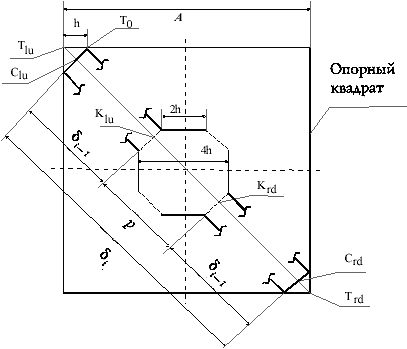
Р РёСЃ. 2

Теперь легко найти положение начальной точки кривой Серпинского T0: она находится правее точки Tlu на величину h. В свою очередь координаты этой точки находятся, если учесть, что опорный квадрат расположен по центру экрана:

Xtlu=Xc — A/2; Ytlu=Yc — A/2

Приведем рекурсивную фукцию calcZ, вычисляющую коэффициент длины диагонали кривой Серпинского порядка i:

алг цел calcZ(арг цел i)
  нач
   если i=0
    то знач:=1
    иначе знач:=2*calcS(i-1)+3
   РІСЃРµ
  РєРѕРЅ

Приведем программы построения кривой Серпинского данного порядка.
 
Школьный алгоритмический язык:

цел h |глобальные переменные
алг Кривая Серпинского
  нач цел n, x0, y0,Xlu,Ylu,Hscr,Wscr,A,Z
   вещ PrA
    Hscr:=480 |Высота экрана
    Wscr:=640 |РЁРёСЂРёРЅР° экрана
     |Р’РІРѕРґРёРј исходные данные для построения
     |РєСЂРёРІРѕР№ Серпинского
    РЅС†
     вывод РЅСЃ, "Введите длину стороны
               РѕРїРѕСЂРЅРѕРіРѕ квадрата"
     вывод , "РІ % РѕС‚ высоты экрана"
     РІРІРѕРґ PrA
   РєС† РїСЂРё PrA<100
   вывод РЅСЃ, "Введите РїРѕСЂСЏРґРѕРє РєСЂРёРІРѕР№"
   РІРІРѕРґ n
   A:=Int(PrA/100*Hscr)
    |Сторона РѕРїРѕСЂРЅРѕРіРѕ квадрата
   Z:=calcZ(n)
    |Коэффициент диагонали РєСЂРёРІРѕР№ Серпинского
   h:=Int(A/(Z+1))|Проекция наклонного отрезка
    |Находим координаты левой верхней
    |точки РѕРїРѕСЂРЅРѕРіРѕ квадрата
   Xlu:=Div(Wscr,2) - Div(A,2)
   Ylu:=Div(Hscr,2) - Div(A,2)
    |Находим координаты начальной точки РєСЂРёРІРѕР№
   y0:=Ylu
   x0:=Xlu+h
   видео(17) |VGA экран 640*480
   РїРѕР·(x0,y0)
   LineAB(n)
   SegmBC
   LineCD(n)
   SegmDE
   LineEF(n)
   SegmFG
   LineGH(n)
   SegmHA
   видео(0)
РєРѕРЅ

Как и при построении кривой Гильберта, в этой программе не хватает задержки, позволяющей проследить процесс построения кривой. В остальных программах она используется.
 
Язык Паскаль

Uses CRT,Graph;
const
del=5000;{Время задержки}
Var d,r: integer;
n: byte;
Xlu,Ylu,Hscr,Wscr,A,x0,y0,h,Z: word;
PrA:real;
function calcZ(i:byte):word;
   {Функция, рекурсивно вычисляющая коэффициент
    диагонали РєСЂРёРІРѕР№ Серпинского}
begin
   if i=0 then calcZ:=1
     else calcZ:=2*calcZ(i–1)+3;
end;
  {Процедуры рисования наклонных, горизонтальных Рё вертикальных отрезков РєСЂРёРІРѕР№}
Procedure SegmBC; begin Linerel(h, h) end;
Procedure SegmDE; begin Linerel(-h, h) end;
Procedure SegmFG; begin Linerel(-h, -h) end;
Procedure SegmHA; begin Linerel(h, -h) end;
Procedure SegmEast; begin Linerel(2*h, 0) end;
Procedure SegmSouth; begin Linerel(0, 2*h) end;
Procedure SegmWest; begin Linerel(-2*h, 0) end;
Procedure SegmNord; begin Linerel(0, -2*h) end;
  {Pекурсивные процедуры рисования четырех
   частей РєСЂРёРІРѕР№ Серпинского}
Procedure LineCD(i: byte); forward;
Procedure LineGH(i: byte); forward;
Procedure LineEF(i: byte); forward;
Procedure LineAB(i: byte);
begin
    if i>0 then begin
      LineAB(i-1); SegmBC; LineCD(i-1); SegmEast;
      LineGH(i-1); SegmHA; LineAB(i-1); delay(del);
    end
end;
Procedure LineCD;
  begin
   if i>0 then begin
    LineCD(i-1); SegmDE; LineEF(i-1); SegmSouth;
    LineAB(i-1); SegmBC; LineCD(i-1); delay(del);
   end
  end;
Procedure LineEF;
  begin
   if i>0 then begin
    LineEF(i-1); SegmFG; LineGH(i-1); SegmWest;
    LineCD(i-1); SegmDE; LineEF(i-1); delay(del);
  end
end;
Procedure LineGH;
  begin
   if i>0 then begin
    LineGH(i-1); SegmHA; LineAB(i-1); SegmNord;
    LineEF(i-1); SegmFG; LineGH(i-1); delay(del);
   end
end;
BEGIN {Основной программы}
  clrscr; {Чистка экрана}
  write('Введите длину стороны РѕРїРѕСЂРЅРѕРіРѕ
     квадрата');
  write('РІ % РѕС‚ высоты экрана ');
  readln(PrA);
  write('Введите РїРѕСЂСЏРґРѕРє РєСЂРёРІРѕР№ ');
  readln(n);
  d:=detect;
  initgraph(d, r, '');
   {Переход РІ графический режим}
  Hscr:=GetMaxY+1;
  Wscr:=GetMaxX+1;{Высота Рё ширина экрана}
  Z:=calcZ(n);
   {Коэффициент диагонали РєСЂРёРІРѕР№ Серпинского}
  h:=round(A/(S+1));
   {Проекция наклонного отрезка}
   {Находим координаты левой верхней
    точки РѕРїРѕСЂРЅРѕРіРѕ квадрата}
  Xlu:=Wscr div 2 - a div 2;
  Ylu:=Hscr div 2 - a div 2;
   {Находим координаты начальной точки РєСЂРёРІРѕР№}
  y0:=Ylu; x0:=Xlu+h;
  moveto(x0, y0);
   {Ставим графический РєСѓСЂСЃРѕСЂ РІ начальную точку}
   {Строим РєСЂРёРІСѓСЋ}
  LineAB(n); SegmBC; LineCD(n); SegmDE;
  LineEF(n); SegmFG; LineGH(n); SegmHA;
  readln;{Выход - нажатием клавиши Enter}
  closegraph;{Переход РІ текстовый режим}
END.

Язык Бейсик
    'Функция, рекурсивно вычисляющая коэффициент
    'диагонали РєСЂРёРІРѕР№ Серпинского
  DECLARE FUNCTION calcZ% (i AS INTEGER)
  DECLARE SUB delay (del&) 'Задеpжка
    'Процедуры рисования наклонных, горизонтальных
    'Рё вертикальных отрезков РєСЂРёРІРѕР№
  DECLARE SUB SegmBC () : DECLARE SUB SegmDE ()
  DECLARE SUB SegmFG () : DECLARE SUB SegmHA ()
  DECLARE SUB SegmEast () : DECLARE SUB SegmSouth ()
  DECLARE SUB SegmWest () : DECLARE SUB SegmNord ()
    'Pекурсивные процедуры рисования четырех
    'частей РєСЂРёРІРѕР№ Серпинского
  DECLARE SUB LineAB (i AS INTEGER)
  DECLARE SUB LineCD (i AS INTEGER)
  DECLARE SUB LineEF (i AS INTEGER)
  DECLARE SUB LineGH (i AS INTEGER)
  DIM SHARED del&: del& = 200000
    'РїР°pаметp задеpжки
  Hscr! = 480: Wscr! = 640
    'Высота Рё шиpРёРЅР° СЌРєpана
  DIM SHARED h AS SINGLE
  DIM Xlu AS SINGLE, Ylu AS SINGLE, x0 AS SINGLE, y0 AS SINGLE
  DIM A AS SINGLE, PrA AS SINGLE
  DIM n AS INTEGER, Z AS INTEGER
  CLS 'Чистка экрана
    'Р’РІРѕРґРёРј исходные данные для построения
    'РєСЂРёРІРѕР№ РЎРµpРїРёРЅСЃРєРѕРіРѕ
  DO
    PRINT "Введите длину стороны РѕРїРѕСЂРЅРѕРіРѕ квадрата";
    INPUT " РІ % РѕС‚ высоты экрана", PrA
  LOOP UNTIL PrA < 100
  INPUT "Введите РїРѕСЂСЏРґРѕРє РєСЂРёРІРѕР№ ", n
  A = PrA / 100! * Hscr!
     'Сторона РѕРїРѕСЂРЅРѕРіРѕ квадрата
  Z = calcZ%(n)
  'Коэффициент диагонали РєСЂРёРІРѕР№ Серпинского
  h = A / (Z + 1)
     'Проекция наклонного отрезка
     'Находим координаты левой верхней точки
     'РѕРїРѕСЂРЅРѕРіРѕ квадрата
  Xlu = Wscr! / 2 - A / 2
  Ylu = Hscr! / 2 - A / 2
    ' Находим координаты начальной точки РєСЂРёРІРѕР№
  y0 = Ylu: x0 = Xlu + h
    'РџРµpеход РІ Ріpафический pежим для монитора
    'VGA. Р­Рєpан 640*480
  SCREEN (12)
    'Графический РєСѓСЂСЃРѕСЂ устанавливаем РІ
    'начальную точку
  PSET (x0, y0)
    'Строим РєСЂРёРІСѓСЋ
  CALL LineAB(n): CALL SegmBC
  CALL LineCD(n): CALL SegmDE
  CALL LineEF(n): CALL SegmFG
  CALL LineGH(n): CALL SegmHA
  DO: LOOP UNTIL INKEY$ = CHR$(13)
    'Выход - нажатием клавиши Enter
  SCREEN 0 'Переходим РІ текстовый режим
END
FUNCTION calcZ% (i AS INTEGER)
    'Функция, рекурсивно вычисляющая коэффициент
    'диагонали РєСЂРёРІРѕР№ Серпинского
  IF i = 0 THEN
    calcZ% = 1
  ELSE
    calcZ% = 2 * calcZ%(i - 1) + 3
  END IF
END FUNCTION
SUB delay (del&)
    'Задеpжка СЃ помощью пустого цикла
  DIM i&: FOR i& = 1 TO del&: NEXT i&
END SUB
SUB LineAB (i AS INTEGER)
  IF i > 0 THEN
    CALL LineAB(i - 1): CALL SegmBC
    CALL LineCD(i - 1): CALL SegmEast
    CALL LineGH(i - 1): CALL SegmHA
    CALL LineAB(i - 1): CALL delay(del&)
  END IF
END SUB
SUB LineCD (i AS INTEGER)
   IF i > 0 THEN
     CALL LineCD(i - 1): CALL SegmDE
     CALL LineEF(i - 1): CALL SegmSouth
     CALL LineAB(i - 1): CALL SegmBC
     CALL LineCD(i - 1): CALL delay(del&)
  END IF
END SUB
SUB LineEF (i AS INTEGER)
   IF i > 0 THEN
     CALL LineEF(i - 1): CALL SegmFG
     CALL LineGH(i - 1): CALL SegmWest
     CALL LineCD(i - 1): CALL SegmDE
     CALL LineEF(i - 1): CALL delay(del&)
  END IF
END SUB
SUB LineGH (i AS INTEGER)
    IF i > 0 THEN
       CALL LineGH(i - 1): CALL SegmHA
       CALL LineAB(i - 1): CALL SegmNord
       CALL LineEF(i - 1): CALL SegmFG
       CALL LineGH(i - 1): CALL delay(del&)
   END IF
END SUB
SUB SegmBC
    LINE -STEP(h, h)
END SUB
SUB SegmDE
    LINE -STEP(-h, h)
END SUB
SUB SegmEast
    LINE -STEP(2 * h, 0)
END SUB
SUB SegmFG
    LINE -STEP(-h, -h)
END SUB
SUB SegmHA
    LINE -STEP(h, -h)
END SUB
SUB SegmNord
    LINE -STEP(0, -2 * h)
END SUB
SUB SegmSouth
    LINE -STEP(0, 2 * h)
END SUB
SUB SegmWest
    LINE -STEP(-2 * h, 0)
END SUB

Язык Си
#include<stdio.h>
#include <graphics.h>
#include <math.h>
#include <conio.h>
#include <dos.h>
#include<stdlib.h>
#define PATH "" /* файлы *.BGI находятся в pабочем каталоге */
#define del 5000 /* Время задержки */
int h;
    /* Округление вещественного числа РґРѕ ближайшего целого */
int round(float a) {return (int)floor(a+0.5);}
    /* Функция, рекурсивно вычисляющая коэффициент диагонали РєСЂРёРІРѕР№ Серпинского */
int calcZ(int i)
   {if (i==0) return 1;
      else return 2*calcZ(i-1)+3;
   }
    /*Функции рисования наклонных, горизонтальных Рё вертикальных отрезков РєСЂРёРІРѕР№ */
void SegmBC() {linerel(h,h);}
void SegmDE() {linerel(-h,h);}
void SegmFG() {linerel(-h,-h);}
void SegmHA() {linerel(h,-h);}
void SegmEast() {linerel(2*h,0);}
void SegmSouth() {linerel(0, 2*h);}
void SegmWest() {linerel(-2*h,0);}
void SegmNord() {linerel(0,-2*h);}
    /*Pекурсивные функции рисования четырех частей РєСЂРёРІРѕР№ Серпинского */
void LineCD(int);
void LineGH(int);
void LineEF(int);
void LineAB(int i)
   {if (i>0)
      {LineAB(i-1); SegmBC(); LineCD(i-1);
        SegmEast();
        LineGH(i-1); SegmHA(); LineAB(i-1);
        delay(del);
      }
  }
void LineCD(int i)
{if (i>0)
      {LineCD(i-1); SegmDE(); LineEF(i-1);
         SegmSouth();
         LineAB(i-1); SegmBC(); LineCD(i-1);
        delay(del);
      }
  }
void LineEF(int i)
   {if (i>0)
      {LineEF(i-1); SegmFG(); LineGH(i-1);
       SegmWest();
       LineCD(i-1); SegmDE(); LineEF(i-1);
      delay(del);
      }
  }
void LineGH(int i)
  {if (i>0)
      {LineGH(i-1); SegmHA(); LineAB(i-1);
        SegmNord();
        LineEF(i-1); SegmFG(); LineGH(i-1);
        delay(del);
       }
  }
void main()
{int d=DETECT,r,n,A,Xlu,Ylu,x0,y0,Hscr,Wscr,Z;
   float PrA;
    clrscr();/*Очистка экрана*/
         /*Р’РІРѕРґРёРј исходные данные для построения РєСЂРёРІРѕР№ Серпинского*/
  do
    {printf("\nВведите длину стороны   РѕРїРѕСЂРЅРѕРіРѕ квадрата");
      printf("РІ % РѕС‚ высоты экрана ");
      scanf("%f",&PrA);
    }
  while (PrA>=100);
printf("\nВведите порядок кривой");
scanf("%d",&n);
initgraph(&d, &r, "");
     /* РџРµpеход РІ Ріpафический pежим */
Hscr=getmaxy()+1; 
Wscr=getmaxx()+1;
    /*Высота Рё ширина экрана*/
A=round(PrA/100*Hscr);
    /*Сторона квадрата*/
Z=calcZ(n);
     /*Коэффициент диагонали РєСЂРёРІРѕР№ Серпинского*/
h=round(A/(Z+1));
   /*Проекция наклонного отрезка*/
   /*Находим координаты левой верхней точки РѕРїРѕСЂРЅРѕРіРѕ квадрата*/
Xlu=Wscr/2 - A/2; 
Ylu=Hscr/2 - A/2;
     /*Находим координаты начальной точки РєСЂРёРІРѕР№*/
y0=Ylu; x0=Xlu+h;
moveto(x0, y0);
    /*Ставим графический РєСѓСЂСЃРѕСЂ РІ начальную точку*/
   /*Строим РєСЂРёРІСѓСЋ*/
LineAB(n); SegmBC(); LineCD(n);
SegmDE();
LineEF(n); SegmFG(); LineGH(n);
SegmHA();
getch();
    /*Выход - нажатием любой клавиши*/
closegraph();
   /*Переход РІ текстовый режим*/ }

TopList