СЕМИНАР
Системы счисления и их применения*
С.Б. Гашков,
Москва
Окончание. Начало в № 2, 3,
4/2006.
§ 15. Признаки делимости
Рассказывая о системах счисления,
нельзя обойти вниманием признаки делимости.
Напомним широко известные признаки делимости в
случае использования десятичной системы
счисления. Простейший из них следующий: остаток
от деления некоторого числа на 2n равен
остатку от деления на 2n числа,
записанного последними его n цифрами.
Аналогичный признак справедлив для 5n и
любого числа вида 2л5ь, где max(m,
k) = n. Чуть более сложен в применении
признак делимости на 9: сумма цифр данного числа
имеет тот же остаток от деления на 9, что и само
число. Такой же признак справедлив и для
делимости на 3.
Подобный же признак можно предложить и
для делимости на число 9...9, состоящее из n
девяток: надо разбить испытуемое число на n-разрядные
блоки, начиная с младших разрядов, и всех их
сложить (блок, образованный старшими разрядами,
может быть короче); у полученного числа будет тот
же остаток от деления, что и у исходного. Так как 99
делится на 11, то таким способом можно найти и
остаток от деления на 11. Учитывая, что 999 делится
на 111 и, следовательно, на 37, получаем признаки
делимости на эти числа.
Но есть более эффективный признак
делимости
на 11: надо складывать цифры числа, начиная с
младших, чередуя знаки (первая цифра берется со
знаком плюс) — полученное число имеет тот же
остаток от деления на 11, что и исходное.
Аналогичный признак делимости имеется
и для числа 10...01, запись которого, кроме двух
единиц, содержит n нулей. Испытуемое число
разбивается на (n + 1)-разрядные блоки, начиная
с младших разрядов (блок, образованный старшими
разрядами, может быть короче), и все они
складываются с чередующимися знаками (первое
число берется со знаком плюс). Полученный
результат имеет тот же остаток от деления, что и
испытуемое число. Поскольку 1001 = 11 · 7 · 13, мы
попутно получаем таким путем признаки делимости
на 7, 13, 91, 77, 143.
 23.
Докажите сформулированные признаки делимости. 23.
Докажите сформулированные признаки делимости.
При применении рассмотренных
признаков к большим числам получаются меньшие,
но все же достаточно большие числа, имеющие те же
остатки от деления, что и исходные. К ним нужно
применить еще раз тот же признак делимости и т.д.
Часто эффективность этих признаков при
применении к большим числам все же ненамного
выше простого деления.
Есть, однако, случаи, когда только
применение признаков делимости позволяет найти
остаток, так как непосредственное деление
практически невозможно ввиду колоссальной
вычислительной сложности.
 24.
Найдите остаток от деления 4444444444 на 99. 24.
Найдите остаток от деления 4444444444 на 99.
Число 4444444444 состоит более чем из
200 000 цифр, и его прямое вычисление требует
порядка миллиарда операций. Правда, кроме
признаков делимости на 9 и 11, здесь надо применить
и некоторые соображения, связанные с делимостью
степеней. Другой способ решения этой задачи —
применение калькулятора и бинарного метода
возведения в степень.
Полезны признаки делимости и при
разгадывании ребусов, подобных следующему.
 25.
Замените звездочки на пропущенные цифры в
примере 25.
Замените звездочки на пропущенные цифры в
примере 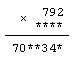
Признаки делимости могут помочь в
нахождении ошибки при выполнении умножения
больших чисел. Простейший из способов контроля —
проверка по модулю 9. Этому способу обучали еще в
средневековых университетах: у обоих множителей
находятся остатки от деления на 9, потом исходные
числа перемножаются и у результата опять
находится остаток от деления на 9, который
сравнивается с остатком от деления на 9
произведения исходных чисел, подлежащего
проверке. Если остатки разные, то произошла
ошибка. Если известно, что ошибка только в одном
разряде, то можно точно указать величину ошибки,
но не ее положение. В случае совпадения
результатов остается возможность одной ошибки
типа замены 0 на 9 или наоборот, а также нескольких
ошибок. В этом случае можно провести еще
аналогичную проверку по модулю 11, которая или
подтвердит существование ошибки указанного
вида, или установит наличие нескольких ошибок
(или их отсутствие).
§ 16. Арифметические коды
Можно установить точно положение
ошибки и даже исправить ее, в предположении, что
она только одна. Для этого надо применить так
называемые “арифметические коды”. Приведем их
простейший пример.
Допустим, что при перемножении
десятичных чисел получилось 15-разрядное число с
ошибкой в одном разряде. Для нахождения величины
ошибки применим проверку по модулю 9 и найдем, что
она по модулю 9 равна a. Если ошибка произошла
в i-м разряде12, то величина ошибки в
произведении равна a · 10i–1 или (a –
9) · 10i–1, а если a = 0, то или ошибки не
было, или она равна ± 9 · 10i–1. Применим
проверку по модулю 31. После нее станет известно
значение ошибки b по модулю 31. Если остаток по
модулю 31 равен нулю, то ошибки не было.
Пусть он не равен нулю. Выпишем остатки
от деления чисел 10, ..., 1015 на 31. Они равны
10, 7, 8, 18, 25, 2, 20, 14, 16, 5, 19, 4, 9, 28, 1. Заметим, что
невозможно равенство по модулю 31 чисел a · 10i
и (a – 9) · 10о, так как тогда при
некоторых a = 1, 2, 3, 4 и i = 0, 1, ..., 14 были бы
равны по модулю 31 числа a ·10i и a
– 9, а невозможность этого проверяется
непосредственно с помощью вычисленной выше
последовательности остатков. Точно так же
проверяется невозможность совпадения по модулю
31 чисел 9 · 10i и (–9) · 10j.
Вычисляя остатки по модулю 31 у всех чисел a · 10i
и (a – 9) · 10i при i = 1, ..., 15 и
сравнивая их с найденным ранее остатком, находим
значение i и точную величину ошибки a или a
– 9. Аналогично поступаем в случае ошибки ±9 · 10i.
Приведенный пример арифметического
кода иллюстрирует принципиальную возможность их
построения, на первый взгляд кажущуюся
парадоксальной. Прикладного значения при ручных
вычислениях он не имеет хотя бы потому, что, как
можно проверить, проще еще раз перемножить эти
числа, чем выполнять указанные выше операции.
Но такие алгоритмы применяют для
контроля правильности работы арифметических
устройств, и этот контроль осуществляет
специальный блок в таком устройстве. В
рассматриваемом случае сложность устройства со
встроенным арифметическим кодом рассмотренного
вида увеличивается не более чем в два раза. Если
рассмотреть подобные коды с достаточно большой
длиной (p – 1)/2 и проверочными множителями 9 и p,
где p — простое число вида 280k + 31 такое, что
10(p–1)/2 при делении на p дает остаток
1, а 10k при k < (p – 1)/2 при делении
на p дают остатки, отличные от 1 (в
рассмотренном случае p равнялось 31, а k —
нулю), то сложность исправления ошибки будет мала
при больших p в сравнении со сложностью
умножения (p – 1)/2-разрядных чисел.
На самом деле на практике для
повышения надежности арифметических устройств
используются не десятичные, как рассмотренный, а
двоичные коды, но они устроены подобным же
образом.
 26. Примените
указанный арифметический код для расшифровки
ребуса 26. Примените
указанный арифметический код для расшифровки
ребуса
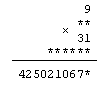
Можно с помощью этого кода
расшифровать и ребус, в котором ровно в одном
разряде результата имеется ошибка, но неизвестно
в каком. Тот же код можно использовать для
демонстрации арифметического фокуса: вы
предлагаете вашему другу задумать два не слишком
больших числа, перемножить их, и результат
умножить на якобы случайное число 279, а потом
сообщить вам ответ с одной ошибкой в каком-нибудь
разряде. Используя указанный код (если перед этим
предварительно подготовить все нужные таблицы и
немного потренироваться), вы быстро укажете эту
ошибку. Заметьте, что полный перебор вариантов
требует в случае 15-разрядного ответа 134-кратного
деления предполагаемого ответа на 279.
§ 17. Минимальные формы двоичной записи с
цифрами 0 и ±1 и первая попытка уменьшить
сложность умножения
В позиционных системах счисления с
заданным основанием b можно, кроме обычных
цифр, использовать и отрицательные цифры –1, –2,
..., –(b–1). Правда, это приводит к
неоднозначности в записи чисел. Зато таким
образом можно уменьшить количество ненулевых
цифр в записи и их величину. Далее в этом
параграфе мы будем рассматривать случай b = 2,
т. е. записи чисел в двоичной системе с цифрами –1,
0, 1.
 27.
Приведите пример числа, для которого существуют
по крайней мере две 27.
Приведите пример числа, для которого существуют
по крайней мере две
записи описанного вида с
минимальным возможным числом ненулевых цифр.
Назовем двоичную запись с
использованием отрицательных единиц минимальной
формой, если в ней нет соседних ненулевых цифр.
Для этого определения не очевидна ни
единственность минимальной формы, ни
минимальность длины минимальной формы. Однако и
то и другое верно, т.е. минимальная форма
определена однозначно и содержит наименьшее
количество ненулевых цифр среди всех возможных
форм двоичной записи числа с использованием
отрицательных единиц.
Докажем это. Пусть 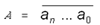 — произвольная двоичная запись
числа a, т.е. a = 2nan + ... + 2a1
+ a0, где ai = 0, ±1. Далее вместо –1
будем писать — произвольная двоичная запись
числа a, т.е. a = 2nan + ... + 2a1
+ a0, где ai = 0, ±1. Далее вместо –1
будем писать 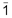 .
Обозначим через v(A) количество ненулевых
цифр в этой записи и через .
Обозначим через v(A) количество ненулевых
цифр в этой записи и через 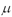 (A) — количество пар соседних
ненулевых цифр. Заметим, что 2k + 2k+1
+ ... + 2m-1 = 2m – 2k,
поэтому, выполняя в записи A следующие
преобразования: (A) — количество пар соседних
ненулевых цифр. Заметим, что 2k + 2k+1
+ ... + 2m-1 = 2m – 2k,
поэтому, выполняя в записи A следующие
преобразования:
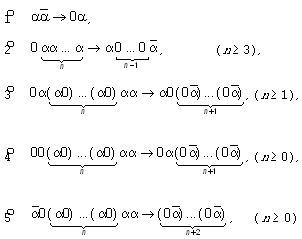
(где для 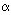 = 1, = 1, 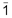 ,
соответственно, ,
соответственно, 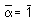 ,
1), мы не меняем записываемого числа, не
увеличиваем величин v(A) и ,
1), мы не меняем записываемого числа, не
увеличиваем величин v(A) и 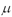 (A) и всегда уменьшаем их
сумму: (A) и всегда уменьшаем их
сумму:

Будем выполнять эти преобразования,
пока это возможно. Так как величина v(A) + 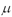 (A) не может
неограниченно уменьшаться, то в конце концов
получим запись числа a, в которой нельзя будет
выполнить ни одну из этих операций. (A) не может
неограниченно уменьшаться, то в конце концов
получим запись числа a, в которой нельзя будет
выполнить ни одну из этих операций.
 28.
Докажите, что если в записи невозможно выполнить
ни одну из указанных операций, то в этой записи
нигде не будет встречаться соседних ненулевых
цифр. 28.
Докажите, что если в записи невозможно выполнить
ни одну из указанных операций, то в этой записи
нигде не будет встречаться соседних ненулевых
цифр.
Докажем единственность минимальной
формы для данного числа a. Допустим, что есть
две разные минимальные формы A и B. Тогда
они заканчиваются одинаковым числом нулей в
младших разрядах, иначе, если бы одна
заканчивалась k нулями, а другая m > k
нулями, то наше число делилось бы на 2m, а
с другой стороны, делилось бы только на 2k,
но не на 2k+1, что невозможно. Аналогично
получаем, что их последние ненулевые цифры равны,
так как в противном случае наше число имело бы
при делении на 2m+2 (где m — число
нулей в конце) в остатке разные числа 2m
и 2m+2 – 2m (так как в конце одной
записи стоят цифры 010 ... 0, а в конце другой — цифры
0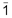 ... 0 ввиду
отсутствия пар ненулевых цифр в обеих записях).
Отбрасывая равные последние цифры от обеих
записей, получаем более короткие различные
записи для равных чисел. Повторяя для этих
записей проведенное рассуждение, получим,
наконец, что число ±1 или 0 имеет две разные
записи, а это невозможно. ... 0 ввиду
отсутствия пар ненулевых цифр в обеих записях).
Отбрасывая равные последние цифры от обеих
записей, получаем более короткие различные
записи для равных чисел. Повторяя для этих
записей проведенное рассуждение, получим,
наконец, что число ±1 или 0 имеет две разные
записи, а это невозможно.
Наконец, докажем, что в минимальной
форме наименьшее количество ненулевых цифр
среди всех записей с отрицательными единицами.
Действительно, из любой записи можно с помощью
рассмотренных преобразований получить
построенную запись (как только что доказано,
всегда одну и ту же). Но при выполнении этих
преобразований величина v(a) не
возрастала, значит, построенная запись имеет
значение этой величины, равное наименьшему
возможному.
Преобразование обычной двоичной
записи числа a к минимальной форме более
удобно проводить следующим образом: вычислить
обычную двоичную запись 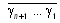 числа 3a и вычислить обычные разности числа 3a и вычислить обычные разности
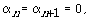 где i = 2, ..., n +
1, где i = 2, ..., n +
1, 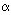 i —
цифры записи числа a, а i —
цифры записи числа a, а 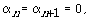 тогда тогда  —
минимальная форма числа a. —
минимальная форма числа a.
Минимальная форма максимум на единицу
длиннее обычной записи, но содержит не более n/2
ненулевых цифр. При смене знака у числа меняются
знаки у всех цифр его минимальной формы.
Действительно, при замене знаков всех цифр
минимальной формы числа a получается запись
числа –a, в которой нет двух ненулевых цифр
подряд. А это по определению и есть минимальная
запись числа –a.
Одно из возможных применений
указанной минимальной формы — уменьшение числа
арифметических операций для возведения в
степень. Мы уже приводили конкретный пример
такого применения, а сейчас сформулируем общую
теорему. Далее для краткости вместо
словосочетания “число арифметических операций
алгоритма” будем писать “сложность
алгоритма”.
Обозначим число ненулевых цифр в
записи числа n в виде минимальной формы через v(n),
а уменьшенную на единицу длину этой записи —
через 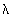 (n). Мы
используем те же обозначения, что и в обычном
бинарном методе (см. § 2), но заметим, что новая
функция (n). Мы
используем те же обозначения, что и в обычном
бинарном методе (см. § 2), но заметим, что новая
функция 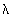 (n)
может быть на единицу больше старой, зато новая
функция v(n) не может быть больше старой, а
часто меньше ее, иногда почти в два раза. (n)
может быть на единицу больше старой, зато новая
функция v(n) не может быть больше старой, а
часто меньше ее, иногда почти в два раза.
 Теорема.
При использовании калькулятора с одной ячейкой
памяти сложность вычисления xn не
превосходит v(n) + Теорема.
При использовании калькулятора с одной ячейкой
памяти сложность вычисления xn не
превосходит v(n) + 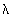 (n) – 1. (n) – 1.
Доказательство. Используя
полученную минимальную форму, запишем n в
виде суммы 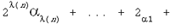 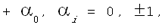 содержащей v(n)
ненулевых слагаемых. Далее, как и в обычном
бинарном методе возведения в степень, используем
аналог схемы Горнера, а цифрам –1 сопоставляем
операцию деления на основание степени.
Полученное обобщение бинарного метода
использует не более содержащей v(n)
ненулевых слагаемых. Далее, как и в обычном
бинарном методе возведения в степень, используем
аналог схемы Горнера, а цифрам –1 сопоставляем
операцию деления на основание степени.
Полученное обобщение бинарного метода
использует не более 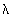 (n) возведений в квадрат и v(n)
– 1 умножений и делений. Теорема доказана. (n) возведений в квадрат и v(n)
– 1 умножений и делений. Теорема доказана.

Используя доказанное неравенство,
можно аналогично обычному бинарному методу в
случае, когда содержимое ячейки памяти 45 никогда
не обновляется, получить аналогичную нижнюю
оценку сложности возведения в степень v(n)
+ 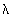 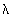 (n) – 1. Читателю
предоставляется возможность самому убедиться в
этом. (n) – 1. Читателю
предоставляется возможность самому убедиться в
этом.
Недостатком двоичной системы при ее
ручном использовании является то, что из-за
увеличения длины записи по сравнению с
десятичной системой соответственно возрастает и
сложность умножения. Использование минимальной
формы позволяет уменьшить сложность ручного
умножения двоичных чисел. Опишем алгоритм
умножения, предложенный в начале 1950-х годов
американским математиком Бутом.
Для этого данные n-разрядные и m-разрядные
двоичные числа преобразуем в их минимальные
формы и заметим, что эти формы содержат не более n
+ 1 и
m + 1 разрядов, причем из них не более a = n/2
+ 1 и b = m/2 + 1 ненулевых разрядов
соответственно. Сложность преобразования не
превосходит 3n + 3m – 4. Умножая минимальные
формы с помощью школьного алгоритма, замечаем,
что число нетривиальных умножений не
превосходит ab, так как ненулевых строк будет
не более b и в каждой из них нетривиальных
умножений не более a. Отметим, что каждое
нетривиальное умножение, по существу, не сложнее
нетривиального умножения в обычной двоичной
системе, и будем считать, что оно выполняется с
единичной сложностью, так же как и нетривиальное
сложение (операция нетривиальна, если оба
операнда не нули). Заметим также, что число
нетривиальных сложений не превосходит (b – 1)·(a
+ n – 1), так как всего сложений различных
строк требуется не более b – 1, а каждое из них
состоит из не более чем n переносов (переносы
могут быть как 1, так и –1) и не более чем a – 1
нетривиальных сложений (в складываемых строчках
имеется не более a – 1 стоящих друг под другом
ненулевых цифр). Поэтому сложность умножения не
превосходит (b – 1)·(a + n – 1) + ab 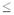 mn + (m + n)/2
+ 1. Полученный результат содержит не более n + m
+ 2 разрядов (так как он получается при сложении m
+ 1 не более чем (n + 1)-разрядных чисел с
соответствующими сдвигами). Его можно
преобразовать к обычной двоичной записи, сделав
не более n + m + 2 операции (заменяем блоки
соседних цифр вида 10...0 mn + (m + n)/2
+ 1. Полученный результат содержит не более n + m
+ 2 разрядов (так как он получается при сложении m
+ 1 не более чем (n + 1)-разрядных чисел с
соответствующими сдвигами). Его можно
преобразовать к обычной двоичной записи, сделав
не более n + m + 2 операции (заменяем блоки
соседних цифр вида 10...0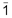 на соответствующие блоки вида 01...11,
блоки вида 1 на соответствующие блоки вида 01...11,
блоки вида 1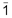 — на
блоки 01, блоки без отрицательных цифр оставляем
без изменения). Значит, полная сложность операции
умножения не превосходит mn + (m + n)/2 + 1 + 3n
+ 3m – 4 + n + m + 2 — на
блоки 01, блоки без отрицательных цифр оставляем
без изменения). Значит, полная сложность операции
умножения не превосходит mn + (m + n)/2 + 1 + 3n
+ 3m – 4 + n + m + 2 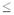 mn + 3,5(m + n). mn + 3,5(m + n).
§ 18. Быстроe умножение многочленов
Мало кто знает, что относительно
недавно были открыты гораздо более быстрые
алгоритмы умножения и деления многозначных
чисел и многочленов, чем “школьные”. Первый
такой алгоритм придумал в 1962 году А.А. Карацуба,
отвечая на вопрос А.Н. Колмогорова. Впоследствии
А.Л. Тоомом, Ф.Штрассеном и А.Шенхаге были
построены еще более быстрые алгоритмы.
Идею метода Карацубы можно пояснить на
следующем примере.

Эта формула сводит умножение
восьмизначных чисел к трем операциям умножения и
шести операциям сложения-вычитания
четырехзначных чисел (с учетом переносов в
следующие разряды). Обычный способ требует
четырех умножений и трех сложений-вычитаний, но
так как три раза сложить четырехзначные числа
можно быстрее, чем один раз перемножить, то метод
Карацубы уже восьмизначные числа перемножает
быстрее. В общем случае он требует для
перемножения n-значных чисел по порядку не
больше 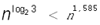 операций
над цифрами. операций
над цифрами.
Далее мы поговорим о сложности
умножения более подробно.
Обозначим через M(n) наименьшее
количество операций сложения, вычитания и
умножения (выполняемых над коэффициентами
многочленов и промежуточными числовыми
результатами), требующихся для перемножения двух
многочленов степеней, меньших n. Тогда
справедливо неравенство

нужно не более 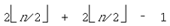 операций (так как число операций
равно наименьшему из количеств ненулевых
коэффициентов у складываемых многочленов), для
вычисления произведения (f1 + f0)(g1
+ g0) используется не более операций (так как число операций
равно наименьшему из количеств ненулевых
коэффициентов у складываемых многочленов), для
вычисления произведения (f1 + f0)(g1
+ g0) используется не более 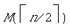 операций, для вычисления
разности (f1 + f0)(g1 + g0)
– f1g1 – f0g0
достаточно n – 1 операций, так как (f1
+ f0)(g1 + g0) – f1g1
– f0g0 = f1g0 + f0g1,
значит, степень этого многочлена равна операций, для вычисления
разности (f1 + f0)(g1 + g0)
– f1g1 – f0g0
достаточно n – 1 операций, так как (f1
+ f0)(g1 + g0) – f1g1
– f0g0 = f1g0 + f0g1,
значит, степень этого многочлена равна 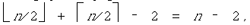 сложение
многочленов сложение
многочленов 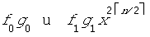 выполняется
“бесплатно”, так как они не имеют подобных
членов, причем в их сумме отсутствует член вида выполняется
“бесплатно”, так как они не имеют подобных
членов, причем в их сумме отсутствует член вида 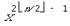 , поэтому для сложения
многочленов , поэтому для сложения
многочленов 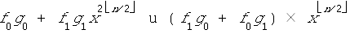 достаточно n – 2 операций. В итоге требуется
дополнительно
достаточно n – 2 операций. В итоге требуется
дополнительно 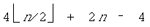 операций.
операций.
Оценку сложности метода Карацубы
можно представить в следующем виде. Если n
кратно 2k, то справедливо неравенство
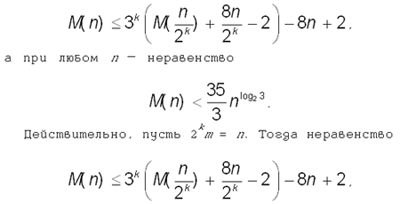 , ,
доказывается индукцией по k. База (k
= 1) — это неравенство (*). Шаг индукции
обосновывается тем же неравенством.
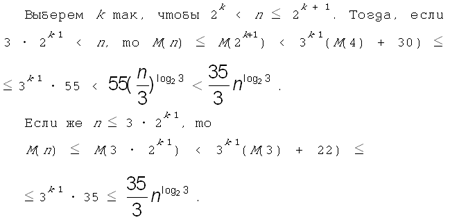
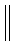 29.
Проверьте, что обычный способ умножения
многочленов дает оценку 29.
Проверьте, что обычный способ умножения
многочленов дает оценку
M(n) 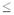 n2 + (n –
1)2. n2 + (n –
1)2.
§ 19. Быстроe умножение чисел
Перейдем теперь к умножению чисел.
Обозначим через M(n) наименьшее
количество операций сложения, вычитания и
умножения, выполняемых над числами, меньшими a,
требующихcя для перемножения двух n-значных
чисел, записанных в позиционной системе
счисления с основанием a.
Метод умножения почти такой же, как и
для многочленов.
Для примера укажем, как сделать
необходимые изменения в рассуждениях из
предыдущего параграфа.
Справедливы неравенства
M(2n) 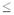 3M(n) + 19n, M(2n + 1) 3M(n) + 19n, M(2n + 1) 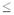 2M(n + 1) + M(n)
+ 17n + 10. 2M(n + 1) + M(n)
+ 17n + 10.
Действительно, применим тождество
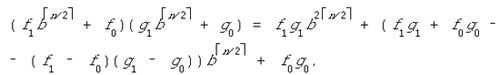
где числа f1 и g1 — 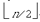 -разрядные, а числа f0
и g0 — -разрядные, а числа f0
и g0 — 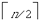 -разрядные
и заметим, что для вычисления произведений f1g1
и f0g0 требуется M( -разрядные
и заметим, что для вычисления произведений f1g1
и f0g0 требуется M(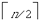 ) + M( ) + M(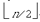 ) операций, для вычисления
разностей f0 – f1, g0 –
g1 и суммы f1g1 + f0g0
требуется не более n(1 + ) операций, для вычисления
разностей f0 – f1, g0 –
g1 и суммы f1g1 + f0g0
требуется не более n(1 + 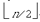 – – 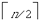 ) + 2( ) + 2(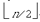 + + 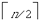 – 1) + 2( – 1) + 2(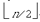 + + 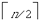 ) – 1 = 4n
– 3 + n(1 + ) – 1 = 4n
– 3 + n(1 + 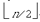 – – 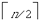 ) операций, так как
числа f1g1 и f0g0
имеют не более чем 2 ) операций, так как
числа f1g1 и f0g0
имеют не более чем 2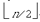 и 2 и 2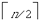 разрядов соответственно, а в случае четного n
нужно еще 2
разрядов соответственно, а в случае четного n
нужно еще 2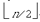 = n
операций для предварительного сравнения чисел
(чтобы не вычитать из меньшего большее). Заметим
далее, что для вычисления произведения (f1
– f0)(g1 – g0)
требуется не более M( = n
операций для предварительного сравнения чисел
(чтобы не вычитать из меньшего большее). Заметим
далее, что для вычисления произведения (f1
– f0)(g1 – g0)
требуется не более M(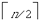 ) + 1 операций (одна операция для
вычисления знака у произведения), для вычисления
разности f1g1 + f0g0
– (f1 – f0)(g1 – g0)
= f1g0 + f0g1
требуется не более 2 ) + 1 операций (одна операция для
вычисления знака у произведения), для вычисления
разности f1g1 + f0g0
– (f1 – f0)(g1 – g0)
= f1g0 + f0g1
требуется не более 2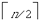 + 1 + 2 + 1 + 2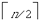 – 1 =
4 – 1 =
4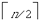 операций,
сложение чисел f0g0 и f1g1b2 операций,
сложение чисел f0g0 и f1g1b2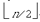 осуществляется
“бесплатно” (записи этих чисел просто
объединяются в одну запись), а для сложения чисел f1g1b2 осуществляется
“бесплатно” (записи этих чисел просто
объединяются в одну запись), а для сложения чисел f1g1b2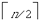 + f0g0
и (f1g0 + f0g1)b + f0g0
и (f1g0 + f0g1)b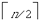 требуется не более 2n
– требуется не более 2n
– 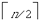 + n + 1 – 1 =
2n + + n + 1 – 1 =
2n + 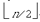 операций
(так как число f1g0 + f0g1
имеет не более n + 1 разрядов, а младшие лn/2ы
разрядов числа f0g0 не
участвуют в операциях). В итоге требуется
дополнительно 4n – 3 + + n(1 + операций
(так как число f1g0 + f0g1
имеет не более n + 1 разрядов, а младшие лn/2ы
разрядов числа f0g0 не
участвуют в операциях). В итоге требуется
дополнительно 4n – 3 + + n(1 + 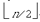 – – 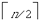 )
+ 1 + 4 )
+ 1 + 4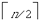 + 2n + + 2n + 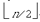 = 7n + 3 = 7n + 3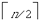 + n(1 + + n(1 + 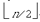 – – 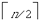 )
– 2 операций. )
– 2 операций.
Остальные детали предоставляем
додумать читателю.
Обозначим через Q(n) сложность
возведения n-разрядного числа в квадрат и
такое же обозначение будем использовать для
сложности возведения в квадрат многочлена
степени n – 1.
 30. Используя
тождество, докажите для случая операций с
числами неравенство M(n) 30. Используя
тождество, докажите для случая операций с
числами неравенство M(n) 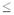 2Q(n) + 13n + O(1), а для
случая операций с многочленами — неравенство M(n) 2Q(n) + 13n + O(1), а для
случая операций с многочленами — неравенство M(n)
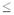 2Q(n) + 6n +
4. 2Q(n) + 6n +
4.
* Печатается по тексту одноименной книги.
Издательство МЦНМО, 2004.
Двумя чертами слева выделены тексты задач для
самостоятельного решения.
12 Разряды нумеруются с конца десятичной
записи. Например, 3-й разряд — это разряд сотен.
13 Через 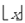 обозначается наибольшее целое число, не
большее x (“округление вниз”), а через обозначается наибольшее целое число, не
большее x (“округление вниз”), а через 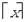 — наименьшее целое
число, не меньшее x (“округление вверх”). — наименьшее целое
число, не меньшее x (“округление вверх”).
|