В мир информатики # 90 (16–30 апреля).
Семинар
Системы счисления1
Verba volent, scripta manen.
Слова улетают, написанное остается.
(лат.)
Мысль выражать все числа немногими
знаками, придавая им, кроме значения по форме, еще
значение по месту, настолько проста, что именно
из-за этой простоты трудно оценить, насколько она
удивительна.
Пьер Симон Лаплас
Ключевые числа
Первые девять натуральных чисел мы
обозначаем специальными знаками:
1, 2, 3, 4, 5, 6, 7, 8, 9.
Поступать таким же образом со всеми
встречающимися на практике числами было бы
неудобно. Даже если бы наши потребности
ограничивались счетом в пределах тысячи, надо
было бы запомнить тысячу специальных знаков.
Естественно, что уже давно люди стали выбирать
тот или иной ряд “ключевых”, основных чисел и
только их обозначать специальными знаками.
Такова, например, римская система счисления
(нумерация), основанная на ключевых числах 1, 5, 10,
50, 100, 500, 1000. Эти числа в римской системе счисления
обозначают буквами I (“и”), V (“в”), X (“икс”), L
(“эль”), С (“це”), D (“де”) и М (“эм”).
Такие обозначения частично произошли
от рисунков, изображавших некогда
соответствующие числительные (I — палец, V —
пятерня с расставленными пальцами, X — две
пятерни):

а частично являются сокращениями
латинских слов (centum — сто, demimille —
пятьсот, mille — тысяча).
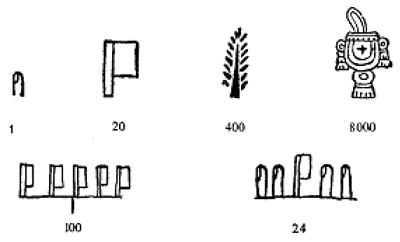
Числовые знаки ацтеков
Так как римская система нумерации
нужна нам только для примера, мы рассмотрим ее в
более древнем, упрощенном, варианте, когда число
“четыре” писалось в виде IIII, а не в виде IV. Число
3477 в этой староримской системе записывается так:
MMMCCCCLXXVII = 3 · 1000 + 4 · 100 + 50 + 2 · 10 + 5 + 2.
Аналогично поступает кассир, имеющий
денежные купюры достоинством в 100 рублей, 50
рублей, 10 рублей и монеты достоинством 5 рублей, 2
рубля и 1 рубль. Для кассира ключевыми являются
числа
100, 50, 10, 5, 2 и 1.
Желая выплатить, скажем, 496 рублей, он
выдает сначала столько сотенных бумажек, сколько
возможно, чтобы не выдать лишнего:
496 = 4 · 100 + 96
Затем он выдает столько купюр по 50
рублей, сколько возможно, чтобы выдать не более
оставшихся к выплате 96 рублей:
496 = 4 · 100 + 1 · 50 + 46,
и т.д. Иногда у него может получиться
остаток меньше, чем следующее ключевое число. Так
будет в нашем примере после выдачи пяти рублей:
496 = 4 · 100 + 1 · 50 + 4 · 10 + 1 · 5 + 1.
Следующее ключевое число равно 2,
однако так как 1 < 2, то двухрублевые монеты
выдавать не придется. Но для полноты картины
можно считать, что было выдано 0 двухрублевых
монет, и включить в сумму слагаемое 0 · 2. Вся
процедура выдачи 496 рублей запишется так:
496 = 4 · 100 + 1 Ч 50 + 4 · 10 + 1 · 5 + 0 · 2 + 1 · 1.
Попробуем теперь обобщить сказанное,
взяв в качестве последовательности ключевых
чисел (“базиса”) любую последовательность
возрастающих натуральных чисел:
q0 = 1 < q1 < q2
< … qn < … (1)
Опишем, как получить запись
произвольного числа N в системе счисления с
базисом (1).
В последовательности (1) ключевых чисел
находим самое большое число qn, не
превосходящее N. Делим N на qn и
получаем (неполное) частное an и остаток rn
– 1:
N = anqn + rn
– 1, где 0 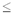 rn-1
< qn. rn-1
< qn.
Первый остаток rn-1 делим (с
остатком) на следующее ключевое число qn-1.
Получаем
rn-1 = an-1qn-1
+ rn-2, где 0 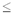 rn-2 < qn-1, rn-2 < qn-1,
или
N = anqn + an-1qn-1
+ rn-2.
(Заметьте, что мы не исключаем здесь и
тот случай, когда rn-1 = 0, — в этом случае
все последующие частные и остатки будут равны
нулю!)
Теперь опять новый остаток rn-2
делим на qn-2 и получаем:
rn-2 = an-2qn-2
+ rn-3, где 0 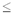 rn-2 < qn-2, rn-2 < qn-2,
или N = anqn +
an-1qn-1 + an-2qn-2
+ rn-3,
и т.д.
В конце концов, разделив предпоследний
остаток r1 на q1, получаем:
N = anqn + an-1qn-1
+ … + a2q2 + a1q1
+ r0,
где 0 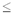 r0
< q1. r0
< q1.
(Так как q0 = 1, то делить на
него “последний остаток” r0 излишне:
ясно, что r0 = a0q0 = a0.)
Практически подобное многократное
деление обычно записывают слитно. Как это
делается, мы покажем на уже разобранном примере
записи суммы в 496 рублей в “системе кассира” (cм.
таблицу).
(Здесь все частные an, an-1
и т.д. оформлены жирным начертанием, а само
число N и остатки rn-1, rn-2 и
т.д. — курсивом.)
Позиционные системы счисления
Вероятно, вы уже догадались, что в
случае базиса
q0 = 1, q1 = 10, q2
= 102, …, qn = 10n
мы будем иметь дело с десятичной системой
счисления, которую мы используем в повседневной
жизни (не считая уроков информатики — :). Но
вместо того чтобы писать, скажем, 4 · 105 + 0 · 104
+ 3 · 103 + 0 · 102 + 1 · 10 + 7, мы пишем просто
403017.
Рассеянный или чересчур пунктуальный
кассир мог бы приготовить для записи своих выдач
ведомость, где число выданных купюр разного
достоинства заносилось бы в отдельные столбцы. В
такой ведомости выдача 496 рублей выглядела бы
так:

Можно сказать, что в “системе
счисления кассира” число 496 записывается в виде
414101.
Системы счисления, родственные
разобранным в последних двух примерах (т.е.
десятичной системе счисления и “системе
кассира”), называются позиционными (о
значении этого выражения мы еще скажем ниже).
Вместо громоздкой записи
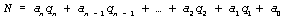
в позиционной системе счисления с
базисом (1) удобно пользоваться более компактной
записью из n + 1 “цифры”:
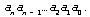
При этом предполагается, что
“цифры” ak получены тем способом
(алгоритмом), который был описан выше.
Из этого описания ясно, что в заданном
базисе каждое натуральное число N записывается
единственным образом. Далее, так как “старшая
цифра” an получается как частное от
деления на qn числа N, которое по
условию меньше qn+1 (ибо иначе мы начали
бы с деления N на qn+1, а не на qn),
то an < qn+1/qn. Поэтому,
если частное qn+1/qn заключено между
целыми числами А и А – 1:
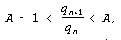
“цифра” an не превосходит А
– 1, т.е. она может принимать А значений: 0,
или 1, или 2, ..., или А – 1. (Впрочем, для
“старшей” цифры числа значение
an = 0 также можно исключить.)
Аналогично цифра an-1 получается
в процессе деления “первого” остатка rn-1
на qn-1.
Но так как 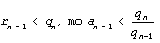 . .
Это рассуждение можно распространить
и на все другие цифры. В частности, так как
последняя цифра a0 просто совпадает с
“последним” остатком r0, полученным
при делении на q1, то a0
может принимать q1 значений: 0, или 1,
или 2, ..., или q1 – 1.
До позиционной системы счисления люди
дошли не сразу. Одним из затруднений долго было
отсутствие числа “нуль” (и специального знака
для этого числа). Впервые знак нуля появился в
рамках вавилонской шестидесятеричной системы
счисления.
В вавилонских текстах, написанных характерной
“клинописью” (см. рисунок ниже), числа от 1 до 59
записывались по десятичной системе.
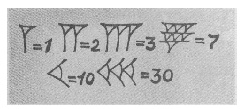
Но основной для вавилонской
математики была шестидесятеричная система
счисления с базисом
1, 60, 602, 603, …, 60n, …
До мысли иметь специальный знак нуля
математики, пользовавшиеся клинописью, дошли
довольно поздно (впрочем, заведомо не позднее
третьего века до нашей эры). Знак нуля выглядел
так:

Вы поймете после этих разъяснений, что
запись:

означает число 2 593 292 = 12 · 603
+ 0 · 602 + 21 · 60 + 32.
Очень близка к вавилонской система
счисления, принятая в древней цивилизации
индейцев майя, обитавших на территории
Центральной Америки. Создание этой системы
счисления относится к началу нашей эры. Если
вавилонская система счисления имела
комбинированный десятично-шестидесятеричный
характер, то система майя была
пятерично-двадцатеричной2. Первые 19 чисел
записывались комбинированием черточки,
обозначавшей пятерку, и точки (единицы):
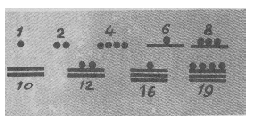
Но основную роль играла искаженная
двадцатеричная система счисления. При записи
числа “цифры” подписывались одна под другой,
причем старшей являлась верхняя цифра.
Прилагательное “искаженная” означает вот что:
третье — после 1 и 20 — ключевое число в системе
майя равнялось не 20 · 20 = 202, а 18 · 20 = 360; далее
шли 18 · 202, 18 · 203, 18 · 204.
Существовало и специальное обозначение для нуля,
напоминающее полузакрытый глаз:
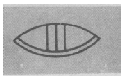
Вот несколько примеров записи чисел в
системе майя:
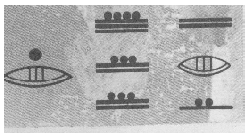
(1 · 20 + 0 = 20, 19 · 360 + 13 · 20 + 13 = 7113, 10 · 360 + 0 ·
20 + 7 = 3607).
Основное отличие записи чисел в
вавилонской системе счисления и в системе майя
от римской нумерации как раз и заключается в
“позиционном” принципе этих систем: в то время
как у римлян буква I всегда означает единицу, а V —
пятерку, независимо от того, где эти буквы стоят,
у древних вавилонян и у индейцев майя значение
“цифры” существенно зависит от занимаемого ею
места, или “позиции”. Именно поэтому такие
системы записи чисел (к числу которых
принадлежит и десятичная система, созданная в
Индии в VIII—IX вв. или немного раньше) называют позиционными.
Задания для самостоятельной работы
1. Запишите в “полной системе кассира”
(где “ключевыми” являются следующие числа:
100 000, 50 000, 10 000, 5000, 1000, 500, 200, 100, 50, 10, 5
и 1, отвечающие выраженным в копейках ценностям
всех существующих бумажных денег и всех монет)
сумму в 233 руб. 87 коп. Запишите операцию перевода 23
387 коп. в “систему кассира” с помощью
“непрерывного деления” (см. выше).
2. Прочтите записанное по вавилонской
системе число

3. Прочтите записанное по системе майя
число

(Это самое большое число, обнаруженное
в памятниках культуры майя.)
1 При подготовке статьи использовались
материалы статьи с аналогичным названием,
опубликованной в журнале “Квант” в 1970 г. (автор
— доктор физико-математических наук И.Яглом).
2 Обращаем внимание на написание названий
систем: пятеричная, двадцатеричной,
шестнадцатеричная и т.п. |