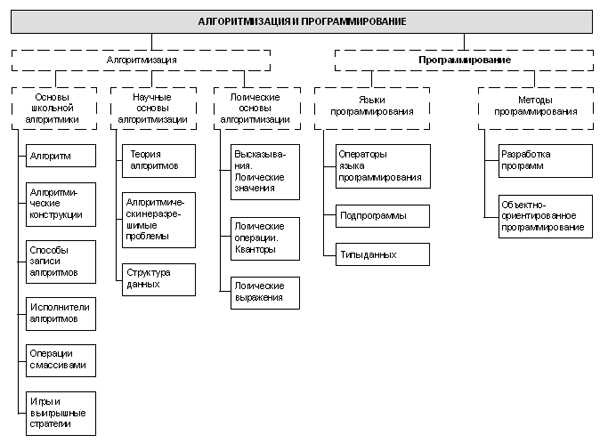
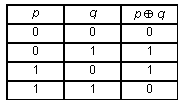
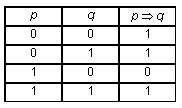
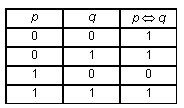
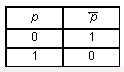
ЭНЦИКЛОПЕДИЯ УЧИТЕЛЯ ИНФОРМАТИКИV. Алгоритмизация и программированиеСписок статей1. Алгоритм 2. Алгоритмически неразрешимые проблемы 3. Алгоритмические конструкции 4. Высказывания. Логические значения 5. Игры и выигрышные стратегии 6. Исполнители алгоритмов 7. Логические выражения 8. Логические операции. Кванторы 9. Объектно-ориентированное программирование 10. Операторы языка программирования 11. Операции с массивами 12. Подпрограммы 13. Разработка программ 14. Способы записи алгоритмов 15. Структуры данных 16. Теория алгоритмов 17. Типы данных 18. Языки программирования Школьная информатика в России начиналась с алгоритмизации и программирования, как с основной темы курса. Эта тема изучалась и в безмашинном варианте, и с компьютерной поддержкой на БК и Yamaha — компьютерах, первыми появившимися в школах. Основным программным обеспечением данных компьютеров был встроенный язык программирования Бейсик. С развитием школьной информатики как самостоятельного предмета круг тем, рассматриваемых этим предметом, существенно расширился и алгоритмизация стала лишь одной из них, а относительно программирования в Стандарт основной школы включена фраза “Представление о программировании”. Полностью тема программирования включена лишь в Стандарт профильной школы. Тем не менее в Примерной программе программированию уделено заметное место. Там указаны следующие темы для рассмотрения: языки программирования, их классификация; правила представления данных; правила записи основных операторов: ввода, вывода, присваивания, ветвления, цикла; правила записи программы; этапы разработки программы: алгоритмизация — кодирование — отладка — тестирование. В программу включен также большой объем практических работ по программированию. Вопросы по программированию входят практически в каждый экзаменационный билет по информатике для 11-го класса. Более 30% баллов ЕГЭ по информатике приходятся на вопросы по данной теме, а с учетом логики, включенной в последнем варианте стандарта в этот же раздел, — более 40%. А различные этапы Всероссийской олимпиады по информатике — от первого школьного этапа до пятого заключительного — фактически представляют собой олимпиады по алгоритмизации и программированию. Программирование традиционно относят к сложным темам школьного курса информатики, признавая при этом, что именно решение задач по теме алгоритмизация и программирование в максимальной степени способствуют развитию алгоритмического стиля мышления, который формирует общеучебные навыки. Действительно, для успешного решения задачи, требующей составления алгоритма и написания программы, ученик должен: 1) четко понять задачу, провести ее детализацию и формализацию; 2) проанализировать, к какому классу задач она относится, какими способами (алгоритмами) ее можно решить; 3) составить алгоритм решения задачи; 4) составить программу, реализующую этот алгоритм; 5) проверить, правильно ли программа работает, ту ли задачу она решает; 6) в случае обнаружения ошибки необходимо проделать все (или некоторые) вышеперечисленные действия заново с целью исправления ошибки. Когнитивный анализ выполнения учебных задач показывает, что аналогичным способом решаются задачи по математике и физике, пишутся рефераты и доклады по любому школьному предмету. Кроме того, все эти действия мы выполняем каждый раз, когда решаем сложные бытовые проблемы (например, ремонт в квартире), организационные проблемы (школьный поход) и т.д. Изучение данной темы, бесспорно, начинается с понятия алгоритма. Это понятие рассматривается, начиная с пропедевтического курса информатики в начальной школе и заканчивая формальным определением алгоритма, формулируемым в профильных классах старшей школы при изучении основ теории алгоритмов. Кроме данного определения, в Стандарте упомянуты такие темы теории алгоритмов, как вычислимая функция, сложность алгоритмов, алгоритмически неразрешимые проблемы и ряд других достаточно сложных тем и понятий, ранее в школьной информатике не рассматривавшихся. Понятие алгоритма рассматривается совместно с понятием исполнителя и его системы команд. Способы записи алгоритмов неотделимы от такого понятия, как алгоритмические конструкции. При изучении алгоритмических конструкций необходимо сделать акцент на то, что представление любого алгоритма возможно с помощью композиции трех базовых структур (следование, ветвление, цикл). Понимание этого факта позволяет осмысленно использовать метод структурного программирования. Использование таких алгоритмических конструкций, как ветвление и цикл, подразумевает использование логических выражений, построение которых невозможно без понятия высказывания, логического значения, логических операций и кванторов. Алгоритм, представленный в форме, пригодной для восприятия и выполнения компьютером, называется программой. Для записи алгоритмов в такой форме существуют различные языки программирования. Алгоритмические конструкции в языке программирования записываются с помощью соответствующих операторов. Информация, подаваемая на вход программе, называется данными. Одной из задач информатики является нахождение форм представления информации, удобных для компьютерной обработки. Информатика, как точная наука, работает с формальными (описанными математически строго) структурами данных. Примерами структур данных являются числа, логические значения, последовательности, таблицы, строки, списки, деревья, графы и т.п. Перечисленные структуры данных существуют независимо от их реализации в программировании. С этими структурами работали математики и в XVIII, и в XIX веках, когда еще не придумали вычислительные машины и никто не знал, что наступит эра информатизации. Удачный выбор структуры данных для представления информации может существенно повысить эффективность решения задачи. Реализация этих структур в языке программирования производится через соответствующие типы данных. В школьном курсе информатики изучаются различные алгоритмы, связанные с обработкой наиболее распространенных структур данных, и если речь идет об изучении языка программирования, то в первую очередь изучаются операции с массивами. Это и поиск максимального или минимального элемента, и сортировка элементов массива в определенном порядке, и ряд других алгоритмов. В Стандарте для профильных классов средней школы упоминается и такая тема, как игры и выигрышные стратегии.
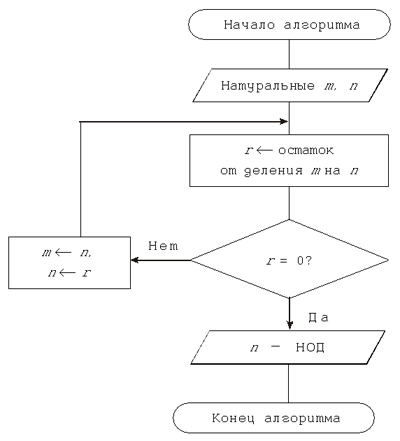
Система статей раздела “Алгоритмизация и программирования” Разработка программ в настоящее время — это достаточно сложный процесс, она требует и знания систем программирования, и владения технологией программирования, и сознательного использования одной из парадигм программирования, в частности, объектно-ориентированного программирования. Тема “Алгоритмизация и программирование” изучается на всех ступенях средней школы, но на разном уровне. В начальной школе происходит знакомство на интуитивном уровне с понятиями алгоритма, алгоритмических конструкций, основ алгебры логики. В качестве учебных задач рассматривают бытовые, игровые, сказочные алгоритмы. В средних классах школы в рамках данной темы происходит уточнение понятия алгоритма, основы алгебры логики излагаются на более формальном уровне. При решении учебных задач учащиеся знакомятся с разными способами записи алгоритмов, изучают свойства алгоритма, рассматривают некоторые алгоритмы (алгоритм Евклида, сортировка данных и т.д.). В старших классах, и особенно в классах физико-математического, информационно-технологического профилей, изучение этой темы строится в соответствии со Стандартом. Успешность учащихся в освоении этой темы во многом зависит от приобретенных ими общеучебных навыков в предыдущие годы обучения. Без сомнения, навыки, составляющие основу алгоритмического мышления, должны формироваться, начиная с младших классов. 1. АлгоритмЧто такое алгоритмПонятие алгоритма, являющееся фундаментальным понятием математики и информатики, возникло задолго до появления вычислительных машин. Первоначально под словом алгоритм понимали способ выполнения арифметических действий над десятичными числами. В дальнейшем это понятие стали использовать для обозначения любой последовательности действий, приводящей к решению поставленной задачи. Само же слово алгоритм появилось в Средние века, когда европейцы познакомились со способами выполнения арифметических действий, описанными узбекским математиком Мухаммедом бен Муса аль-Хорезми. Слово алгоритм — европеизированное произношение слов аль-Хорезми. В своем нынешнем смысле слово алгоритм часто ассоциировалось с алгоритмом Евклида, который представляет собой процесс нахождения наибольшего общего делителя (НОД) двух чисел. Приведем современное описание алгоритма Евклида с использованием блок-схемы (см. “Способы записи алгоритмов”): Стрелка “
Любой алгоритм существует не сам по себе, а предназначен для определенного исполнителя (см. “Исполнители алгоритмов”). Алгоритм описывается в командах исполнителя, который этот алгоритм будет выполнять. Объекты, над которыми исполнитель может совершать действия, образуют так называемую среду исполнителя, а множество команд, которые исполнитель может выполнять, — систему команд исполнителя (СКИ). Таким образом, алгоритм можно рассматривать как последовательность команд управления работой исполнителя (предписание исполнителю на выполнение последовательности действий). Свойства алгоритмаЗначение слова алгоритм очень схоже со значением слов рецепт, инструкция. Однако любой алгоритм в отличие от рецепта или способа обязательно обладает следующими свойствами. 1. Выполнение алгоритма разбивается на последовательность законченных действий-шагов. Только выполнив одно действие (команду), можно приступать к исполнению следующего. Это свойство алгоритма называется дискретностью. Произвести каждое отдельное действие исполнителю предписывает специальное указание в записи алгоритма (команда). 2. Понятность — алгоритм не должен содержать предписаний, смысл которых может восприниматься исполнителем неоднозначно, т.е. запись алгоритма должна быть настолько четкой и полной, чтобы у исполнителя не возникало потребности в принятии каких-либо самостоятельных решений. Алгоритм всегда рассчитан на выполнение “не размышляющего” исполнителя. Алгоритм составляется из команд, входящих в СКИ.
Рассмотрим известный пример “бытового” алгоритма — алгоритм перехода улицы: “Посмотри налево. Если машин нет, дойди до середины улицы. Если есть, подожди, пока они проедут, и т.д.”. Представьте себе ситуацию: машина слева есть, но она не едет — у нее меняют колесо. Если вы думаете, что исполнитель алгоритма должен ждать, то вы поняли этот алгоритм. Если же вы решили, что улицу переходить можно, считая алгоритм подправленным ввиду непредвиденных (по вашему мнению!) обстоятельств, то вы не усвоили понятие алгоритма.
3. Детерминированность (определенность и однозначность). Каждая команда алгоритма определяет однозначное действие исполнителя, и должно быть однозначно определено, какая команда выполняется следующей. То есть если алгоритм многократно применяется к одному и тому же набору исходных данных, то на выходе он получает каждый раз один и тот же результат. 4. Результативность — исполнение алгоритма должно закончиться за конечное число шагов, и при этом должен быть получен результат решения задачи. В качестве одного из возможных результатов может быть и установление того факта, что задача решений не имеет. Свойство результативности содержит в себе свойство конечности — завершение работы алгоритма за конечное число шагов. 5. Массовость — алгоритм пригоден для решения любой задачи из некоторого класса задач, т.е. алгоритм правильно работает на некотором множестве исходных данных, которое называется областью применимости алгоритма. Свойство массовости определяет скорее качество алгоритма, а не относится к обязательным свойствам (как дискретность, понятность и пр.). Существуют алгоритмы, область применимости которых ограничивается единственным набором входных данных или даже отсутствием таковых (например, получение фиксированного числа верных цифр числа p). Правильнее говорить о том, что алгоритм должен быть применим к любым данным из своей области определения, и слово массовость не всегда подходит для описания такого свойства. Понятие алгоритмаОбобщив вышесказанное, сформулируем следующее понятие алгоритма. Алгоритм — понятное и точное предписание исполнителю на выполнение конечной последовательности действий, приводящей от исходных данных к искомому результату. Приведенное определение не является определением в математическом смысле слова, т.е. это не формальное определение (формальное определение алгоритма см. в статье “Теория алгоритмов”). Отметим, что для каждого исполнителя набор допустимых действий (СКИ) всегда ограничен — не может существовать исполнителя, для которого любое действие является допустимым. Перефразированное рассуждение И.Канта обосновывает сформулированное утверждение следующим образом: “Если бы такой исполнитель существовал, то среди его допустимых действий было бы создание такого камня, который он не может поднять. Но это противоречит допустимости действия «Поднять любой камень»”. Интересно, что существуют задачи, которые человек, вообще говоря, умеет решать, не зная при этом алгоритм ее решения. Например, перед человеком лежат фотографии кошек и собак. Задача состоит в том, чтобы определить, кошка или собака изображена на конкретной фотографии. Человек решает эту задачу, но написать алгоритм решения этой задачи пока чрезвычайно сложно. С другой стороны, существуют задачи, для которых вообще невозможно построить процедуру решения. Причем данный факт можно строго доказать. Об этом вы можете прочитать в статье “Алгоритмически неразрешимые проблемы” 2. Методические рекомендацииДанная тема традиционно изучается в базовом курсе информатики основной школы. Содержание статьи “Алгоритм” может рассматриваться в качестве базового минимума информации по этой теме для учеников 8–9-х классов. В пропедевтическом курсе информатики (5–7-е классы) более актуальным является составление конкретных алгоритмов с использованием различных форм их записи, в том числе и для учебных исполнителей (см. “Исполнители алгоритмов”). Каждый из нас ежедневно решает задачи различной сложности: как быстрее добраться в школу или на работу в условиях нехватки времени; в каком порядке выполнять дела, намеченные на текущий день, и т.д. Некоторые задачи настолько сложны, что требуют длительных размышлений для нахождения решения (иногда решение так и не удается найти), другие задачи мы решаем автоматически, так как выполняем их ежедневно на протяжении многих лет (почистить утром зубы; позвонить другу по телефону). В большинстве случаев решение каждой задачи можно подразделить на простые этапы. Пример. Задача “Звонок другу по телефону” подразделяется на следующие этапы (шаги): 1. Поднять телефонную трубку. 2. Если услышал гудок, то набрать номер друга, иначе конец решения задачи с отрицательным результатом (телефон неисправен). 3. Определить тип гудков: “вызов” или “занято”. Если “вызов”, перейти к шагу 4, если “занято”, перейти к шагу 6. 4. Дождаться 6 вызывающих гудков (конкретное число гудков в алгоритме для разных людей может быть различным). 5. Если за это время абонент не поднял трубку, то конец решения задачи с отрицательным результатом (абонент не отвечает). Иначе начать разговор (задача решена успешно). 6. Положить телефонную трубку; конец решения задачи с отрицательным результатом (абонент занят).
Последовательность шагов, приведенная в примере 1, является алгоритмом решения задачи “Звонок другу по телефону”. Исполнитель этого алгоритма — человек. Объекты алгоритма — телефон и телефонные сигналы. При разборе алгоритма “Звонок другу по телефону” следует обратить внимание на п. 4 (“дождаться 6 вызывающих гудков”): без указания конкретного числа гудков нарушается сразу несколько свойств алгоритма (дискретность, определенность и результативность). Естественно, вместо числа 6 в алгоритме может стоять любое другое разумное число. Для решения любой задачи надо знать, что дано и что следует получить, т.е. у задачи есть исходные данные (некие объекты) и искомые результаты. Для получения результатов необходимо знать способ решения задачи, то есть располагать алгоритмом, в котором указано, какие действия и в каком порядке следует выполнить, чтобы решить задачу (получить искомые результаты). Далее следует разобрать свойства алгоритма на примере решения какой-либо бытовой проблемы. Составление алгоритмов для решения бытовых проблем только на первый взгляд кажется простым, мы очень многие действия делаем автоматически, и их формализация требует от учащихся учета многих деталей и факторов. При изложении теоретического материала необходимо обратить внимание на то, почему приведенное определение алгоритма не является строгим математическим определением, а является только описанием понятия алгоритм, раскрывающим его сущность. Оно не является формальным потому, что в нем используются такие не уточняемые понятия, как “система правил”, “исходные данные”, и т.д. В рамках изучения этой темы желательно также обсудить вопрос, является ли способ переправки Волка, Козы и Капусты через реку алгоритмом (эта задача рассматривается во многих учебниках информатики как пример задачи на построение алгоритмов)? Иногда ученики сначала склоняются к мнению, что решение упомянутой задачи алгоритмом не является, т.к. не обладает свойством массовости. Но способ решения частной задачи — это тоже алгоритм (см. замечания о массовости в тексте статьи). Стоит отметить, что областью применимости данного конкретного алгоритма являются все наборы объектов, которые характеризуются теми же взаимоотношениями, что и Волк, Коза и Капуста. Например, Удав, Кролик и Морковка. Иногда вызывает споры и свойство конечности алгоритма. В качестве контрпримеров приводятся алгоритмы работы операционной системы и атомной электростанции. Не углубляясь в спор, заметим, что здесь делается попытка представить алгоритм, в котором в качестве исходного объекта рассматривается компьютер, обладающий непрерывными свойствами (бесконечная бесперебойная работа вне зависимости от действий пользователя и проблем с “железом”). Алгоритмы же работают по определению только с дискретными объектами (см. статью “Теория алгоритмов”). Кроме того, свойство конечности существенно при доказательстве ряда фундаментальных утверждений в теории алгоритмов (см., например, “Алгоритмически неразрешимые проблемы”), поэтому опускать его даже в рамках базового курса информатики не следует. Важным при изучении данной темы является и понятие исполнителя. Причем оказывается, что гораздо проще построить алгоритм для программно-управляемого автомата (в том числе компьютера), чем для человека. Подробнее об этом рассказано в статье “Исполнители алгоритмов” 2. Для управления автоматом или компьютером можно придумать формальный язык описания алгоритмов. Такие языки называются “Языки программирования” 2, а сам алгоритм, записанный на таком языке, — программой. При изучении данной темы полезным оказывается построение алгоритмов, известных ученикам из курса математики, но записываемых в математике менее формально. Например, алгоритм решения квадратного уравнения (в информатике более полезно решать обобщенно-квадратное уравнение, в котором коэффициент при x2 может быть равен 0), алгоритм решения задач на построение (здесь особое внимание следует уделять детерминированности алгоритма) и т.п. В курсе информатики средней школы к понятию алгоритма можно вернуться в контексте изучения темы “Моделирование” 2. Ведь алгоритм можно рассматривать как информационную модель деятельности исполнителя. В профильном курсе информатики углубление данной темы происходит в результате знакомства с основами “Теории алгоритмов” 2, в рамках которой в первую очередь дается уже формальное определение алгоритма. 2. Алгоритмически неразрешимые проблемыМатематики в течение веков пользовались интуитивным понятием алгоритма (см. “Алгоритм”). В рамках подобного определения были сформулированы и успешно применялись на практике алгоритмы для решения таких задач, как выполнение арифметических действий “столбиком”, нахождение корней квадратных уравнений, решение систем линейных уравнений и т.д. Постепенно они переходили к постановке и решению все более сложных задач. Так, Г.Лейбниц в XVII веке пытался построить общий алгоритм решения любых математических задач. В XX веке эта идея приобрела более конкретную форму: построить алгоритм проверки правильности любой теоремы при любой системе аксиом. Построить такие алгоритмы не удавалось, и математики выдвинули предположение: а вдруг для того или иного класса задач в принципе невозможно построить алгоритм решения? На основе этого предположения возникло понятие алгоритмически неразрешимой задачи — задачи, для которой невозможно построить процедуру решения.
Проблема остановаОдной из первых проблем, для которых была строго доказана алгоритмическая неразрешимость, была так называемая проблема останова. Сформулируем ее для программ, написанных на процедурных языках программирования (см. “Языки программирования”). Зададимся следующим вопросом. Нельзя ли определить программным способом, с помощью самого компьютера, зациклится ли данная программа на определенных входных данных? Может быть, можно написать некоторую универсальную программу (обозначим ее через U), которая принимала бы на вход текст заданной программы и входные данные к ней, анализировала его и выдавала бы ответ, зациклится эта программа на этих входных данных или нет1. Возможность написания программы U кажется правдоподобной: ведь, например, программа-компилятор умеет анализировать текст заданной программы на наличие в нем возможных синтаксических ошибок и т.п. Программа U могла бы стать надстройкой над компилятором, которая вылавливала бы ошибку особого рода — ошибку “бесконечного цикла”. Уточним формулировку задачи. Каждая
программа П в каждом конкретном случае
работает с входными данными. (Строго говоря,
некоторые программы, например программа
вычисления числа Работу программы U можно спроектировать следующим образом. Программа U должна получать на вход, во-первых, текст программы П (текстовый файл), а во-вторых, некоторый файл с данными Д (текстовый файл). Затем она должна проанализировать эти два файла и выдать точный ответ: зациклится ли программа П, если П получила на вход файл Д. Можно всегда считать, что программа U может воспринимать на вход любые файлы: например, если файл П не является синтаксически правильной программой на выбранном языке программирования (скажем, Паскале), то программа U это легко определяет, но все равно считает, что в этом случае П является “программой”: например, такой, которая “ничего не делает” и, следовательно, не зацикливается. Соответственно, если файл Д имеет “неправильный формат” (например, на вход программе П требуется число, а в файле Д имеется что-то другое), то программа П всегда останавливается на этих “неправильных данных”. Итак, вот более точное описание программы U: а) программа U читает два произвольных файла: П и Д; б) если файл П содержит синтаксически правильную программу (для определенности, на Паскале), а файл Д представляет собой корректные данные для программы П, то программа U проверяет, зациклится ли П на данных Д. Если она зациклится, то на экран компьютера будет выдано сообщение “зациклится”, иначе — “не зациклится”; в) если файлы П и Д не удовлетворяют условиям б), то на экран выдается сообщение “не зациклится” (и в этой ситуации для простоты мы все равно называем П программой, а Д — данными, и П в этом случае не зацикливается на Д “по определению”). Предположим, что нам удалось написать такую программу U. Можно считать, что она тоже написана на Паскале. Теперь мы собираемся написать новую программу, которую обозначим через U1. Но прежде мы введем специальное понятие — стандартный номер файла. Любой файл можно представить как слово, быть может, очень длинное. Каждая “буква” этого слова берется из некоторого алфавита. Например, можно считать, что алфавит для таких слов состоит из 256 символов, а каждая буква в слове — это один байт в файле; в качестве “букв” здесь выступают все ASCII-символы — “настоящие буквы”, знаки препинания, пробел, специальные символы и т.д. Таким образом, все файлы могут быть расположены в некоторую упорядоченную бесконечную последовательность: Ф0, Ф1, Ф2, Ф3, ... (*) (Сначала идет пустой файл Ф0, в котором нет ни одного байта. Затем перечисляются в алфавитном порядке все файлы, состоящие из одной “буквы”, затем — состоящие из двух “букв”, и т.д.) В этой последовательности каждый файл получает некоторый номер. Этот номер мы и назовем стандартным номером файла. Ясно, что можно написать программу, которая по заданному файлу вычислит стандартный номер этого файла. (Мы считаем, что у нас есть “идеальный” компьютер. Он не имеет ограничений памяти и поэтому может работать с числами, состоящими из сколь угодно большого количества цифр.) Можно также написать программу, которая по заданному числу восстанавливает файл, стандартный номер которого равен n. Итак, любой файл попадает в последовательность (*) и имеет в ней свой уникальный номер, который мы называем стандартным номером этого файла. Значит, и у любого файла с программой (П), и у любого файла данных (Д) есть свои стандартные номера. Теперь можно написать программу U1, которая будет делать следующее: 1) получать на вход натуральное число i; 2) восстанавливать файл Фi из последовательности (*), т.е. восстанавливать файл со стандартным номером i; 3) запускать программу U, подавая ей на вход в качестве файла П файл Фi, а в качестве файла Д — тот же самый файл Фi. Коротко работу программы U1 можно описать так: по заданному числу i она определяет, зациклится ли программа, реализованная в файле со стандартным номером i при работе с данными, записанными в файле, который имеет стандартный номер i (эта программа решает проблему самоприменимости). Ясно, что программу U1 всегда можно написать так, чтобы она в самом конце работы некоторой переменной z присваивала значение 0 или 1, и в соответствии с этим значением выводила одно из двух сообщений: if z = 0 then writeln('нe зациклится') else writein('зациклится') Теперь подвергнем программу U1 маленькой переделке. Фрагмент, приведенный выше, заменим на такой (**): if z = 0 then repeat until 1 = 2 else writeln('зациклится') Эту программу (назовем ее U2) сохраним в другом файле. Что делает U2? Она тоже, как и U1, получает на вход число i, но отличается от U1 вот чем: если выяснилось, что исследуемая программа со стандартным номером i не зацикливается на файле данных со стандартным номером i, то сама U2 зацикливается, а в противном случае U2 выдает сообщение “зациклится” и после этого завершает работу. Программа U2 сама тоже записана в файле. Этот файл обязательно находится в последовательности (*) и имеет некоторый стандартный номер. Пусть k — этот номер. Здесь начинается самое интересное. Что произойдет, если на вход программе U2 в качестве числа i мы подадим число k? В этом случае, конечно, выполнение программы U2 может либо зациклиться, либо остановиться. Предположим, что оно остановится. Тогда, как только компьютер дойдет до выполнения фрагмента (**), переменная z должна получить нулевое значение. После этого, в соответствии с (**), произойдет зацикливание. Предположив, что выполнение остановится, мы выяснили, что выполнение зациклится! Это невозможно. Теперь предположим, что выполнение зациклится. Но тогда программа U2, как говорилось выше, должна выдать сообщение “зациклится” и после этого остановиться. Это тоже невозможно. Таким образом, программа должна зациклиться, если она остановится, и должна остановиться, если она зациклится. В чем тут дело? Конечно же в том, что мы предполагали возможность написания универсальной программы U, которая определяла бы любую программу на возможность зацикливания. Итак, такой программы U не существует в принципе, или, как говорят математики, проблема останова алгоритмически неразрешима. Неразрешимость проблемы останова впервые была доказана Аланом Тьюрингом в его работе, опубликованной в 1936 г. Конечно, тогда не было никаких компьютеров и тем более языков программирования, да и сам Тьюринг в той работе даже не пользовался термином “программа”. Но его изложение, по сути, мало чем отличалось от нашего. Мы использовали язык Pascal и говорили о привычных нам компьютерах, однако ясно, что эти подробности (о файлах, о конкретном языке программирования) были совсем не важны: существо наших рассуждений было чисто логическим. Другие алгоритмически неразрешимые задачиУпомянутая в начале статьи проблема проверки правильности любых математических утверждений также оказалась алгоритмически неразрешимой. Сформулируем ее формально в более общем виде. Пусть у нас есть посылка R и следствие S, записанные в виде слов (формул) в некотором алфавите, состоящем из букв, цифр, скобок, знаков математических и логических операций. Процесс вывода следствия S из посылки R может быть описан путем указания последовательности допустимых формальных преобразований слов (дедуктивной цепочки). Проблему распознавания выводимости можно сформулировать следующим образом: Существует ли для любых двух слов R и S дедуктивная цепочка, ведущая от R к S? Решение понимается в смысле существования алгоритма, дающего ответ на этот вопрос для любых слов R и S. В 1936 г. американский математик Черч доказал теорему о том, что проблема распознавания выводимости алгоритмически неразрешима. Тем самым выяснилась причина безуспешности всех прошлых попыток решения задачи, поставленной Лейбницем. Неразрешимой оказалась и так называемая “10-я проблема Гильберта”. В упрощенной формулировке она звучит так: требуется выработать алгоритм, позволяющий для любого алгебраического уравнения P(x1, x2, …, xn) = 0, где P — многочлен с целыми коэффициентами, выяснить, имеет ли оно целочисленное решение. В 1970 г. советский математик Ю.В. Матиясевич доказал невозможность построения алгоритма для решения этой задачи. Интересно, что если для конкретного уравнения известно, что решение в целых числах есть, то алгоритм отыскания этого решения существует. Какие методы используются для доказательства алгоритмической неразрешимости? Обычно неразрешимость новых задач доказывается методом сведения к этим задачам известных алгоритмически неразрешимых задач. Тем самым доказывается, что если бы была разрешима новая задача, то можно было бы решить и заведомо неразрешимую задачу. Применяя метод сведения, обычно ссылаются на искусственные задачи, которые не представляют самостоятельного интереса, но для которых легко непосредственно доказать их неразрешимость, например, описанную выше проблему самоприменимости. Методические рекомендацииДанная тема включена в стандарт профильного курса информатики в следующей формулировке: диагональное доказательство несуществования. Здесь имеется в виду канторовский диагональный процесс, который можно использовать для доказательства алгоритмической неразрешимости, в частности, проблемы останова. Именно поэтому в качестве основного материала статьи приведено такое доказательство этой проблемы, которое легко сводится к рассуждениям Кантора. Следует лишь описать канторовские массив-таблицу Т и массив-строку D. В проблеме останова T[i,j] — крестик, если программа, реализованная в файле со стандартным номером i, зацикливается на данных, расположенных в файле со стандартным номером j, иначе — нолик. Значения T[i,j] для любых заданных i и j могла бы вычислять, после небольших модификаций, программа U (если бы, конечно, она существовала). Значение D[i] — нолик, если программа, реализованная в файле со стандартным номером i, зацикливается на данных, расположенных в файле со стандартным номером i, иначе — крестик. Значения D[i] можно было бы вычислять, используя программу U1. Тогда D[i] не равно Т[i,i] для всех индексов i и D не совпадает ни с одной строкой таблицы Т. А если бы программа U1 существовала, то она имела бы свой номер и ей соответствовала бы одна из строк таблицы T. Подробнее о канторовском диагональном процессе и соответствующем доказательстве проблемы останова можно прочитать в уже упомянутой статье И.Долмачева “Алан Тьюринг”, которую также можно найти на сайте газеты “Информатика” (в архивных материалах № 5/2000). Два других доказательства алгоритмической неразрешимости данной проблемы можно прочитать в учебнике Е.В. Андреевой, Л.Л. Босовой, И.Н. Фалиной “Математические основы информатики” (М.: БИНОМ. Лаборатория Знаний, 2005) и в методическом пособии к этому учебнику (М.: БИНОМ. Лаборатория Знаний, 2006). Выбор доказательства остается на усмотрение учителя. Например, если в курс информатики включается рассмотрение машины Тьюринга, то и доказательство алгоритмической неразрешимости можно проводить с использованием этого формального аппарата. Тем не менее сама тема имеет очень важное, в том числе культурологическое, значение, и в профильной школе должна быть рассмотрена обязательно, а в основной — по крайней мере должен быть сформулирован сам факт существования алгоритмически неразрешимых задач. Ведь сам по себе этот факт является весьма неочевидным, о чем говорят и многовековые попытки решить те или иные проблемы (задача доказать их возможную алгоритмическую неразрешимость при этом изначально даже не ставилась). Ученики также воспринимают данный факт с недоверием, причем даже после доказательства неразрешимости, например, проблемы останова. Ведь их практический опыт подсказывает, что очень часто они сами могут эту проблему для конкретной программы решить, в том числе и доказать, что определенная программа на конкретных входных данных зациклится. Здесь очень важно провести грань между решением задачи для частного случая и построением универсального алгоритма. Действительно, проблему останова для конкретной программы или даже класса программ решить можно. Так, для программы, состоящей только из линейных конструкций, легко показать, что она всегда закончит свою работу. Приведенное же доказательство говорит о невозможности построения общего алгоритма, пригодного для любых программ и входных данных. Особо следует отметить, что не решает данную проблему и компьютерный запуск программы на конкретных входных данных (такой способ часто предлагают сами школьники). В самом деле, если программа закончила свою работу, то мы можем сказать, что она не зацикливается. Однако если окончания работы программы мы не дождались, то это не означает ничего: программа может как зациклиться, так и просто долго работать. 3. Алгоритмические конструкцииВиды алгоритмических конструкцийДля записи алгоритмов существуют разные способы (см. “Способы записи алгоритмов”): текстово-формульная запись, блок-схема, машина Тьюринга, машина Поста, программа на алгоритмическом языке и др. Каждый алгоритм записывается в системе команд исполнителя. Вне зависимости от выбранной формы записи элементарные шаги алгоритма объединяются в алгоритмические конструкции (структуры): последовательные, ветвящиеся, циклические, вспомогательные алгоритмы (см. “Подпрограммы”) и рекурсивные. В 1966 году Бом и Джакопини доказали, что для записи любого сколь угодно сложного алгоритма достаточно трех основных алгоритмических конструкций: последовательных, ветвящихся, циклических.
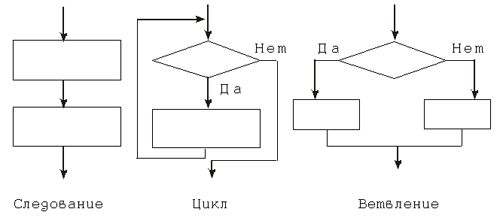
Алгоритм P (или его часть) реализован через последовательную алгоритмическую конструкцию (следование), если каждый шаг алгоритма выполняется один раз, причем после каждого i-го шага выполняется (i + 1)-й шаг, если i-й шаг — не конец алгоритма. Такой алгоритм или часть алгоритма еще называют линейным.
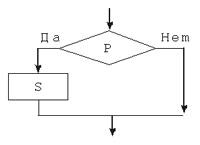
Пример 1. Линейным является алгоритм перевоза через реку Волка, Козы и Капусты, при условии, что в лодке можно перевозить только один из указанных объектов, а на берегу вместе не могут находиться Коза и Волк, а также Коза и Капуста: 1) перевези Козу; 2) вернись на исходный берег; 3) перевези Волка; 4) вернись на исходный берег с Козой; 5) перевези Капусту; 6) вернись на исходный берег; 7) перевези Козу. Алгоритм P реализован с использованием ветвящейся алгоритмической конструкции (ветвления), если на каком-либо шаге последовательное выполнение алгоритма прерывается, и выбор следующего шага определяется входными данными алгоритма. Ветвление задает выполнение либо одной, либо другой группы операторов в зависимости от выполнения какого-либо условия (в зависимости от истинности или ложности соответствующего логического выражения, см. “Логические выражения”). Затем исполнение алгоритма выходит на общее продолжение. Для конкретных входных данных ветвящаяся алгоритмическая конструкция сводится к последовательной алгоритмической конструкции. Ветвление бывает полным и неполным. В случае неполного ветвления при невыполнении условия никакие действия не выполняются.
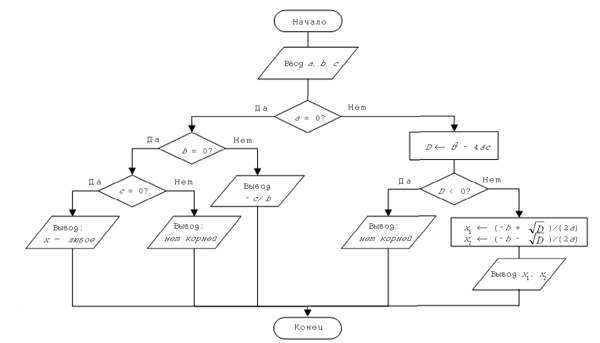
Пример 2. Запишем в словесной форме
алгоритм решения уравнения ax2 + bx + c
= 0, где a, b, c — произвольные
действительные числа, а x — искомая величина.
Если a
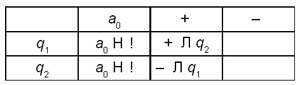
Алгоритм P реализован с использованием циклической алгоритмической конструкции, если некая, подряд идущая группа шагов алгоритма, выполняется несколько раз. Количество повторений либо фиксировано, либо зависит от входных данных алгоритма. Любая циклическая алгоритмическая конструкция содержит в себе элементы ветвящейся алгоритмической конструкции: после очередного выполнения группы шагов, входящих в цикл (которое называется шагом цикла, или итерацией), проверяется некоторое условие, формируемое в процессе вычислений. В зависимости от значения этого условия цикл либо завершается, либо начинается выполнение следующего шага цикла. В качестве примера алгоритма с циклической конструкцией можно рассмотреть алгоритм Евклида нахождения наибольшего общего делителя двух натуральных чисел (см. “Алгоритм”). Следование, ветвление и цикл называют базовыми конструкциями структурного программирования. Их особенностью является то, что любая из них имеет только один вход и один выход, поэтому они могут вкладываться друг в друга. Например, цикл может содержать следование из двух ветвлений, каждое из которых включает вложенные циклы. Запись конструкцийДля разных исполнителей основные алгоритмические конструкции могут реализовываться различным образом. Следование не имеет специальной формы записи, а выражается в том, что входящие в него шаги записываются последовательно, а управление после выполнения очередного шага этой конструкции переходит к следующему. В текстовой форме записи — это просто последовательная запись пунктов, соответствующих шагам алгоритма. В блок-схемах — это последовательная запись блоков действия, соединенных стрелкой, направленной от предыдущего блока к следующему. На процедурном языке программирования данная конструкция выражается просто последовательной записью инструкций (операторов языка программирования). Ветвление в текстовой форме записи обычно выглядит так: если выполнено такое-то условие, то сделать то-то (или перейти на такой-то пункт алгоритма), в противном случае сделать то-то (или перейти на такой-то пункт алгоритма). В блок-схемах для реализации конструкции ветвление предназначен специальный блок условия, имеющий форму ромба. Данный блок имеет один вход и два выхода, соответствующих истинному или ложному значению логического выражения, записанного в этом блоке. В языках программирования данная конструкция реализуется через условный оператор (см. “Операторы языка программирования”). В машине Тьюринга ветвление реализуется через анализ текущего состояния машины и текущего символа на ленте машины Тьюринга (в зависимости от символа и от состояния машины на ленту записывается определенный символ и совершается переход в определенное состояние). Циклическая конструкция в явном виде во многих формах записи алгоритмов, к сожалению, отсутствует. На практике она реализуется с помощью проверки условия и управляющей конструкции перехода. В текстовой форме записи переход осуществляется на тот же самый пункт или пункт с меньшим номером. В блок-схемах переход с помощью стрелок осуществляется на часть схемы, по которой выполнение алгоритма уже ранее проходило. В языках программирования циклическая конструкция реализуется через различные операторы цикла: “с предусловием”, “с постусловием”, “с параметром”. На самом деле для реализации любой циклической конструкции хватило бы и одного вида оператора, например, с “предусловием”, различные операторы циклов вводятся в тот или иной язык программирования только для удобства программистов. Пример 3. Рассмотрим следующую задачу. Пусть на вход алгоритму подается последовательность символов “+”. Требуется заменить каждый второй символ этой последовательности на “–”. Для машины Тьюринга эта задача может быть переформулирована так. На ленте машины Тьюринга содержится последовательность символов “+”. Напишите программу для машины Тьюринга, которая каждый второй символ “+” заменит на “–”. Автомат в состоянии q1 обозревает крайний левый символ в указанной последовательности. Решение
В состоянии q1 машина пропускает
знак “+”, а при достижении конца
последовательности — останавливается. В
состоянии q2 машина знак “+” заменяет
на знак “–”, при достижении конца
последовательности она останавливается. “–”
является символом алфавита этой машины, но он нам
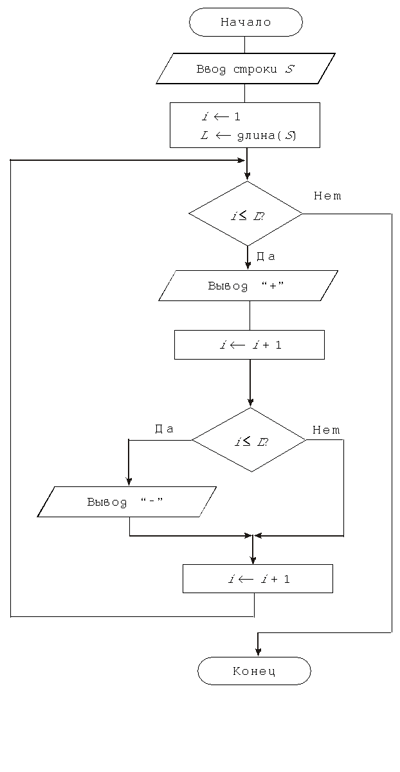
встретиться не может. Решение той же задачи с помощью блок-схемы можно записать так:
На языке программирования Pascal программа решения этой задачи может выглядеть так: var S: string; i: integer; begin readln(S); for i := 1 to length(S) do if i mod 2 = 0 then S[i] := '–'; writeln(S) end. Структурное программированиеЭдсгер В. Дийкстра, опираясь на теорему Бома и Джакопини, ввел понятие структурного программирования, которое часто называют “программирование без GOTO” (управляющая конструкция перехода не используется при написании программ).
В соответствии с данным способом разработки любая программа представляет собой структуру, построенную из трех типов базовых конструкций, рассмотренных выше. Еще один из принципов структурного программирования состоит в том, что программная единица (подпрограмма) должна иметь одну точку входа и одну точку выхода. Соблюдение принципов структурного программирования делает тексты программ, даже довольно больших, нормально “читаемыми”, что существенно облегчает понимание программ, — появилась возможность разработки код в промышленном режиме, когда код может без особых затруднений понять не только ее автор, но и другие программисты. Методические рекомендацииЗнакомство с основными алгоритмическими конструкциями начинается в пропедевтическом курсе информатики. К сожалению, запись алгоритмов с помощью блок-схем не приучает к структурному мышлению и выделению циклических конструкций в явном виде (исключение составляют специальные циклические блоки, которые часто не изучаются, как избыточные). Поэтому роль учителя состоит в том, чтобы на примерах показать, насколько необдуманные переходы запутывают алгоритм. Саму же разработку алгоритмов надо сразу проводить со школьниками по структурной схеме, используя технологию “сверху вниз” (см. “Подпрограммы”). В начальной школе, а также в 5–7-х классах при изучении алгоритмики отработке подлежит составление алгоритмов, содержащих циклическую алгоритмическую конструкцию, как наиболее сложную для понимания. При отработке конструкции ветвления очень полезно разобрать приведенный в материалах статьи алгоритм решения обобщенного квадратного уравнения (a может быть равно 0). Часто ученики не могут корректно сформулировать часть алгоритма, возникающую при a = 0. Кроме того, при написании соответствующей программы они часто используют сложные условия вида: if (a = 0) and (b = 0) and (c = 0) then … На самом же деле в данном случае алгоритм реализуется через конструкцию ветвления, условием которой служит проверка на равенство a нулю, в зависимости от истинности этого условия выполняется либо последовательная конструкция (вычисление дискриминанта, проверка его знака и связанное с ней вычисление корней), либо снова конструкция ветвление и т.д. В средней и старшей школе основное внимание необходимо уделять особенностям реализации базовых конструкций в различных языках программирования, т.е. синтаксису и семантике операторов выбора, цикла, присваивания (см. “Операторы языка программирования”). 4. Высказывания. Логические значенияПонятие высказыванияВысказывание — это повествовательное предложение, о котором можно (по крайней мере в пределах определенного контекста) говорить, что оно истинно или ложно (Х.Фрейденталь)2. Высказывания являются одним из основополагающих видов носителей информации3. Примерами высказываний на русском языке являются предложения: “Вчера было полнолуние”, “Москва — столица Российской Федерации”. Для определенного объекта, как, например, луна, город, страна, высказывания характеризуют определенные свойства или состояния, с помощью высказываний мы устанавливаем взаимосвязи между объектами. Высказывание будет истинным, если оно адекватно отображает эту связь, в противном случае оно ложно. Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание “Число 1 + 225 = 4 294 967 297 — простое”, принадлежащее Ферма (1601–1665), долгое время считалось истинным, пока в 1732 году Эйлер не доказал, что оно ложно. Изучением высказываний как математических объектов занимается алгебра логики. Однако обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания “Сумма углов треугольника равна 180о” устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным. Приведенное выше определение высказывания не является математически точным. Оно отсылает проблему определения высказывания к проблеме определения истинности или ложности данного языкового образования. Если рассматривать в качестве высказываний любые утвердительные предложения, то это быстро приводит к парадоксам и противоречиям. Например, предложению “Это предложение является ложным” невозможно приписать никакого значения истинности без того, чтобы не получить противоречие. Действительно, если принять, что предложение истинно, то это противоречит его собственному утверждению. Если же принять, что предложение ложно, то отсюда следует, что предложение на самом деле истинно. Как видно, этому предложению осмысленно нельзя приписать какое-либо значение истинности, следовательно, оно не является высказыванием. Причина этого парадокса лежит в структуре построения указанного предложения: оно ссылается на свое собственное значение. С помощью определенных ограничений на допустимые формы высказываний могут быть устранены такие ссылки на себя и, следовательно, устранены возникающие отсюда парадоксы. Высказывания могут выражаться с помощью математических, физических, химических и прочих знаков. Например, из двух чисел можно составить высказывания, соединив их знаками равенства или неравенства: “5 < 7” (истинное высказывание), “5 = 7” (ложное высказывание). Понятие высказывательной формыОднако не всякое повествовательное предложение является высказыванием. Например, в предложении “х < 12” не содержится никакого утверждения, следовательно, нельзя ставить вопрос о его истинности или ложности. Но это предложение становится высказыванием при замене переменной х каким-либо конкретным значением. Буква х, входящая в это предложение, играет роль переменной. Переменная — это языковое выражение, служащее для обозначения произвольного объекта из некоторого конкретного множества, называемого областью допустимых значений этой переменной. Если переменная употребляется таким образом, что вместо нее допускается подстановка любого значения из области допустимых значений, то эта переменная называется свободной. Так, переменная х в предложении “х < 12” является свободной. Переменные a, b, с и y в предложении ay2 + by + c = 0 также являются свободными. Однако встречается такое употребление переменных, например, в математике, которое не предполагает и не допускает возможность подстановки вместо переменных конкретных имен объектов (значений). Так, предложение “Не существует действительной переменной z, квадратный корень которой равен –1” содержит переменную z, однако подстановка конкретных значений вместо переменной z лишена какого-либо смысла. В случае, когда по смыслу выражения, содержащего переменную, подстановка вместо нее конкретных значений невозможна, эта переменная называется связанной. Повествовательное предложение, содержащее свободные переменные, называется высказывательной формой. Например, предложения типа “х < 12” есть высказывательная форма. Логические переменные и логические значенияВысказывание называется простым или элементарным, если никакая его часть сама не является высказыванием. Если высказывание является истинным, то говорят, что его истинностное значение есть И (истина), если высказывание является ложным, то его истинностное значение есть Л (ложь). Как уже было сказано ранее, обоснование истинности или ложности простых высказываний решается вне логики. Из элементарных высказываний можно получать новые, более сложные высказывания. Способ построения сложного высказывания из элементарных высказываний, при котором истинностное значение сложного высказывания полностью определяется истинностными значениями исходных высказываний, называется логической операцией (см. “Логические операции. Кванторы”). В русском языке сложные высказывания из элементарных высказываний строятся при помощи логических связок типа: и, или, а, но, либо, если … то, неверно, что... и т.д. Логической переменной называется переменная, значением которой может быть любое, наперед заданное высказывание. Логические переменные обозначаются латинскими буквами, быть может, снабженными индексами, как обычные алгебраические переменные: x, y, x1, y1, xk, yn и т.п. Очевидно, что логические переменные могут принимать только значения “истина” или “ложь”. Эти значения называют логическими. В алгебре логики, в языках программирования для обозначения значений логических переменных используют также 1 или true (истина), 0 или false (ложь). Методические рекомендацииКак уже было сказано в статье, высказывания являются одной из основных форм представления информации. Действительно, с помощью высказываний мы можем описывать свойства объектов (“Число 5 — нечетное”, “15 апреля 2007 года в Хабаровске был ураганный ветер”), взаимоотношения объектов (“Если в ромбе все углы прямые, то это — квадрат”, “Дробь является правильной только тогда, когда ее числитель меньше знаменателя”). При помощи высказываний мы записываем алгоритмы в текстовой форме, строим информационные системы и т.д. Каждое элементарное высказывание в определенной системе контекста несет значение истина или ложь. Одну из первых попыток постичь понятие высказывания предпринял древнегреческий ученый и философ, основоположник формальной логики Аристотель (384–322 до н.э.). Он писал: “Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности”. Для точного определения понятия высказывания и формальной работы с высказываниями в информатике строятся специальные формальные системы. В рамках таких систем мы можем представлять информацию в формальном виде, например, в виде логических формул, — так называемая внешняя форма представления информации, вычислять значение информации (в смысле описания свойств объекта, взаимоотношений объектов и т.д.) — так называемая собственно “абстрактная” информация. Манфред Брой (немецкий ученый, лауреат премии Лейбница в области информатики) дает следующее определение информации: “Информацией называют абстрактное содержание (“содержательное значение”, “семантика”) какого-либо высказывания, описания, указания, сообщения или известия. Внешнюю форму изображения информации называют представлением информации”. Выявление подходящих систем представления (“языков”) для определенных классов информации является одной из задач информатики. Понятие высказывания вводится в средней школе, как правило, в 8–9-м классе. Однако с этим понятием учащиеся начинают работать с младших классов. Авторы некоторых учебников называют высказывания суждениями. Однако дело не в терминологии. Важно, чтобы школьник научился понимать, является ли конкретное предложение высказыванием или нет, чтобы он умел обосновать свой ответ. Если в рамках изучаемой темы (например, “Человек и информация” или “Основы алгоритмизации и программирования”) школьникам приходится строить сложные высказывания и определять их истинность, то последовательность изложения материала может быть следующая: · понятие простого и сложного высказывания; · понятие истинности высказывания; · знакомство с основными логическими связками; · отработка навыков построения сложных высказываний, устанавливающих взаимосвязь между объектами; · отработка навыков построения высказываний, описывающих заданные объекты. 5. Игры и выигрышные стратегииОпределение игрыЧеловек с самого детства и всю жизнь играет в игры. И если некоторое представление о детских, логических и компьютерных играх имеют все, то далеко не все знают, что, например, выбор банка, в котором следует открыть счет, — это тоже игра (в математическом смысле слова). В математике существует специальный раздел — теория игр, в котором изучаются свойства игр в широком смысле. Определимся сразу, что мы будем рассматривать не все игры, а только их определенный класс. Нас будут интересовать игры с противоречивыми интересами сторон (антагонистические игры) и полной информацией об игре, и в первую очередь такая разновидность подобных игр, как игра двух лиц с нулевой суммой. Игра двух лиц (в дальнейшем будем называть их первый игрок и второй игрок, подразумевая игроков, которые ходят первым и вторым соответственно) с нулевой суммой означает, что выигрыш одного игрока является проигрышем другого (в ряде игр возможна ничья).
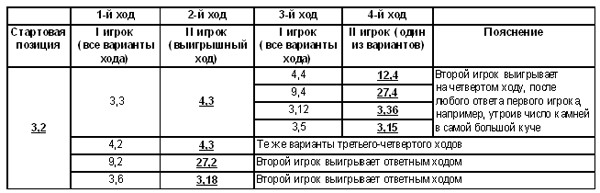
В рассматриваемых нами играх участвуют два игрока, которые ходят по очереди, причем оба они обладают полной информацией о текущей игровой ситуации (это определение исключает большинство карточных игр) и о возможных ходах очередного игрока. Игра считается оконченной, если достигнута позиция, являющаяся согласно правилам игры “терминальной” (конечной, заключительной), например, матовая позиция в шахматах. Правилами игры также устанавливается, каков исход игры в этой терминальной позиции. Чтобы задать конечную игру с полной информацией4, нужно: · указать конечное множество, элементы которого называются позициями игры; · указать начальную позицию игры; · указать множество заключительных позиций и задать результат игры в каждой из них; · для каждой из остальных позиций указать возможные ходы, т.е. позиции, которые могут случиться после хода первого или второго игрока соответственно (в некоторых играх возможные ходы не зависят от того, какой именно игрок ходит). При этом в игре не должно быть бесконечных партий (бесконечных последовательностей позиций, в которых игроки ходят по правилам, но так и не попадают в заключительную позицию). Если к тому же ни в каких аспектах игры (правилах, возможности или очередности ходов, определении момента завершения игры или результата) не участвует элемент случайности, такая игра будет еще и детерминированной. Примерами рассматриваемых нами игр являются большинство настольных игр: шахматы, шашки, го, крестики-нолики, реверси и многие другие. В математике большое распространение получили игры с камнями, в которых в распоряжении двух игроков имеются несколько кучек камней (одна или более). Игроки ходят по очереди. Также определено, сколько камней и из какого количества кучек может взять игрок за один ход. Если за один ход можно взять любое ненулевое число камней, но только из одной из кучек, то такая игра называется ним. Позициями в таких играх являются различные состояния кучек, которые можно получить из начального состояния (очевидно, что в каждой из кучек может оказаться не больше камней, чем было изначально). Пусть у нас было n кучек по k камней в каждой. Тогда общее число позиций равно (k + 1)n. Здесь учитывается, что в каждой из кучек в процессе игры камней может и не остаться. Поэтому в первой кучке может находиться от 0 до k камней, для каждого состояния первой кучки во второй также может находиться от 0 до k камней и т.д. Часть позиций, возможно, неотличимы друг от друга с точки зрения игры. Заключительной является единственная позиция, в которой ни в одной из кучек камней не осталось. Обычно по правилам она считается проигрышной (тот, кто не может сделать очередной ход, проигрывает), но можно считать ее и выигрышной, тогда такую игру называют “в поддавки”. Классификация позиций и стратегии игроковПусть в нашей игре не бывает “ничьих” и игроки ходят по очереди. Нетерминальная позиция называется выигрышной, если в ней существует какой-нибудь разрешенный ход, приводящий к выигрышу. С другой стороны, некоторая нетерминальная позиция является проигранной для игрока, если все разрешенные ходы из этой позиции ведут к позициям, в которых возможен выигрыш противника. Запишем это более формально. Нетерминальная позиция x называется выигрышной для игрока, которому предоставлен ход, если существует хотя бы один ход, переводящий игру в проигрышную позицию. Нетерминальная позиция x называется проигрышной, если все ходы из позиции x ведут в выигрышные позиции. Стратегией в конечной игре с полной информацией называется правило, указывающее, как следует игроку ходить в каждой из позиций, где ход за ним. Понятие стратегии не надо отождествлять с понятием хода. Стратегия определяет полный план действий игрока при всевозможных ситуациях, могущих возникнуть в игре. Стратегия называется выигрышной для игрока, если все партии, в которых он придерживается этой стратегии, заканчиваются выигрышем этого игрока. Покажем, что в рассматриваемом нами классе игр обязательно существует выигрышная стратегия для одного из игроков, а все позиции игры можно разделить на выигрышные и проигрышные. Конечную игру с полной информацией можно представить в виде ориентированного графа (см. “Структуры данных”), вершинами которого являются все допустимые позиции игры, а ребра указывают возможные ходы. Данный граф обязательно будет ациклическим (не будет содержать циклов), в противном случае окончание игры не гарантировано. Будем назначать значение для каждой вершины этого графа (выигрышная или проигрышная) по таким правилам: · значение вершин, соответствующих терминальным позициям, однозначно определено правилами игры; · все вершины, из которых хотя бы одно ребро графа ведет в вершину, помеченную как проигрышную, помечаем как выигрышные; · все вершины, из которых все ребра графа ведут в выигрышные позиции, помечаем как проигрышные. Эти правила применяем в любом порядке,
пока это возможно. Утверждается, что рано или
поздно всем позициям игры будут присвоены
определенные значения. В самом деле, если
какая-то вершина графа оказалась непомеченной,
то она не может быть заключительной. Более того,
какая-то из следующих за ней позиций тоже
осталась непомеченной (иначе мы смогли бы
пометить и эту), значит, и у нее какая-то из
следующих не имеет пометки и т.д. Так как все позиции оказались помеченными, то помечена и начальная позиция. Если она оказалась выигрышной, то при правильной игре первый игрок гарантированно выигрывает и его выигрышная стратегия состоит в том, чтобы на каждом ходу ставить противника в проигрышную позицию (наличие такого хода обеспечено правилом, по которому помечалась соответствующая вершина графа). Если же она помечена как проигрышная, то гарантированно выигрывает второй игрок при любом ходе первого игрока. Из доказанного утверждения следует, что результат многих логических игр, в том числе и шахмат, предсказуем. Почему же мы не только не знаем выигрышную стратегию для большинства популярных игр, но открытым остается и вопрос, кто имеет гарантированный выигрыш в каждой из них? Дело здесь в астрономическом числе возможных позиций. Например, в шахматах это число оценивают сверху как 10120. Оно находится за пределами возможностей компьютеров в обозримом будущем. Программирование игрГоворя даже об определенном классе игр, нельзя не упомянуть компьютерные программы, играющие в различные игры из данного класса. Как, например, компьютеры играют (и, как мы знаем, весьма успешно) в шахматы? Ведь полный анализ данной игры пока невозможен. Как и люди, компьютеры просчитывают варианты для текущей позиции — они смотрят, какие возможны ходы, какие ответы возможны на каждый из ходов и т.д. Просмотр приходится на каком-то уровне прерывать и грубо оценивать позицию как выигрышную или проигрышную в зависимости от материального перевеса и расположения фигур. К этому еще добавляется библиотека начал (дебютов), накопленная многовековым опытом шахматистов, а также сведения об окончаниях (эндшпилях), часть из которых, в свою очередь, удалось за последние годы просчитать на компьютере. Если же игра такова, что число позиций в ней, по меркам современных компьютеров, не велико (скажем, не превосходит 106), то игру можно полностью просчитать, начиная с терминальных позиций. Соответствующая программа будет существенно более эффективной, если значения уже просчитанных позиций будут запоминаться в памяти компьютера и не пересчитываться повторно. Для этого, помимо прочего, надо научиться все позиции нумеровать (в ряде игр это может быть весьма нетривиальной задачей). При этом часть позиций можно будет и не просчитывать вообще: если для какого-то хода игрока выясняется, что он ведет в проигрышную позицию, то другие варианты хода можно уже не рассматривать (текущая позиция выигрышная). К счастью, для ряда игр просчитывать большое число позиций для определения результата игры не требуется. В них удается выигрышную стратегию описать с помощью простой функции, аргументом которой является позиция, а значением — выигрышный ход для данной позиции или сообщение о том, что позиция является проигрышной. Рассмотрим пример такой игры5. На столе лежат N камней. Играющие по очереди могут взять от одного до четырех камней. Кто не может сделать ход (камней не осталось) — проигрывает. Если N делится на 5 без остатка, то второй игрок может гарантировать себе выигрыш, дополняя ход противника до 5 (если первый взял одну, то второй берет четыре и т.д.). Если N на 5 не делится, то выигрывает первый игрок: он должен сначала взять число камней, равное остатку от деления N на 5, а потом дополнять ход противника до 5. Здесь все позиции с числом камней кратным 5 являются проигрышными, остальные — выигрышными. Программирование выигрышной стратегии для такой игры не составит труда. Часто в играх используется и так называемая “симметричная стратегия”. Например, двое игроков кладут одинаковые круглые монеты на прямоугольный стол. Монеты могут свешиваться за край, но не должны падать и перекрываться. Кто не может положить монету — проигрывает. В этой игре первый игрок может выиграть, положив первым ходом свою монету в центр стола, а затем повторяя ходы второго игрока симметрично относительно центра. Очевидно, что если второй игрок нашел место для монеты, то есть и пустое симметричное ему место. В этой игре число позиций бесконечно (хотя сама игра конечна), но идея симметрии применяется и в ситуациях с конечным числом позиций. Методические рекомендацииТема выигрышные стратегии в играх появилась в профильном уровне стандарта среднего (полного) общего образования по информатике. Изучение темы “Игры и выигрышные стратегии” позволяет показать ученику научный подход к решению ряда бытовых задач, расширяет их кругозор с точки зрения практической применимости знаний математики и алгоритмов. Ранее подобные задачи встречались лишь на олимпиадах по информатике и программированию и опирались на знания, полученные учащимися математических классов в углубленном курсе математики. Начиная с 2005 г. задачи на поиск выигрышной стратегии встречаются и в материалах ЕГЭ по информатике. Приведем пример задачи из демоверсии ЕГЭ 2007 г. Задача. Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 3, а во второй — 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет один камень в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 16 камней. Кто выигрывает при безошибочной игре обоих игроков — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте. Решение. Выигрывает второй игрок. Для доказательства рассмотрим неполное дерево игры, оформленное в виде таблицы, где в каждой ячейке записаны пары чисел, разделенные запятой. Эти числа соответствуют количеству камней на каждом этапе игры, в первой и второй кучах соответственно. Приведенная на с. 36 таблица содержит все возможные варианты ходов первого игрока. Из нее видно, что при любом ходе первого игрока у второго имеется ход, приводящий к победе. В бескомпьютерном варианте предлагаемые задачи по информатике на данную тему таковы, что общее число позиций в игре позволяет провести практически полный ее анализ так, как было рассказано в материалах статьи. Программирование стратегий одного из игроков в различных логических играх может стать хорошей темой для кружковой и внеклассной работы учащихся (подготовка к конференциям, турнирам игровых программ, в которых программы играют между собой, и т.п.). 6. Исполнитель алгоритмовАлгоритмы и исполнителиПонятие алгоритма непосредственно связано с представлением об исполнителе алгоритма (см. статью “Алгоритмы”).
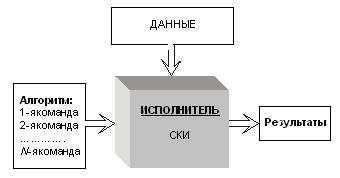
Взаимосвязь понятий отражена на рисунке:
Схема функционирования исполнителя алгоритмов Множество команд, которые может выполнять исполнитель, составляют систему команд исполнителя (СКИ). Алгоритм строится из команд СКИ. Объекты, над которыми исполнитель может совершать действия, составляют так называемую среду исполнителя. Данные и результаты, изображенные на рисунке, — это объекты, относящиеся к среде исполнителя. Основные свойства алгоритма (дискретность, понятность, определенность, конечность) обеспечивают возможность формальной работы исполнителя. Отсюда следует, что исполнителем алгоритмов может быть автоматическое устройство. Класс задач, на решение которых ориентирован исполнитель, определяется его системой команд. В методике обучения алгоритмизации принято выделять две категории исполнителей: исполнители, работающие “в обстановке”, и исполнители, работающие с величинами. Для первой категории средой исполнителя может быть лист (экран), на котором исполнитель формирует изображения (рисунки, чертежи и пр.); лабиринт, который исполнитель должен преодолеть; предметы, которые исполнитель должен расставить в определенном порядке, и т.п. Исполнители работы с величинами предназначены для обработки числовой или символьной информации. Исполнитель, в систему команд которого входят арифметические и логические операции, может решать вычислительные задачи. Входными данными и результатами для него являются числа. Универсальным исполнителем алгоритмов для работы с величинами является компьютер. Учебные исполнителиУчебные исполнители алгоритмов — это программные средства, предназначенные для обучения алгоритмизации. Исторически первым педагогическим
программным средством, предназначенным для
обучения детей алгоритмизации, был язык
программирования LOGO, разработанный в конце 1960-х
годов американским педагогом-психологом
С.Пейпертом. В состав LOGO входит исполнитель
Черепашка, назначение которого — изображение на
экране чертежей, рисунков, состоящих из
прямолинейных отрезков. Программы управления
Черепашкой составляются из команд: вперед(а),
назад(а), направо(в), налево(в), поднять
хвост, опустить хвост. Имеется в виду, что
Черепашка рисует хвостом, и если хвост опущен, то
при перемещении проводится линия, а когда хвост
поднят, то линия не рисуется. Кроме того, в языке
имеются все основные структурные команды. Применение исполнителей, работающих
“в обстановке”, получило широкое
распространение в отечественных учебниках
информатики как для начальной, так и для основной
школы. Например, в пропедевтическом курсе
“Роботландия” (авторы: Совокупность среды и СКИ исполнителя можно назвать архитектурой исполнителя. Основным дидактическим достоинством учебных исполнителей алгоритмов является наглядность архитектуры исполнителя. Успешность обучения алгоритмизации на учебных исполнителях алгоритмов объясняется тем, что ученикам понятен смысл решаемых задач и ясна архитектура исполнителя. Как известно, дидактический принцип наглядности является одним из важнейших в процессе любого обучения. Компьютер как исполнитель алгоритмовПонятие исполнителя используется и при обучении программированию для ЭВМ. Составление любой программы для компьютера начинается с построения алгоритма. Всякий алгоритм (программа) составляется для конкретного исполнителя, в рамках его системы команд. О каком же исполнителе идет речь в теме “Программирование для ЭВМ”? Ответ очевиден: исполнителем является компьютер. Точнее говоря, исполнителем является комплекс “компьютер + система программирования (СП)”. Программист составляет программу на том языке, на который ориентирована СП. Иногда в литературе по программированию такой комплекс называют “виртуальной ЭВМ”. Например, компьютер с работающей системой программирования на Бейсике называют “Бейсик-машина”; компьютер с работающей системой программирования на Паскале называют “Паскаль-машина” и т.п. Схематически это отражено на рисунке. Систему команд такого исполнителя называют входным языком. Входным языком исполнителя, представленного на рисунке, является язык программирования Паскаль.
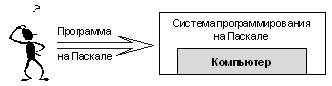
Взаимодействие программиста с компьютером Методические рекомендацииОбучение методам построения алгоритмов — один из наиболее отработанных разделов школьной информатики. Традиционно применяемым дидактическим средством в этом разделе являются учебные исполнители алгоритмов. Некоторые из таких исполнителей перечислены выше. Для целей обучения подходит любой исполнитель, который удовлетворяет следующим условиям: · это должен быть исполнитель, работающий “в обстановке”; · этот исполнитель должен имитировать процесс управления некоторым реальным объектом (черепахой, роботом и др.); · в системе команд исполнителя должны быть все структурные команды управления (ветвления, циклы); · исполнитель позволяет использовать вспомогательные алгоритмы (процедуры). Последние два пункта означают, что на данном исполнителе можно обучать структурной методике алгоритмизации. Всякое педагогическое средство должно соответствовать поставленной учебной цели. Главной целью раздела алгоритмизации является овладение учащимися структурной методикой построения алгоритмов. Как уже говорилось выше, успешность использования учебных исполнителей для обучения алгоритмизации связана с понятностью для учеников их архитектуры (среды и СКИ). Получив условие задачи, ученик “проектирует” решение этой задачи на архитектуру исполнителя и в результате получает алгоритм решения задачи данным исполнителем.
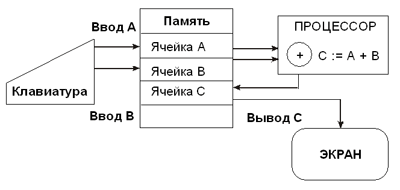
Аналогичный подход должен лежать в основе методики обучения программированию решения вычислительных задач. Исполнителем вычислительных алгоритмов (алгоритмов работы с величинами) является компьютер. Предлагается следующий подход к описанию архитектуры такого исполнителя. В состав исполнителя входят: память, процессор, устройство ввода, устройство вывода. Память используется для хранения данных и программы, процессор реализует вычисления и управляет работой всех устройств компьютера; устройства ввода (например, клавиатура) и вывода (например, монитор) обеспечивают взаимодействие между компьютером и человеком. Под всякую величину, используемую в алгоритме, выделяется ячейка памяти. Основные (неструктурные) команды
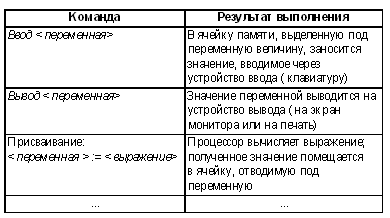
Замечание: на первых порах вместо полного описания команды: вывод <выражение> можно ограничиться частным вариантом: вывод <переменная>. Позже (для языков программирования) ее следует уточнить. Вот как нужно пояснять процесс выполнения алгоритма сложения двух чисел:
Описанный механизм выполнения алгоритма схематически представлен на рисунке.
Исполнение компьютером вычислительного алгоритма 7. Логические выраженияПонятие логического выражения или логической формулы вводится индуктивно. Логической формулой является 1) любая логическая переменная (переменная, принимающая одно из двух значений: истина или ложь, обозначаемых далее 1 и 0 соответственно), а также каждая из двух логических констант (постоянных) — 0 и 1, является формулой; 2) если A и B — формулы, то Формулой является, например, следующее
выражение (x & y) Формулы А и В, зависящие от одного и того же списка переменных x1, x2, x3, …, xn, называют равносильными, или эквивалентными, если на любом наборе значений переменных x1, x2, x3, …, xn они принимают одинаковые значения. Для обозначения равносильности формул используется знак равенства, например, А = В. Любую формулу можно преобразовать к
равносильной ей, в которой используются только
операции &, Для преобразования формул в равносильные важную роль играют следующие равенства, отражающие свойства логических операций, справедливые для любых переменных x, y, z. Эти свойства называют законами алгебры логики:
Любой из этих законов может быть легко доказан с помощью таблиц истинности, или путем логических рассуждений, или с помощью тождественных преобразований, использующих доказанные ранее законы. Приоритет выполнения логических операцийДля логических операций в одном логическом выражении установлен следующий порядок вычислений: · отрицание — первый, наивысший приоритет; · конъюнкция — второй приоритет; · дизъюнкция, разделительная дизъюнкция — третий приоритет; · импликация, эквивалентность — низший приоритет. Изменить порядок выполнения операций можно с помощью расстановки скобок. В алгебре логики дизъюнкция
(логическое сложение) играет роль, аналогичную
сложению в алгебре действительных чисел,
конъюнкция (логическое умножение) — умножению, а
отрицание (инверсия значения логической формулы)
— унарному минусу (инверсия знака обычной
формулы). Операция эквивалентность аналогична
операции отношения “=”, а операция импликация —
операции отношения “ Очевидно, что если имеется логическая формула, то, используя тождественные преобразования, можно изменить ее, построив сколь угодно сложную равносильную формулу. Одна из основных задач алгебры логики — нахождение канонических форм (т.е. формул, построенных по определенному правилу, канону), а также формул, имеющих наиболее простой вид. Если логическая формула выражена через дизъюнкцию, конъюнкцию и отрицание, то такая форма представления называется нормальной. Среди нормальных форм выделяют такие, в которых функции записываются единственным образом. Их называют совершенными. Особую роль в алгебре логики играет класс совершенных дизъюнктивных нормальных форм. В их основе лежат понятия элементарной дизъюнкции и элементарной конъюнкции. Формулу называют элементарной конъюнкцией, если она является конъюнкцией одной или нескольких переменных, взятых с отрицанием или без отрицания. Например, формулы x2, x2, x1 & x3, x1 & x3 & x1 & x3 являются элементарными конъюнкциями. Формула называется дизъюнктивной нормальной
формой (ДНФ), если она является дизъюнкцией
элементарных конъюнкций. ДНФ записываются в виде
A1 Формула А от k переменных называется совершенной дизъюнктивной нормальной формой (СДНФ), если 1) А является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция k переменных x1, x2, …, xk, причем на i-м месте этой конъюнкции стоит либо переменная xi, либо ее отрицание; 2) все элементарные конъюнкции в такой ДНФ попарно различны. Совершенная дизъюнктивная нормальная форма представляет собой формулу, построенную по строго определенным правилам с точностью до порядка следования элементарных конъюнкций (дизъюнктивных членов) в ней. Она является примером однозначного представления булевой функции в виде формульной (алгебраической) записи. Логической функцией называется функция, аргументы которой и сама функция принимают значения 0 или 1. Логические функции могут быть заданы таблично (таблицей истинности) или в виде соответствующих формул. Тем самым каждая формула может рассматриваться как способ задания логической функции. При этом одна и та же функция может задаваться различными формулами. Возникает вопрос: всякую ли логическую функцию можно представить в одном из канонических совершенных видов? Да, любую булеву функцию, не равную тождественно лжи, можно представить в виде СДНФ. Сформулируем это утверждение в виде следующей теоремы. Теорема. Пусть — f (x1, x2, …, xn)булева функция от n переменных, не равная тождественно нулю. Тогда существует совершенная дизъюнктивная нормальная форма, выражающая функцию f, которую можно построить по следующему алгоритму: 1. В таблице истинности отмечаем наборы переменных, на которых значение функции f равно единице. 2. Записываем для каждого отмеченного набора конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае — ее отрицание. 3. Все полученные конъюнкции связываем операциями дизъюнкции. Доказательство. Каждая элементарная конъюнкция, вошедшая в СДНФ, принимает значение 1 только на единственном наборе. Отсюда следует, что если функция на каком-то наборе равна 1, то и вся СДНФ равна 1 в силу того, что по построению соответствующая элементарная конъюнкция, вошедшая в СДНФ, равна 1. А если функция равна 0, то и СДНФ равна 0, т.к. на этом наборе равны 0 все вошедшие в СДНФ элементарные конъюнкции. Таким образом, СДНФ равносильна исходной функции. Следствие. Любую логическую функцию можно представить формулой, в которой используются только логические операции дизъюнкции, конъюнкции и отрицания. Доказательство. Для всех функций, отличных от 0, это можно сделать с помощью СДНФ, а ноль можно выразить, например, как x &`x. Методические рекомендацииУмения строить логические выражения (логические формулы), вычислять их значение, выполнять над ними тождественные преобразования требуются при изучении разных тем информатики: при построении алгоритмов, в программировании, при решении логических задач, конструировании запроса при работе с БД, при работе с электронными таблицами и т.п. Для формирования этих умений важно обращать внимание на следующие моменты. 1) Любое логическое выражение (логическая формула) реализует логическую функцию на конечном наборе различных значений переменных, в него входящих. Часто (при построении запросов или условия ветвления) по словесному описанию логического выражения (логического условия) требуется построить его аналитическое выражение. Словесное выражение является высказыванием. Для правильного построения логического выражения вначале в сложном высказывании необходимо выделить элементарные высказывания, а затем, используя семантику языковых связок, построить формулу. Такое умение можно формировать уже в базовом курсе информатики. 2) Во многих языках программирования
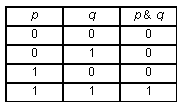
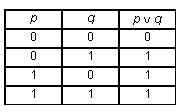
используется только несколько логических
операций, как правило, операция логического
сложения, логического умножения и отрицания, а
также операция разделительной дизъюнкции.
Поэтому, если полученная формула содержит не
только операции &, 3) Для построения СДНФ учащиеся должны уметь без ошибок строить таблицу истинности для конкретной логической формулы. А для этого надо требовать, чтобы учащиеся строго соблюдали порядок перечисления набора значений переменных: если каждый набор значений переменных рассматривать как двоичное число, то все числа должны быть записаны в порядке возрастания. Например, для формулы от трех переменных перечисление набора значений в таблице истинности должно быть выполнено в следующем порядке: 4) Перед изложением формулировки
теоремы о СДНФ надо пояснить, для чего
используются нормальные формы (поиск
аналитического вида булевой функции, заданной
таблицей истинности; минимизация представления
булевой функции с использованием только трех
логических операций &,
5) Если вы задаете своим ученикам задания на построение отрицания к сложному высказыванию (а проще всего это делать через построение отрицания к соответствующему логическому выражению), то им следует пояснить, почему в этом случае квантор общности заменяется на квантор существования и наоборот (см. “Логические операции. Кванторы”). Очевидно, что высказывание, содержащее квантор общности (например, “Все мужчины старше 70 лет имеют длинную седую бороду”), можно заменить на следующее: “И Иванов А.П., и Кравцов И.Г., и Петухов С.П., и … старше 70 лет и имеют длинную седую бороду”. Это высказывание можно записать следующей формулой: И & К & П & …, где буквой И обозначено высказывание “Иванов А.П. (который старше 70 лет) носит длинную седую бороду”, буквой К обозначено высказывание “Кравцов И.Г. носит длинную седую бороду” и т.д. При построении отрицания к первоначальному сложному высказыванию, содержащему квантор общности, воспользуемся законом де Моргана. Тогда получим:
Этой формуле соответствует высказывание “Или Иванов А.П. не имеет длинной седой бороды, или Кравцов И.Г. не имеет длинной седой бороды, или Петухов С.П. ... или … не имеет длинной седой бороды”, другими словами, “Существует мужчина старше 70 лет, который не имеет длинной седой бороды”. 8. Логические операции. КванторыЛогические операцииВ любом национальном языке употребляемые в обычной речи связки “и”, “или”, “если …, то …”, “тогда и только тогда, когда …” и т.п. позволяют из уже заданных высказываний строить новые сложные высказывания. Истинность или ложность получаемых таким образом высказываний зависит от истинности и ложности исходных высказываний и соответствующей трактовки связок как операций над высказываниями. Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает сложное высказывание при всех возможных значениях простых высказываний. Логической операцией называется способ построения сложного высказывания из элементарных высказываний, при котором истинностное значение сложного высказывания полностью определяется истинностными значениями исходных высказываний (см. статью “Высказывания. Логические значения”). В алгебре логики логические операции и соответствующие им логические связки имеют специальные названия и обозначаются следующим образом:
Конъюнкция — логическая операция, ставящая в соответствие каждым двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны7. Логическая операция конъюнкция определяется следующей таблицей истинности:
Рассмотрим два высказывания: p = “Завтра будет мороз” и q = “Завтра будет идти снег”. Очевидно, новое высказывание p & q = “Завтра будет мороз, и завтра будет идти снег” истинно только в том случае, когда одновременно истинны высказывания p и q, а именно, что завтра будет и мороз и снег. Высказывание p & q будет ложно во всех остальных случаях: будет идти снег, но будет оттепель (т.е. не будет мороза); мороз будет, а снег не будет идти; не будет мороза, и снег не будет идти. Дизъюнкция — логическая операция, ставящая в соответствие каждым двум элементарным высказываниям новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны, и истинным, когда хотя бы одно из двух образующих его высказываний истинно8. Логическая операция дизъюнкция определяется следующей таблицей истинности:
Рассмотрим два высказывания: p = “Колумб
был в Индии” и q = “Колумб был в Египте”.
Очевидно, что новое высказывание p Союз “или” может применяться в речи и в другом, “исключающем” смысле. Тогда он соответствует другому высказыванию — разделительной, или строгой, дизъюнкции. Строгая, или разделительная, дизъюнкция — логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным только тогда, когда только одно из высказываний является истинным. Логическая операция разделительная дизъюнкция определяется следующей таблицей истинности:
Рассмотрим два высказывания: p = “Кошка
охотится за мышами” и q = “Кошка спит на
диване”. Очевидно, что новое высказывание p В логике связкам “либо” и “или” придается разное значение, однако в русском языке связку “или” иногда употребляют вместо связки “либо”. В этих случаях однозначность определения используемой логической операции связана с анализом содержания высказывания. Например, анализ высказывания “Петя сидит на трибуне А либо на трибуне Б” заменить на “Петя сидит на трибуне А или Б”, то анализ последнего высказывания однозначно укажет на логическую операцию разделительная дизъюнкция, т.к. человек не может находиться в двух разных местах одновременно. Импликация — логическая операция, ставящая в соответствие каждым двум элементарным высказываниям новое высказывание, являющееся ложным тогда и только тогда, когда условие (посылка) — истинно, а следствие (заключение) — ложно. Подавляющее число зависимостей между событиями можно описать с помощью импликации. Например, высказыванием “Если на каникулах мы поедем в Петербург, то посетим Исаакиевский собор” мы утверждаем, что в случае приезда на каникулах в Петербург Исаакиевский собор мы посетим обязательно. Логическая операция импликация задается следующей таблицей истинности:
Импликация будет ложной только тогда, когда посылка истинна, а заключение ложно, и она заведомо будет истинна, если ее условие p ложно. Причем для математика это вполне естественно. В самом деле, исходя из ложной посылки, можно путем верных рассуждений получить как истинное, так и ложное утверждение. Допустим, 1 = 2, тогда и 2 = 1. Складывая эти равенства, мы получим 3 = 3, т.е. из ложной посылки путем тождественных преобразований мы получили истинное высказывание. Импликация, образованная из высказываний А и В, может быть записана при помощи следующих предложений: “Если А, то В”, “Из А следует В”, “А влечет В”, “Для того чтобы А, необходимо, чтобы В”, “Для того чтобы В, достаточно, чтобы А”. Эквивалентность — логическая операция, ставящая в соответствие двум элементарным высказываниям новое, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны. Логическая операция эквивалентность задается следующей таблицей истинности:
Рассмотрим возможные значения сложного высказывания, являющегося эквивалентностью: “Учитель поставит ученику 5 в четверти тогда и только тогда, когда ученик получит 5 на зачете”. 1) Ученик получил 5 на зачете и 5 в четверти, т.е. учитель выполнил свое обещание, следовательно, высказывание является истинным. 2) Ученик не получил на зачете 5, и учитель не поставил ему 5 в четверти, т.е. учитель свое обещание сдержал, высказывание является истинным. 3) Ученик не получил на зачете 5, но учитель поставил ему 5 в четверти, т.е. учитель свое обещание не сдержал, высказывание является ложным. 4) Ученик получил на зачете 5, но учитель не поставил ему 5 в четверти, т.е. учитель свое обещание не сдержал, высказывание является ложным. Отметим, что в математических теоремах эквивалентность выражается связкой “необходимо и достаточно”. Рассмотренные выше операции были двухместными (бинарными), т.е. выполнялись над двумя операндами (высказываниями). В алгебре логики определена и широко применяется и одноместная (унарная) операция отрицание. Отрицание — логическая операция, которая каждому элементарному высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному. Логическая операция отрицание задается следующей таблицей истинности:
В русском языке для построения отрицания используется связка “неверно, что …”. Хотя связка “неверно, что …” и не связывает двух каких-либо высказываний в одно, она трактуется логиками как логическая операция, поскольку, поставленная перед произвольным высказыванием, образует из него новое. Отрицанием высказывания “У меня дома есть компьютер” будет высказывание “Неверно, что у меня дома есть компьютер” или, что в русском языке то же самое, “У меня дома нет компьютера”. Отрицанием высказывания “Я не знаю китайского языка” будет высказывание “Неверно, что я не знаю китайского языка” или, что в русском языке одно и то же, “Я знаю китайский язык”. КванторыВ математической логике наряду с логическими операциями используются и кванторы. Квантор (от лат. quantum — сколько) — логическая операция, дающая количественную характеристику области предметов, к которой относится выражение, получаемое в результате ее применения. В обычном языке носителями таких характеристик служат слова типа все, каждый, некоторый, любой, всякий, бесконечно много, существует, имеется, единственный, несколько, конечное число, а также все количественные числительные. В формализованных языках, составной частью которых является исчисление предикатов, для выражения всех подобных характеристик оказывается достаточным кванторов двух видов: квантора общности и квантора существования.
Кванторы позволяют из конкретной высказывательной формы (см. “Высказывания. Логические значения”) получить высказывательную форму с меньшим числом параметров, в частности, из одноместной высказывательной формы получить высказывание9. Квантор общности позволяет из
данной высказывательной формы с единственной
свободной переменной x получить высказывание
с помощью связки “Для всех x …”. Результат
применения квантора общности к высказывательной
форме A(x) обозначают
Квантор существования позволяет из
данной высказывательной формы с единственной
свободной переменной x получить высказывание
с помощью связки “Существует такой x, что …”.
Результат применения квантора общности к
высказывательной форме A(x) обозначают Кванторы играют для формализованных языков математической логики ту же роль, которую играют для естественного языка так называемые “количественные” (“кванторные”) слова, — определяют область применимости данного высказывания (или высказывательной формы). При построении отрицания к высказыванию, содержащему квантор, действует следующее правило: частица “не” добавляется к сказуемому, квантор общности заменяется на квантор единственности и наоборот. Рассмотрим пример. Отрицанием высказывания “Все юноши 11-х классов — отличники” является высказывание “Неверно, что все юноши 11-х классов — отличники” или “Некоторые юноши 11-х классов — не отличники”. В информатике кванторы применяются в логических языках программирования (см. “Языки программирования”) и языках запросов к базам данных. Методические рекомендацииУмение строить сложные высказывания требуется при работе с базами данных, при конструировании запроса поиска в Интернете, при построении алгоритмов и написании программ на любом алгоритмическом языке. Более того, это умение можно отнести к общешкольным умениям, т.к. оно связано с построением сложных умозаключений (рассуждений, получений выводов). В основе этого умения лежат знание основных логических операций и умение определять истинность сложных высказываний. С логическими операциями дизъюнкция, конъюнкция и отрицание школьники знакомятся в основной школе. Там же вводится и понятие таблицы истинности. Скорее всего знакомство с данными понятиями возникает в языках программирования, но использовать их можно и в электронных таблицах — там логические операции реализованы через соответствующие функции OR, AND, NOT. Более сложные логические операции
могут быть рассмотрены в старшей школе. Задачи,
использующие импликацию, встречаются в каждом из
опубликованных вариантов ЕГЭ по информатике.
Например: для какого числа X истинно
высказывание ((X > 3) При изучении операции импликации следует обратить внимание учащихся на тот факт, что большинство математических теорем являются импликациями. Однако те импликации, в которых посылки (условия) и заключения (следствиями) являются предложениями без взаимной (по существу) связи, не могут играть в науке более или менее важной роли. Они являются совершенно бесплодными предложениями, т.к. не ведут к выводам более глубокого содержания. Действительно, в математике ни одна теорема не является импликацией, в которой условие и заключение не были бы связаны по содержанию. Помимо связки “если, … то …”, в математических теоремах импликациями являются формулировки только необходимого или только достаточного условия. Задания на построение достаточных и необходимых условий для школьников оказываются непростыми. При формировании этого умения необходимо особо отметить три момента: а) используемая в математических утверждениях форма “необходимо и достаточно” соответствует связке “тогда и только тогда” (эквивалентность); б) связка “для того чтобы …(A),
необходимо, чтобы …(B)” реализуется прямой
импликацией A в) достаточное условие реализуется обратной импликацией B ® A и может на русском языке выражаться, например, так: “для того чтобы... (А), достаточно, чтобы... (В)”. В старшей школе (10–11-е классы) у учащихся полезно сформировать умение строить отрицание к высказыванию на русском языке. Это умение необходимо, например, для доказательства теорем методом “от противного”. Строить отрицание даже к простым высказываниям не всегда просто. Например, к высказыванию На стоянке стоят красные “Жигули” следующие предложения отрицаниями являться не будут: 1) На стоянке стоят не красные “Жигули”; 2) На стоянке стоит белый “Мерседес”; 3) Красные “Жигули” стоят не на стоянке. Отрицанием к этому высказыванию будет “На стоянке не стоят красные “Жигули”. Объяснить школьникам это можно так: отрицание к предложению должно полностью исключать истинность исходного высказывания. Если же на стоянке стоит белый “Мерседес”, то ничто не мешает красным “Жигулям” стоять тоже. Об алгоритме построения отрицания к сложному высказыванию можно прочитать в книге Е.Андреевой, Л.Босовой, И.Фалиной “Математические основы информатики”. Изучение кванторов до настоящего времени не было традиционным для школьного курса информатики. Однако теперь они входят в стандарт профильной школы. Проще всего продемонстрировать роль кванторов при построении все тех же отрицаний к высказываниям на русском языке, причем как к математическим, так и произвольным. Правило замены квантора общности на квантор существования и наоборот легко обосновать с помощью законов де Моргана (см. “Логические выражения”). 9. Объектно-ориентированное программированиеПо мере совершенствования вычислительной техники компьютеры стали использоваться для решения все более и более сложных задач. Оказалось, что для решения сложных задач важна не только повышенная вычислительная мощность компьютеров, но и эффективность написания сложных программ. Объектно-ориентированное программирование (ООП) появилось именно как эффективный способ преодоления трудностей, возникающих при создании сложных программ. Наиболее значимой частью ООП является особый подход к решению сложных задач программирования, называемый объектно-ориентированным анализом, а объектно-ориентированные языки программирования — просто удобные инструменты для реализации этого подхода. ИсторияОснователи ООП — выдающиеся норвежские ученые Кристен Нигаард (Cristen Nygaard) и Оле-Йохан Даль (Ole-Johan Dahl). Работая над моделированием судовождения, Нигаард понял, что существующие программные средства малоэффективны в создании столь сложных программ, и тогда Нигаард начал разрабатывать концепции нового программирования, позволяющего преодолеть барьеры сложности, и которое впоследствии было названо объектно-ориентированным (сам термин был придуман Аланом Кеем, автором языка Java). Вместе с Оле-Йоханом Далем Нигаард разработал основные положения ООП и практические механизмы их реализации, которые затем были воплощены в первом ООЯ Симула (Simula). Заслуги этих ученых были по достоинству оценены мировым научным сообществом, и в 2001 году Нигаард и Даль стали лауреатами премии имени Алана Тьюринга — своеобразного аналога Нобелевской премии в области computer science.
Язык Симула пользовался известностью в академических кругах, однако по ряду причин не завоевал популярности среди разработчиков коммерческого ПО. Тем не менее основные идеи и возможности ООП были очень привлекательны для программистов. Впоследствии были созданы другие ООЯ: SmallTalk (1980), C++ (1985), Eiffel (1986), Object Pascal (1986) и Delphi (1995), Oberon-2 (1991), Java (1991), Visual Basic (1991) и многие другие. Некоторые из этих языков стали промышленными стандартами в программировании. Особенности ООПОсновная идея ООП заключается в том, что следует создавать программные структуры, поведение и взаимодействие которых имитирует поведение и взаимодействие объектов реального мира (т.е. в программе как бы создаются виртуальные аналоги реальных сущностей). Объектно-ориентированные языки программирования должны предоставлять средства для удобного и быстрого воплощения этого подхода. В обыденной жизни люди используют (пусть даже неосознанно) различные приемы “экономии мышления”, позволяющие осмысливать и выражать сложные явления в простых понятиях. Типичными приемами “экономии мышления” являются: · абстрагирование (отбрасывание несущественных деталей); · обобщение (выделение общих существенных признаков у разных явлений или предметов); · классификация (осознание связи между явлениями и степени их схожести). Эти простые приемы помогают человеку справиться со сложностью рассматриваемых явлений. И объектно-ориентированные языки программирования также должны предоставлять подобные средства для “борьбы со сложностью” программ. Для реализации объектно-ориентированного подхода в языки программирования вводятся новые понятия: · объекты — особые программные структуры, объединяющие данные и алгоритмы их обработки; · инкапсуляция — сокрытие подробностей функционирования объектов; · наследование — “сокращенный” способ создания новых классов; · полиморфизм — возможность применения нескольких реализаций одной функции. Объекты и классыОбъекты — особые программные единицы, состоящие из данных и алгоритмов для обработки именно этих данных. Данные, входящие в состав объекта, называются полями (атрибутами, свойствами, членами). Алгоритмы, входящие в состав объекта, называются методами (сервисами, операциями, функциями-членами). К сожалению, единой устоявшейся терминологии в ООП нет, и в разных языках используются различные термины для обозначения одних и тех же понятий. Классы — это объектные типы данных. Подобно тому, как целые числа принадлежат какому-нибудь целочисленному типу (например, integer или byte), объекты также принадлежат какому-либо объектному типу — классу. Все объекты одного класса имеют одинаковый набор полей и одинаковый набор методов. В некоторых языках (C++, Java) объекты называются экземплярами класса (instances). Полезность использования классов и объектов заключается в том, что проверка логического (смыслового) соответствия между данными и функциями для обработки данных становится тривиальной задачей и может быть в основном переложена на компилятор (компьютер) — теперь он сам может определить неверное использование данных. ИнкапсуляцияИнкапсуляция (дословно — “сокрытие”) — контролируемое сокрытие информации о внутренней структуре класса. В классе могут быть поля и методы, используемые объектами исключительно для обеспечения своей работы (например, буфер в динамической памяти, файл с рабочими данными, методы для работы с этим файлом и т.п.). Изменять такие поля или вызывать методы извне объекта опасно — это может нарушить его рабочее состояние. Для обеспечения безопасности объектов подобные поля и методы можно скрыть — запретить обращение к ним извне. С позиций “борьбы со сложностью” инкапсуляция позволяет переложить часть контроля за правильностью работы с объектами на компилятор (компьютер). Различные ООЯ предлагают разные возможности по инкапсуляции полей и методов (от полного отсутствия и до автоматического сокрытия всех полей). В промышленных ООЯ, таких, как C++, Java, Delphi, Eiffel и т.д., предусмотрены три уровня инкапсуляции полей и методов: · public — на обращение к публичным полям и методам объектов нет никаких ограничений; · protected — прямое обращение к защищенным полям и методам возможно только из методов данного класса и методов дочерних классов; · private — прямое обращение к приватным полям и методам возможно исключительно из методов данного класса. НаследованиеНаследование — создание новых классов путем дописывания только отличий от уже существующих классов, опуская описания совпадающих элементов. При наследовании новый класс называется классом-потомком (производным, дочерним, подклассом), а исходный класс называется классом-предком (базовым, родительским, суперклассом). Наследование сокращает размер программы за счет исключения повторных описаний. Все поля и методы, объявленные в классе-предке, автоматически переносятся в класс-потомок, и их принято называть унаследованными (inherited). При необходимости любой родительский метод можно переопределить — т.е. назначить выполнение другого алгоритма в случае вызова одноименного метода класса-потомка. Некоторые ООЯ поддерживают множественное наследование, при котором производный класс наследует все свойства и методы одновременно от нескольких классов. К сожалению, множественное наследование таит в себе немало логических конфликтных ситуаций, а его поддержка усложняет язык программирования, и особенно — компилятор. По этой причине во многих ООЯ множественное наследование просто запрещено, но его можно сымитировать. Совокупность всех классов-предков и классов-потомков называется иерархией классов. Наследование классов — центральное понятие ООП, на нем прямо или косвенно базируются все остальные понятия и механизмы. Абсолютному большинству механизмов ООП, чтобы проявить свои преимущества, требуется построение иерархий классов. ПолиморфизмПолиморфизм (дословно — “многообразие форм”) — возможность использовать одно имя для нескольких методов (или функций), имеющих сходное назначение. Другая интерпретация — один метод (функция) может иметь несколько вариантов реализации; такой метод (функция) называется полиморфным. Подобно другим механизмам ООП, полиморфизм является средством упрощения разработки сложных программ. Фактически полиморфизм отделяет понятие, что надо сделать, от того, как это надо делать. Если провести аналогию с реальной жизнью, то полиморфизм соответствует обобщенным действиям. Например, глагол “музицировать” означает “играть на музыкальном инструменте”. Но на разных музыкальных инструментах играют по-разному. Термин один, а вариантов действия — много. Значит, “музицировать” — полиморфное действие. В ООП действию “музицировать” соответствовал бы полиморфный метод, имеющий свои реализации для каждого класса музыкальных инструментов. В ООП есть два вида полиморфных методов — перегруженные и виртуальные. Перегруженные методы предназначены для выполнения одинаковых по смыслу операций с данными разных типов. Они имеют одинаковые имена, но разные списки аргументов и/или тип возвращаемого значения. Виртуальные методы предназначены для выполнения одинаковых по смыслу операций в объектах родственных, но не совпадающих классов. Виртуальные методы имеют одинаковые имена и прототипы. Их главная особенность — они всегда точно соответствуют реальному классу объекта. Типичный пример перегруженных функций — функция SQR в Паскале. Она вычисляет квадрат числа, причем для целых аргументов результат будет также целым, а для вещественных — вещественным. Достоинства виртуальных методов проявляются только при использовании иерархии классов. Типичная схема использования виртуальных методов такова: · В классе-предке иерархии объявляется полиморфный метод, который описывает некое полезное действие. При этом либо он использует виртуальный метод, либо сам является виртуальным. · В классах-потомках соответствующий виртуальный метод переопределяется — для каждого класса-потомка это полезное действие выполняется по-своему. · При вызове для объекта, принадлежащего классу-потомку, полиморфного метода на деле используется виртуальный метод класса-потомка (а не класса-предка). Яркий пример подобного использования виртуальных методов — система графического оконного интерфейса Delphi или Visual Basic: каждый видимый элемент графического интерфейса — кнопка, ползунок, окно и т.п. — должен быть потомком класса TControl. В классе TControl вводятся общие полиморфные методы отрисовки элементов графического интерфейса, а любой его потомок может нарисовать себя на экране своим собственным способом. Методические рекомендацииОбъектно-ориентированное программирование явно не упоминается в Стандарте 2004 года, хотя в Обязательном минимуме содержания образования по информатике для учащихся профильных заведений (Уровень Б) такая тема присутствовала: Объектно-ориентированное программирование: объект, свойства объекта, операции над объектом. Там же упоминалась и объектно-ориентированная технология программирования. Тем не менее ООП не просто вошло в практику преподавания информатики (программирования) многих школ, но и присутствует на страницах школьных учебников (Угринович Н.Д. Информатика и информационные технологии. Учебник для 10–11-х классов, 2005. М.: БИНОМ. Лаборатория Знаний). Кроме того, в пропедевтическом курсе информатики для начальной школы (рабочие тетради авторского коллектива под руководством А.Горячева. 1–4-е классы) также вводятся понятия объекта и его свойств. Технология (парадигма) ООП требует не столько освоения современной техники программирования, сколько умения разрабатывать объектную модель решаемой задачи. Для этого требуется хорошо знать базовые принципы ООП и программирования вообще, однако знание какого-либо ООЯ не является обязательным — об этом неоднократно писали основоположники и теоретики ООП. Так, Гради Буч в своей книге “Объектно-ориентированное проектирование и анализ” высказывает следующую максиму: “Писать программы в объектно-ориентированном стиле можно в любом (не объектно-ориентированном) языке программирования”. Для построения алгоритма по технологии ООП требуется сформировать список объектов, с которыми работает алгоритм, продумать свойства каждого объекта и реализовать алгоритм как взаимодействие описанных объектов. Как уже было сказано в статье, такой подход упрощает решение сложных задач, но в рамках школы (с учетом ограниченного числа часов) трудно придумать содержательные учебные задачи, которые бы не надуманно требовали использования технологии ООП в полной мере. Фактически же ООП в школе рассматривается лишь как неотъемлемая часть визуального и компонентного программирования в современных профессиональных системах программирования, а в качестве объектов используются готовые объектные библиотеки различного уровня — это и библиотеки для построения графического интерфейса Windows-приложений, и многоцелевые универсальные библиотеки типов данных (например, STL в С++). Для примитивного использования этих библиотек достаточно знать и уметь применять несколько простейших правил синтаксиса языка программирования. Однако такие “знания” никоим образом не приближают учащихся ни к профессиональному овладению языком программирования, ни даже к пониманию ООП. Но, видимо, ничего страшного в этом нет. Школьная информатика и в профильной школе не ставит своей целью подготовку профессиональных программистов. Преподавание ООП — это специальная тема, даже на соответствующих специальностях вузов ее часто не изучают в достаточном объеме. Не отрицая полностью предложение
некоторых преподавателей информатики поставить
объектно-ориентированный подход во главу угла
изучения программирования, в том числе в школе,
отметим, что ООП невозможно без таких базовых
понятий, как программа, исполнитель, переменная,
условие, цикл и т.д. Концепция ООП также включает
в себя классическое процедурное
программирование (см. “Подпрограммы”), как
механика Эйнштейна — механику Ньютона:
достаточно представить себе процедурную
программу как единственный объект с опущенным
для простоты именем. Поэтому в первую очередь
задача курса программирования в школе — научить
базовым вещам. И лишь при возможности работы с
современными визуальными средами
программирования (Delphi, Visual Basic, Visual C++ 1 При доказательстве алгоритмической неразрешимости этой проблемы использованы материалы статьи Ивана Долмачева “Алан Тьюринг”, “Информатика” № 5/2000. 2 Фрейденталь Х. Язык логики. М.: Наука, 1969. 3 Брой М. Информатика. Основополагающее введение: часть I. М.: Диалог–МИФИ, 1996. 4 См. книгу А.Шеня “Игры и стратегии с точки зрения математики”. М.: изд-во МЦНМО, 2007. 5 Игра приведена, в частности, в книге А.Шеня “Игры и стратегии с точки зрения математики”. 6 От латинских слов idem — тот же самый и potens — сильный; дословно — равносильный. 7 Это определение легко распространяется на случай n высказываний (n > 2, n — натуральное число). 8 Это определение, как и предыдущее, распространяется на случай n высказываний (n > 2, n — натуральное число). 9 Успенский В.А., Верещагин Н.К., Плиско В.Е. Вводный курс математической логики. М.: Физматлит, 2002. |