Курсы повышения квалификации

Математические основы информатики

А.Г. Гейн

Учебный план

Лекция 6. Логические модели в информатике (продолжение)

§ 20. Реляционные модели

Для многих систем искусственного интеллекта важной составной частью является информация о тех объектах, процессах и явлениях, с которыми предстоит иметь дело пользователю данной системы искусственного интеллекта. Каждый объект при этом описывается значениями некоторого набора параметров. Нередко такое описание удобно представлять в виде таблицы. Вот общий вид такой таблицы (см. рис. 17).

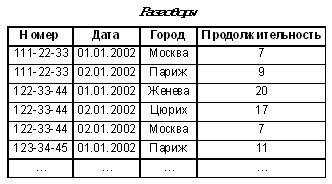
Рис. 17. Фактографическая модель. записанная в форме таблицы

Конечно, таких таблиц для данного набора объектов может быть несколько — в каждой из них фигурирует свой набор параметров. Более того, по мере накопления знаний об изучаемых объектах могут составляться новые таблицы — совсем необязательно новую информацию записывать в уже имеющуюся таблицу, увеличивая в ней набор столбцов. Совокупность таблиц, в которых для рассматриваемой совокупности объектов приведены значения параметров, описывающих эти объекты, называется реляционной моделью данной системы объектов.

Идея реляционной модели была предложена американским ученым Е.Ф. Коддом в начале 1970-х гг. Само слово “реляционная” происходит от англ. relation — отношение, связь. Иными словами, суть реляционного подхода заключается в том, что информация об объектах представляется в виде отношений, т.е. связанных между собой характеристик изучаемых объектов.

А сейчас обсудим, как с помощью такой модели можно получать нужную информацию. Приведенный ниже пример хотя и несколько далек от науки, но ярко показывает полезность таких моделей в разных областях человеческой деятельности.

Представим себе деятельность междугородней телефонной компании, например, в Санкт-Петербурге. Она предоставляет своим абонентам связь с другими городами. Информацию о предоставленных услугах связи удобно представлять таблицей (см. табл. 5.10).

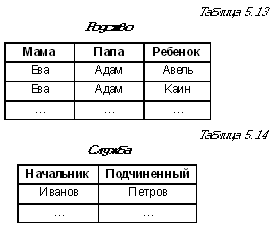
Каждый новый звонок добавляет строку в эту таблицу.

Но телефонная компания хранит, разумеется, и информацию о владельцах телефонов. Такая таблица может быть устроена, например, как табл. 5.11 (адреса и фамилии взяты нами, конечно, условно).

Пусть нас интересует, с какими городами и когда разговаривал Петров. Чтобы вычислить ответ, нужно проделать следующее:

— по заданному значению параметра Владелец в таблице Телефоны разыскиваем значение параметра Номер;

— по найденному значению параметра Номер в таблице Разговоры разыскиваем значения параметров Дата и Город;

— результат представляем новой таблицей (см. табл. 5.12).

Таким образом, чтобы получить нужную информацию, между таблицами необходимо установить связь, указав, какие параметры для них являются общими. В рассмотренном примере таким является параметр Номер.

Впрочем, в самой идее реляционности как раз нет ничего удивительного. Описывая окружающий мир, мы всегда не просто перечисляем его объекты, а обязательно называем отношения, которыми эти объекты связаны друг с другом. Рассмотрите для примера несколько фраз:

Дрозд — это птица;

Петр — отец Павла;

Васе нравится Аня;

Прямые a, b и c пересекаются в одной точке;

Маша взяла у Алеши книгу “Сказки 1001 ночи”.

В каждой из этих фраз фиксируется то или иное отношение между объектами. Первая фраза дает пример отношения принадлежности: дрозд принадлежит множеству птиц. Вторая и третья устанавливают отношения быть отцом между Петром и Павлом и нравится между Васей и Аней. Четвертая фраза указывает на отношение между тремя объектами. Наконец, пятая фраза описывает отношение между Машей, Алешей и конкретной книгой.

Разумеется, в одном и том же отношении могут находиться самые разнообразные объекты. Например, в отношении быть отцом находятся, конечно, не только Петр и Павел, но и многие другие пары людей. В отношении кто-то у кого-то что-то взял находятся тоже не только Маша, Алеша и “Сказки 1001 ночи”. Поэтому если сосредоточить внимание на самом отношении, то оказывается удобным считать, что отношение — это некое выражение с переменными:

Объект x — это отец объекту y;

Объект x взял у объекта y объект z;

и т.д.

Осталось сделать еще один шаг: унифицировать запись отношений. Это можно сделать, например, так:

быть_отцом(x, y);

взять(x, y, z);

и т.д.

То, что стоит перед скобками, — имя отношения, в скобках перечислены аргументы отношения, количество аргументов отношения называют его арностью. Так что первое из записанных в стандартной форме отношений бинарное (по-русски двухместное), второе тринарное (по-русски трехместное). Часто отношение между объектами, обозначенными, скажем, буквами a, b, c, d и т.д., схематично записывают так: R(a,b,c,d,...), где через R обозначено имя рассматриваемого отношения (первая буква от англ. relation — отношение). Впрочем, если отношение связывает только два объекта — a и b, то нередко пишут aRb. Например, мы пишем a < b для чисел, a || b — для прямых, a О A — для элемента a из множества A и т.п. Мы тоже будем так писать для уже устоявшихся обозначений отношений (равенства, неравенства, параллельности, принадлежности и т.п.).

В предложенном варианте записи отношения часть информации может оказаться утерянной. Скажем, из записи быть_отцом(x, y) уже не видно: то ли x — отец для y, то ли наоборот. Выход простой: для каждого аргумента указать, что он означает; можно сказать, что мы каждому аргументу присваиваем имя, фактически указывающее, из какого множества будут браться объекты для данного аргумента. Например:

быть_отцом(отец: x, ребенок: y);

взять(кто_взял: x, у_кого_взял: y, что_взял: z).

Имя аргумента нередко называют атрибутом данного отношения.

Ясно, что вместо аргументов нельзя подставлять любые объекты из тех множеств, которые обозначены атрибутами. Скажем, нельзя в отношении быть_отцом вместо x подставлять имя любого мужчины, а вместо y — имя любого ребенка. Как же тогда определять, каковы те наборы значений аргументов, для которых имеет место данное отношение? Иногда это настоящая детективная история, когда, например, следователь пытается выяснить, кто же без спросу взял у хозяина его бриллианты.

Вообще говоря, отношения могут задаваться по-разному. Нередко бывает так, что для каждого аргумента множество его значений конечно. В этом случае отношение можно задать списком всех тех наборов значений аргументов, которые находятся в данном отношении. А сам такой список, как было сказано выше, удобно представлять в виде таблицы, где каждая строка — это набор значений аргументов, находящихся в данном отношении, а каждый столбец — это перечень значений соответствующего атрибута. Сами атрибуты выступают при этом в роли заголовков столбцов.

Вот примеры отношений и представление их таблицами.

Эти отношения — “человеческие”. Но отношения могут быть между объектами любой природы. Ведь каждая таблица может рассматриваться как некое отношение. Железнодорожное расписание задает отношения между маршрутами, станциями и т.п. Таблица умножения задает отношение между числами.

Наличие отношения между характеристиками разных объектов или даже одного и того же объекта свидетельствует о зависимости этих характеристик друг от друга. Наиболее жестко характеристики оказываются связанными, если по значению одной из них можно определить значения остальных, находящихся в данном отношении. Такие отношения мы будем рассматривать в § 21. Но следует понимать, что даже если нет такой жесткой зависимости между параметрами, все равно отношение, не совпадающее со всевозможными наборами значений параметров, указывает на наличие некоторой связи между ними. Именно поэтому отношения стали важным инструментом построения и исследования самых разнообразных информационных моделей — ведь одним из компонентов информационной модели как раз является описание связей между ее параметрами.

Вопросы и ответы

1. Какую роль играет понятие отношения в информационном моделировании?

2. Как можно задавать отношения?

3. Из курса математики вы знаете, что графиком функции y = f(x) называется множество точек координатной плоскости, имеющих координаты (x, f(x)). Можно ли поэтому рассматривать график функции как способ задания некоторого отношения?

4. Пусть множество М состоит из чисел 1, 2, 3, 4, 5 и 6. На этом множестве заданы следующие отношения:

а) R1(х, у): число х делится на число у;

б) R2(х, у): числа х и у таковы, что | х – у | < 3;

в) R3(х, у): число х + у принадлежит множеству М.

Запишите каждое из этих отношений в виде таблицы.

5. Даны отношения нагрузка_учителей(фамилия:, класс:, предмет:) и расписание(класс:, предмет:, день_недели:, номер_урока:). Выберите 6–7 классов вашей школы и составьте для них таблицы, соответствующие указанным отношениям.

§ 21. Фуекциональные отношения

Понятие функциональной зависимости — одно из величайших изобретений человеческой мысли. И хотя слово “функция” у большинства людей ассоциируется с математикой, на самом деле с функциями человек имеет дело повсеместно. Но прежде, чем привести примеры, подтверждающие это высказывание, напомним, что функцией называется сопоставление каждому элементу одного множества ровно одного элемента из другого множества. Отметим, что это “другое множество” совсем не обязано отличаться от исходного.

В математике обычно рассматриваются числовые функции, т.е. оба множества — это множества чисел. На самом деле это совсем не обязательно. Вот примеры функций:

1) каждому человеку сопоставляется его фамилия (функция из множества людей в некоторое множество слов);

2) каждому человеку сопоставляется его рост (функция из множества людей в некоторое множество положительных чисел);

3) каждому городу России сопоставляется его почтовый индекс (функция из множества городов России в множество шестизначных натуральных чисел);

4) каждой точке на поверхности Земли сопоставляются ее географические координаты (функция из множества точек поверхности в некоторое множество пар, каждая компонента которой — положительное число с указанием северного или южного, восточного или западного полушарий);

5) каждому набору отпечатков пяти пальцев правой руки, имеющихся в картотеке МВД, сопоставляется человек с такими отпечатками.

Пусть нам дана некоторая функция f, сопоставляющая каждому элементу x из одного множества элемент y другого множества. Поскольку y по x определяется однозначно, то обычно пишут y = f(x). Определим отношение R, объявив пару (x, y) находящейся в отношении R в том и только том случае, если y = f(x). Впрочем, можно было определить отношение и другим образом: пара
(y, x) находится в отношении R*, если y = f(x).

Тем самым, каждая функция может быть описана как некоторое отношение, и даже не одно. Обратное, однако, неверно — ведь не у каждого отношения можно так выбрать атрибуты, чтобы значения одного из них однозначно определяли значения другого. Рассмотрим, к примеру, отношение “x является родным братом для y”. Конечно, если в семье только два брата, то для каждого x значение y определено однозначно. Однако есть семьи с большим числом братьев.

Говоря о представлении функции в виде отношения, мы имели в виду лишь бинарные отношения. Однако для функции значения аргумента, как и значения функции, вовсе не обязаны состоять из значений одного атрибута. Скажем, для функции, сопоставляющей набору отпечатков пяти пальцев имя, отчество и фамилию их владельца, аргумент содержит пять атрибутов, а значение функции — три. Записывая эту функцию как отношение, мы получим отношение с восемью атрибутами, разделенными на две группы: первая группа задает аргумент функции, вторая — ее значение.

Будем называть отношение функциональным, если его атрибуты можно разбить на две группы так, чтобы значения одной группы атрибутов однозначно определяли значения второй группы. Иными словами, первая группа атрибутов может рассматриваться как аргумент некоторой функции, а вторая группа определяет значение этой функции. Вовсе не обязательно при этом, чтобы атрибуты одной группы были соседними в записи отношения. Если отношение функционально, то набор атрибутов, относящихся к аргументу функции, задаваемой этим отношением, будем называть ключевым.

Рассмотрим для примера отношение, заданное уже рассматривавшейся таблицей Телефоны (см. табл. 5.11). Ясно, что атрибут Адрес не может быть ключевым, поскольку в одном доме оказалось несколько телефонов. Если среди владельцев имеются однофамильцы, то атрибут Владелец также не может быть ключевым. А вот Номер телефона — это ключевой атрибут. Впрочем, скорее всего ключевым будет и набор из двух атрибутов — Владелец-Адрес — слишком мала вероятность проживания в одном доме однофамильцев или владельца двух телефонных номеров сразу.

Для отношения, представленного таблицей, легко сформулировать критерий того, что данный набор атрибутов является ключевым. А именно, набор атрибутов ключевой, если в таблице нет двух строк с одинаковым набором значений этих атрибутов.

Вопросы и задания

1. Какое отношение называют функциональным? Приведите примеры функциональных отношений.

2. В § 20 в качестве примера рассматривалось отношение быть_отцом(отец: x, ребенок: y). Является ли это отношение функциональным? Если да, то какой атрибут служит аргументом, а какой — значением функции?

3. Рассмотрим отношение музыкальное_произведение (название: x, автор: y, характер произведения: z). Вот примеры значений аргументов, для которых отношение имеет место:

музыкальное_произведение(название: Пиковая дама, автор: П.И. Чайковский, характер произведения: опера);

музыкальное_произведение (название: Лебединое озеро, автор: П.И. Чайковский, характер произведения: балет);

музыкальное_произведение (название: Кармен, автор: Бизе, характер произведения: опера);

музыкальное_произведение(название: симфония
№ 8, автор: Л. ван Бетховен, характер произведения: симфония).

Является ли это отношение функциональным? Если да, то какой набор атрибутов можно рассматривать как ключевой?

4. Рассмотрим на множестве натуральных чисел отношение сумма(слагаемое1: x, слагаемое2: y, результат: z). Это отношение имеет место для чисел x, y и z в том и только том случае, когда z = x + y. Является ли это отношение функциональным? Если да, то какой набор атрибутов можно рассматривать как ключевой?

§ 22. Логические функции  и логические выражения

Логической функцией, или, по-другому, предикатом, на множестве M называют такую функцию от нескольких аргументов, которая при любом наборе значений этих аргументов из множества M принимает только одно из двух значений. Обычно одно из этих значений называют Истина, другое — Ложь. В языках программирования часто используются английские слова того же смысла True и False (реже Да и Нет или 1 и 0). Нередко предикат называют еще высказывательной формой, поскольку после подстановки вместо переменных элементов множества получается некое утверждение об этом наборе элементов, которое является либо истинным, либо ложным. Например, предикат “сумма x и y равна z” от трех аргументов x, y и z, рассматриваемый на множестве натуральных чисел, принимает значение Истина при x = 3, y = 4, z = 7 и значение Ложь при x = 2, y = 2, z = 5. По аналогии с общим обозначением в математике функции как f(x₁, x₂, …, x_n) в качестве общего обозначения предиката мы будем использовать запись Р(x₁, x₂, …, x_n). Впрочем, вместо Р может использоваться любая буква латинского алфавита.

В приведенном примере переменные x, y и z свободны в том смысле, что могут принимать любые значения из множества натуральных чисел. Поэтому данная логическая функция имеет три аргумента. Но не всегда число аргументов логической функции совпадает с числом фигурирующих в ее описании переменных. Рассмотрим, к примеру, такой предикат: “существует x, для которого сумма x и y равна z”. Хотя в описании фигурируют три переменных — х, y и z, — подставлять числа можно только вместо двух из них — y и z. Так что здесь только два аргумента: y и z. В табл. 5.15 приведены значения данной логической функции для некоторых наборов значений аргументов y и z (и этот предикат мы рассматриваем на множестве натуральных чисел).

Переменная x в такой функции называется связанной. При этом говорят, что переменная x связана квантором существования. Для него есть специальное обозначение: . Происхождение этого знака простое: в английском слове Exist — “существовать” взята первая буква и симметрично отражена относительно вертикальной оси. С помощью этого символа рассматриваемый нами предикат записывается так: x (x + y = z).

Впрочем, переменная может быть связанной и по-другому. Рассмотрим, для примера, опять на множестве натуральных чисел предикат “для любого y выполнено неравенство x + y > z”. Здесь связанной переменной является y. Вот значения этого предиката для нескольких наборов значений аргументов x и z.

В этом случае говорят, что переменная связана квантором всеобщности. Его обозначают символом “”. Его происхождение аналогично: от слова All — “все” взята первая буква и симметрично отражена относительно горизонтальной оси. С помощью этого квантора данный предикат запишется так:y (x + y > z).

В предикате могут оказаться связанными не одна, а несколько переменных. Например, можно рассматривать предикат y x (x + y = z). Или другой предикат: xy (x + y = z). Каждый из них является логической функцией от одного аргумента z, но это разные функции. Например, на множестве целых чисел первая из этих функций при любом значении аргумента z принимает значение Истина, в то время как вторая функция на том же множестве при любом значении аргумента z принимает значение Ложь. Так что порядок, в котором употреблены кванторы, имеет принципиальное значение.

Отметим, что если в предикате все переменные оказались связанными, то такой предикат является высказыванием. Например, предикат z y x (x + y = z) — это высказывание, утверждающее, что для любых чисел z и y существует их разность (она обозначена переменной x). Это высказывание истинно на множестве целых чисел, но ложно на множестве натуральных чисел. Поэтому, обсуждая свойства того или иного предиката, надо всегда указывать множество, на котором он рассматривается.

Над логическими функциями можно выполнять все те же логические операции, которые рассматривались нами для высказываний в § 16. Ведь для того, чтобы вычислить значение такой “составной” функции, достаточно знать логические значения функций, из которых она составлена. Например, логическая функция принимает значение Истина тогда и только тогда, когда логическая функция Р(x1, x2, …, xn) принимает значение Ложь.

При словесном описании логической функции построение отрицания к какому-либо утверждению можно выполнить добавлением словосочетания “Неверно, что…”, после чего следует исходное утверждение. Например, отрицание высказывания “Я пошел в кино” можно выразить так: “Неверно, что я пошел в кино”. Правда, таким образом свою мысль выражают крайне редко. Обычно говорят: “Я не пошел в кино”. Но заметьте, что ни одна из фраз “Не я пошел кино” и “Я пошел не в кино” не является отрицанием исходного высказывания.

А теперь рассмотрим, как строится отрицание высказывания, полученного связыванием переменой при помощи квантора. Вот пример высказывания: “Все ученики нашего класса имеют дома компьютер”. Конечно, его отрицанием является высказывание “Неверно, что все ученики нашего класса имеют дома компьютер”. Но каждому ясно, что это высказывание равносильно такому: “Существует ученик нашего класса, у которого дома нет компьютера”. Как видите, при построении отрицания квантор всеобщности преобразуется в квантор существования. Более точно, если через Р(х) обозначить предикат “ученик х имеет дома компьютер”, то исходное высказывание запишется так:х (Р(х)). А его отрицание запишется как x (P(x)). Аналогично можно объяснить, почему при построении отрицания квантор существования заменяется квантором всеобщности. Итак, для логических функций, имеющих вид Q1x1 Q2x2 … Qkxk (Р(x1, x2, …, xk, y1, y2, …, yn)), где Q1, Q2, …, Qk — символы или , x1, x2, … , xk — связанные переменные, y1, y2, …, yn — свободные переменные предиката Р, справедливо следующее правило построения отрицания: получается логическая функция, записанная в таком же виде, где каждый квантор всеобщности заменяется квантором существования и наоборот, а предикат Р заменяется его отрицанием.

Вопросы и задания

1. Какую функцию называют логической? Приведите примеры логических функций.

2. а) Для предиката “существует x, для которого сумма x и y равна z”, рассматриваемого на множестве натуральных чисел, назовите еще одну пару значений аргументов, для которых этот предикат истинен, и одну пару, для которой он ложен.

б) Для того же предиката, рассматриваемого на множестве слов русского языка (сложение здесь понимается как операция конкатенации), определите значение этого предиката, если y = ель, z = газель; y = гель, z = газель; y = газель, z = газель.

3. Для каждого из предикатов, приведенных в пунктах а) – в), укажите, сколько аргументов он имеет, и назовите, какие его переменные свободны, а какие связаны.

а) “Существует только один металл x, который в ряду активности располагается между элементами y и z”;

б) “Нет такого животного x, которое в ряду эволюции располагалось бы между животными y и z”;

в) “Для каждого химического элемента x существует химический элемент y, с которым x образует соединение”.

4. Рассмотрите предикаты, заданные на множестве натуральных чисел:

а) “х — нечетное число и для любого нечетного числа у выполнено неравенство х Ј у”,

б) “х — простое число и для любого простого числа у выполнено неравенство х Ј у”.

Для каждого из этих предикатов укажите все те значения аргумента х, для которого данный предикат истинен.

5. Рассмотрим предикат Р(х, у): “фигура х вписана в фигуру у”.

а) Пусть х пробегает множество всех треугольников, расположенных на некоторой плоскости, а у — множество всех окружностей на той же плоскости. Для высказыванийх у (Р(х, у)), х у (Р(х, у)), x y (Р(х, у)), х у (Р(х, у)) запишите каждое из них предложением русского языка. Определите, какие из них истинны, а какие ложны.

б) Выполните то же задание, что и в пункте а), если х пробегает множество всех окружностей, расположенных на некоторой плоскости, а у — множество всех треугольников той же плоскости.

6. Рассмотрим предикат Р(х, у): “фигура х вписана в фигуру у”.

а) Пусть х пробегает множество всех выпуклых четырехугольников, а у — множество всех окружностей. Укажите, для каких из четырех вариантов кванторных приставок х у, х у,x y, х у после связывания ими переменных в предикате Р(х, у) получается истинное высказывание.

б) Выполните то же задание, что и в пункте а), если х пробегает множество всех окружностей, а у — множество всех выпуклых четырехугольников.

7. В объяснительном тексте параграфа было показано, что логические функции х у (Р(х, у, z)) и у х (Р(х, у, z)), вообще говоря, различны.

а) Различны ли функции х у (Р(х, у, z)) и у х (Р(х, у, z)), где Р(х, у, z) — произвольный предикат от трех переменных? А функции х у (Р(х, у, z)) и у х (Р(х, у, z))?

б) Известно, что высказывание у х (Р(х, у)) истинно. Можно ли утверждать, что высказывание х у (Р(х, у)) тоже истинно?

8. На множестве натуральных чисел задан предикат U(x, y, z) — число z равно произведению чисел х и у. Используя этот предикат, запишите подходящей формулой каждое из следующих утверждений:

а) число х — делитель числа у;

б) числа х и у равны;

в) число х равно 1;

г) число х четно;

д) число х равно 2;

е) числа х и у взаимно просты (т.е. их наибольший общий делитель равен 1);

ж) число х простое;

з) число х является степенью простого числа.

9. а) На множестве действительных чисел задан предикат х (х2у – х(у – 3) + 1 >0). Укажите все значения переменной у, для которых этот предикат истинен.

б) Выполните то же задание, что и а), если предикат задан на множестве положительных чисел.

§ 23. Логика СУБД Access

Логические функции, рассматривавшиеся нами в качестве примеров в предыдущем параграфе, были довольно простыми и легко записывались на естественном языке. Но компьютер, как вы знаете, понимает только формальный язык. И любой формальный исполнитель, каким, в частности, является СУБД Access, тоже понимает только формальный язык. Вот об этом языке и пойдет у нас речь. Основу его составляют логические функции, о которых мы рассказывали в предыдущем параграфе.

А теперь вспомните ваш опыт обращения с обычными числовыми функциями. Изобретение буквенных обозначений переменных и языка формул для записи связей между ними стало революционным шагом. Вот и для логических функций естественно ввести некоторый язык формул, позволяющий относительно просто и достаточно стандартно записывать их. Строятся эти формулы, как и формулы в алгебре, из некоторых “кирпичиков”, соединенных знаками операций. Для алгебраических выражений “кирпичиками” выступают числа и переменные, в качестве операций выступают арифметические операции — сложение, умножение, вычитание и деление, — а также некоторые стандартные функции (показательная логарифмическая, тригонометрические и т.п.).

Что же выступает в роли “кирпичиков” логического выражения? Это некоторые стандартные предикаты, определяющие, истинно или ложно утверждение о том, что при заданных значениях переменных они находятся в заданном отношении.
В качестве таких отношений обычно фигурируют отношения сравнения = (равно), <> (не равно), < (меньше), > (больше) и т.п. Более точно можно сказать так: атомарным называется отношение вида А В, где А и В — однотипные выражения от переменных, а — один из символов отношения сравнения. Однотипность выражений означает, что после вычисления их значений для любого допустимого набора переменных мы получаем значения одного типа, например, числового, или символьного, или еще какого-либо.

Теперь можно формально определить логические выражения. Мы будем обозначать их большими латинскими буквами.

1. Всякое атомарное отношение есть логическое выражение.

2. Истина и Ложь — логические выражения.

3. Если А — логическое выражение, то выражение, то (А) — тоже логическое выражение.

4. Если А и В — логические выражения, то выражения А и В, А или В и не В тоже являются логическими.

Вот примеры логических выражений:

не (х = “СЛОН”),

(х = 2 + 2) и (у > 2*(х + 3)),

Правила 1–4 определяют формальную грамматику языка логических выражений. Заметим, что в определении логического выражения мы использовали не все логические операции, но это не сказывается на возможностях данного языка, поскольку, как вы знаете, операции следования, равносильности, исключающего или выражаются через указанные три операции. Но дело тут не в экономии используемых операций, а в том, что СУБД Access воспринимает, как мы чуть позже убедимся, язык логических выражений с операциями отрицания, дизъюнкции и конъюнкции.

Впрочем, с логическими выражениями вы наверняка уже встречались, изучая языки программирования. Собственно говоря, логические выражения и нужны именно для того, чтобы компьютеру на понятном для него языке сформулировать, с какой логической функцией ему надлежит иметь дело, чтобы помочь пользователю решить задачу.

Пусть теперь на множестве M нам дано некоторое отношение с атрибутами x₁, x₂, …, x_n. Рассмотрим логическую функцию от тех же переменных (не обязательно всех). Возьмем произвольный набор значений атрибутов, который принадлежит данному отношению. Подставим эти значения в логическую функцию вместо соответствующих переменных. Тогда логическая функция примет определенное значение. Выберем из всех наборов значений атрибутов, принадлежащих данному отношению, все те, для которых данная функция принимает значение Истина. Такую операцию над отношением называют фильтрацией, а саму логическую функцию называют фильтром. Если отношение задано таблицей, то фильтрация приводит к отбору тех строк, в которых стоят значения атрибутов, дающих истинное значение заданной логической функции.

Как вы помните, таблицы — это основной способ представления информации в реляционных базах данных. Они и реляционными называются, потому что таблицами удобно представлять отношения, а по-английски отношение — это relation. Те, кто знаком с СУБД Access, наверняка строили фильтр с помощью бланка QBE (эскиз бланка представлен табл. 5.17).

Как видно, бланк QBE начинается строкой ПОЛЕ. В ней указываются атрибуты, по которым осуществляется либо фильтрация, либо сортировка. Ниже располагается строка СОРТИРОВКА, в которой для некоторых атрибутов указывается порядок сортировки (по убыванию или по возрастанию). Еще ниже располагается строка УСЛОВИЕ ОТБОРА и несколько строк ИЛИ (из них обычно видна только одна).

Фактически бланк QBE — это снова таблица, в клетках которой для атрибута указываются операции сравнения и значения, с которыми сравниваются значения атрибута. Каждая клетка, тем самым, представляет простейшее логическое выражение или его отрицание, только имя атрибута вынесено как заголовок столбца. Выражения из клеток, стоящих в одной строке, соединяются операцией И, т.е. каждая строка — это некоторое сложное логическое выражение. А вот между собой эти “строковые” выражения соединяются уже союзом ИЛИ, о чем и напоминает слева от строки стоящее слово. Таким образом, на приведенном в качестве примера бланке QBE первая строка задает логическое выражение (Вес > 90 И Имя = Вася). Вы, конечно, вправе спросить, откуда взялся знак “=”, связывающий атрибут Имя со значением Вася. Ответ прост: разработчики Access для облегчения жизни пользователю разрешили его не писать на этом бланке (но и не запретили его писать!). Для второй строки получается выражение (Вес Ј 3 И Имя = Мария). Теперь эти два выражения надо соединить союзом ИЛИ.

Теперь, мы надеемся, вам понятно, что на бланк QBE вы специальным образом записывали некоторый предикат (без кванторов!), в котором имена атрибутов — это имена переменных, с помощью союза И в нем соединены атомарные отношения, стоящие в одной строке, а получившиеся таким образом сложные выражения соединяются союзом ИЛИ. Итак, на бланке QBE записывается не что иное, как логическое выражение. И обратите внимание, что представлено оно в дизъюнктивной нормальной форме, — чтобы это увидеть, достаточно “списать” его с бланка QBE по указанным правилам. Напомним (см. § 17), что любое сложное логическое выражение может быть записано через простые с помощью дизъюнктивной нормальной формы. Так что фильтр в СУБД Access — это фактически бескванторное логическое выражение, записанное в дизъюнктивной нормальной форме. Правда, далеко не любое. У него в каждом атомарном предикате слева стоит одна переменная (атрибут), а справа — некоторая константа или выражение без переменных.

Наверное, у вас возник вопрос — почему в языке логических выражений СУБД Access отсутствуют кванторы? Ответ таков. В любой базе данных, созданной с помощью данной СУБД, присутствует лишь конечное число значений любого атрибута. Представим, что у некоторого атрибута х множество всех его значений — это а₁, а₂, …, а_n. Легко понять, что тогда для любого предиката Р(x, y₁,
y₂, …, y_n) выражение х (Р(x, y₁, y₂, …, y_n)) равносильно конъюнкции Р(а₁, y₁, y₂, …, y_k) и Р(а₂, y₁, y₂, …, y_k) и … и Р(а_n, y₁, y₂, …, y_k), а выражение
х (Р(x, y₁, y₂, …, y_n)) равносильно дизъюнкции Р(а₁, y₁, y₂, …, y_k) или Р(а₂, y₁, y₂, …, y_k) или … или Р(а_n, y₁, y₂, …, y_k). Так что в кванторах нужды нет.

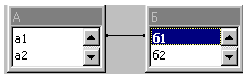
Однако это не вся правда о СУБД Access.

Обратимся к нашему “телефонному” примеру. Как мы уже обсуждали, в базе данных телефонной станции, конечно, имеется таблица, в которой указано, кто именно является абонентом данного телефонного номера (табл. 5.10). Она обновляется нечасто. Кроме того, обязательно имеется таблица совершенных телефонных звонков (табл. 5.11), которая постоянно обновляется. Имеются еще таблицы, содержащие сведения об оплате телефонных разговоров их владельцами, о выставлении счетов и т.д. Иметь все эти сведения в одной таблице не только неудобно, но и неэффективно, поскольку ее объем будет огромен. Но вот наступает момент, когда надо выписать абонентам счета за текущий месяц. Теперь надо по таблице вызовов через номер телефона определить абонента и записать в счет все относящиеся к нему вызовы. На языке отношений это можно выразить так.

Пусть S(x, y, z) — отношение, показывающее, что по телефону с номером х был разговор с пунктом у продолжительностью z минут, а А(х, v) — отношение, показывающее, что v является владельцем телефона с номером х. Нам же нужно отношение М(v, у, z), показывающее, что абонент v разговаривал с пунктом у в течение z минут. Отношение М определяется так: имеет место отношение М(v, у, z), если существует х, для которого S(x, y, z) и А(х, v). В этом случае говорят, что М(v, у, z) является произведением отношений S(x, y, z) и А(х, v).

Как видите, появился квантор существования. Поскольку Access — многотабличная СУБД, то в ней приходится выполнять операцию умножения отношений. Правда, в документации к этой СУБД такая операция называется соединением таблиц. Поскольку Access имеет графический интерфейс, то установление соединения таблиц по нужным атрибутам производится с помощью мышки “протягиванием веревочки” между этими атрибутами. На рисунке показана такая связь между атрибутами а1 и б1 двух таблиц (одна названа нами А, другая Б).

Рис. 18. Связь между атрибутами (полями) а1 и б1

Если об атрибутах ничего не сказано (как было в нашем случае), то связь выглядит именно так. Если же какой-либо атрибут объявлен ключом (см. § 34), то около него появляется цифра 1, а на другом конце появится значок “”. Это означает, что каждая строка таблицы А может оказаться связанной с несколькими строками таблицы Б, но каждая строка таблицы Б связана ровно с одной строкой таблицы А. Такую связь таблиц называют связью по типу “один ко многим”. Если же оба атрибута объявлены ключевыми, то на обоих концах появляются 1, которые означают, что в обеих таблицах каждая строка связана ровно с одной строкой из другой таблицы. Такую связь называют связью по типу “один к одному”. Разумеется, чтобы атрибут можно было объявить ключом, нужно, чтобы он удовлетворял требованиям, сформулированным в § 21.

Вопросы и ответы

1. Объясните, почему в языке логических выражений, на котором в СУБД Access записываются запросы на фильтрацию, не нужны кванторы.

2. Даны отношения нагрузка_учителей(фамилия:, класс_и_предмет:) и расписание(класс_и_предмет:, день_недели:, номер_урока:). Какую информацию несет произведение этих отношений?

3. Пусть множество М состоит из чисел 1, 2, 3, 4, 5 и 6. На этом множестве заданы следующие отношения:

а) R1(х, у): число х делится на число у;

б) R2(y, z): числа y и z таковы, что | y – z | < 3.

Найдите произведение отношений R1 и R2. (Совет: воспользуйтесь таблицами, составленными вами при выполнении задания 4 из § 20.)

4. Для каких целей используется соединение таблиц в СУБД Access?

5. Каким свойством обладает связь атрибутов разных таблиц, если оба атрибута являются ключевыми?