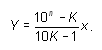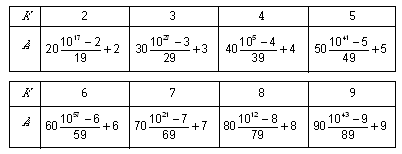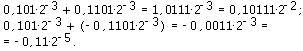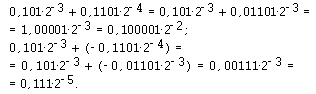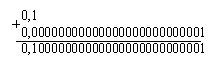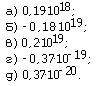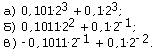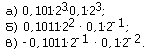Курсы повышения квалификации

Математические основы информатики

А.Г. Гейн

Учебный план

Лекция 7. Компьютерная теория чисел

Теория чисел и геометрия… Два раздела математики, которые издревле придавали ей дух игры высокого интеллекта, в которой царствовала красота логических построений. На, казалось бы, невинный и естественный вопрос ученика “Какая польза от геометрии?” Евклид велел рабу дать ученику монету и прогнать его. “Он ищет пользу в геометрии!” — с возмущением ответствовал Евклид.

Бесполезность для народного хозяйства теории чисел представляется еще более очевидной. Ну кому, скажите, стало легче жить после того, как был получен ответ на вопрос, имеет ли решение в натуральных числах уравнение xⁿ + yⁿ = zⁿ, если n > 2? А ведь этот вопрос, известный как Великая проблема Ферма, волновал математиков более 300 лет. И даже доказанный еще Евклидом факт, что простых чисел бесконечно много, вряд ли способен помочь увеличению национального валового продукта.

Другое дело компьютер. Вещь, без сомнения, полезная. Правда, ограниченная. И количество ячеек памяти, хоть и большое, но конечное. И разрядность каждой ячейки тоже конечна. Так что числа типа или p в силу своей иррациональности в компьютер “не помещаются”. А как увидеть на экране компьютера бесконечную прямую? А если прямых две, и на глаз они выглядят как параллельные? А вдруг точка пересечения все-таки есть, но где-то далеко-далеко?

Конечное и бесконечное, рациональное и иррациональное — вот противоположности, представленные в математике ярко, можно сказать, в обнаженном виде. Иррациональное и бесконечное завораживает, как взгляд в бездонные глубины космоса или в основы мироздания. Это то, что недоступно ощущению, а подвластно только разуму. И маленький ограниченный компьютер, каким бы мощным он ни был, кажется здесь бесполезным.

В 1742 г. Гольдбах в письме к Эйлеру высказал гипотезу, что каждое нечетное число, начиная с 7, представимо в виде суммы трех простых чисел. Почти 200 лет решение проблемы не удавалось сдвинуть с мертвой точки. В 1934 г. академик И.М. Виноградов доказал, что существует некоторое число N, такое, что все нечетные числа, большие чем N, представимы в виде суммы трех простых чисел. Причем это число N было вычислено (К.Бороздкин): N = ее16,038. Оно имеет всего-навсего 4 008 659 цифр. И никакой бесконечности. Достаточно проверить утверждение для всех нечетных чисел, меньших N, и проблема Гольдбаха будет решена. Человеку такое, конечно, не под силу. Но, к сожалению, и компьютерным системам пока эта задача не по зубам.

Во второй половине XX века накопилось немало теорем теории чисел, которые утверждают, что все хорошо, начиная с некоторого N, т.е. там, далеко, где нас нет. И дотянуться до этой границы простым применением компьютера мы, увы, не можем. Получилось так, что теория чисел стала поставщиком задач, экстремальных для компьютера по объемам памяти, по быстродействию, по эффективности разрабатываемых алгоритмов. Кроме того, для математиков необходимо доказательство, что созданная компьютерная программа работает правильно. А ведь вручную результаты не перепроверишь. Потребовалась разработка весьма тонких методов доказательства правильности алгоритмов и программ (заметим, что это, вообще говоря, не одно и то же). О некоторых таких методах мы рассказывали в лекции 3. Здесь же мы расскажем, как математики помогают обуздать бесконечность и иррациональность.

Можно сказать, что эта лекция о содружестве чистой математики и компьютерной науки.

§ 24. Использование компьютера в теоретико-числовых исследованиях

Приведенные выше общие рассуждения о применении компьютерных вычислений в доказательстве математических утверждений, наверно, достаточно прозрачны. Тем не менее представляется полезным увидеть, как реально они воплощаются. Мы, конечно, не возьмемся решать ту или иную знаменитую теоретико-числовую проблему, а продемонстрируем это на не очень сложной задаче.

Задача 1. Верно ли, что для любой цифры N, отличной от нуля, существует натуральное число, оканчивающееся на цифру N и такое, что ее перенос в начало числа приводит к увеличению числа в N раз?

При N = 1 положительный ответ очевиден: годится любое число, составленное из более чем одной 1, например, 11. А как обстоит дело с другими значениями N?

Ненулевых цифр совсем немного, можно попытаться получить ответ для каждой из них. Начнем с N = 2. Число оканчивается на 2, и после переноса этой цифры в начало должно получиться в 2 раза большее число, и потому оно оканчивается на 4. Значит, исходное число оканчивается на 42. Тогда после переноса цифры 2 в начало должно получиться число, оканчивающееся на 84. Значит, исходное число оканчивается на 842. Продолжая рассуждение, получаем, что предшествующая цифра 6. Процесс пошел. Но где гарантия, что он закончится?

Если у читателя хватит терпения, то он убедится, что в данном случае его ждет счастливое завершение — на семнадцатом шаге получится число 105 263 157 894 736 842, удовлетворяющее требованиям задачи.

Описанный выше процесс нетрудно запрограммировать, но сколько времени ждать ответ? А вдруг для некоторого N такого числа не существует? Тогда программа будет работать вечно¹.

И снова на помощь приходится призвать математику. Во-первых, изменим немного условие задачи, предложив рассматривать более общую ситуацию².

Задача 2. Известно, что число увеличивается в K раз от перестановки последней цифры в начало. При каких K это может происходить? Для каждого такого K найти наименьшее число, удовлетворяющее данному условию.

В этой задаче в отличие от задачи 1 не требуется, чтобы само число тоже начиналось на K; более того, натуральное число K не обязано быть цифрой.

Решение. Обозначим через A исходное число, через B — число, получающееся из A перестановкой последней цифры в начало. Тогда K = B/A. Случай K = 1 интереса не представляет, поскольку тогда A = B и наименьшее число, как мы отмечали, равно 11. (Заметим, между прочим, что и в этом случае переставляемая цифра совпадает с K.) Поэтому в дальнейшем будем считать, что K 2.

Прежде всего разберемся, сколькизначным может быть K. Поскольку числа B и A имеют одно и то же количество цифр, отношение B к A не превосходит 9. Так что K 9 (т.е. можно сказать, что само K всегда является “цифрой”).

Пусть X — последняя цифра числа A (она же первая цифра числа B), а Y — число, образованное всеми цифрами числа A, кроме последней. Пусть также n — количество цифр в числе Y. Тогда A = 10 · Y + X, а B = X · 10ⁿ + Y. Тем самым, получаем равенство:

X · 10ⁿ + Y = K(10 · Y + X),

откуда

.

Знаменатель 10K – 1 всегда двузначен. Вот какие значения он принимает:

В третьей строке этой таблицы приведено в виде несократимой дроби значение множителя перед X при n = 1. Это означает, что ни для какой цифры X при n = 1 значение Y не получается целым. Значит, n 2.

Тот факт, что Y имеет в записи n цифр, означает, что 10^n–1 Y < 10n. Отсюда для X получаем двойное неравенство:

.

Левая часть этого неравенства легко преобразуется к виду:

.

Поскольку n 2 и K 9, дробь (10n–1 – K) : (10n – K) положительна и меньше 1. Учитывая, что X – целое число, левую часть неравенства можно записать K X.

Займемся теперь правой частью этого неравенства. Аналогичные преобразования показывают, что она равна

.

Поскольку K 9 и n 2, дробь 9K / (10ⁿ – K) положительна и меньше 1. Учитывая, что X — целое число, правую часть неравенства можно записать X  10K – 1. Впрочем, это неравенство нам мало что дает, поскольку по условию X и так меньше 9.

Итак, мы выяснили, что перемещаемая цифра не может быть меньше, чем K. Так что в задаче 1 просто взято наименьшее возможное значение для перемещаемой цифры.

Теперь займемся главным вопросом задачи 2: при каких же K найдется такое n, что число Y окажется целым? Иными словами, для каких K существует n, при котором 10ⁿ – K делится на 10K – 1? Здесь мы воспользуемся следующей идеей. Для удобства дальнейших рассуждений обозначим число 10K – 1 буквой m. Ясно, что число m не имеет с числом 10 общих делителей, отличных от 1. В частности, никакая степень числа 10 не делится на m без остатка.

Рассмотрим последовательность степеней числа 10:

1 = 10⁰; 10¹; 10²; 10³; ...; 10^m-1,

и последовательность остатков от деления этих чисел на m. Все эти остатки, как было сказано, отличны от нуля. Однако различных ненулевых остатков при делении на m всего лишь m – 1. Значит, в данной последовательности степеней найдутся два числа с одинаковыми остатками при делении на m. Пусть это 10^a и 10^b, где
0 a < b m – 1. Тогда 10^b – 10^a делится на m. Но 10^b – 10^a = 10^a (10^b-a – 1), а число m не имеет с числом 10 неединичных общих делителей. Поэтому на m в этом произведении делится число 10^b-a – 1. Обозначим b – a через t.

Таким образом, нами доказано, что найдется такой положительный показатель степени t m – 1, что 10^t – 1 делится на m. Мы можем считать, что t выбрано наименьшим с тем свойством, что 10^t – 1 делится на m. Иными словами, среди степеней 10¹; 10²; 10³; ...; 10^t-1 ни одна не дает остаток 1 при делении на m. А начиная с 10t остатки будут повторяться в той же последовательности. Тем самым, никаких других остатков при делении на m степеней числа 10, кроме тех, которые встречаются в ряду 1 = 10⁰; 10¹; 10²; 10³; ...; 10^t-1, нет. Чтобы на m делилось число 10ⁿ – K, нужно K иметь остатком при делении подходящей степени числа 10 на m. А выяснить это можно, составив несложный циклический алгоритм, поскольку известно, какое наибольшее число степеней придется рассматривать, чтобы понять, встретится ли нужный остаток: не более чем m – 1. Вот соответствующий алгоритм:

алг задача_2 (арг цел K)

дано 2 K 9

надо | напечатать показатель степени числа 10,

| дающей в остатке K при

| делении этой степени на 10K–1.

нач цел X, N

X := 1

N := 0

M := 10*K–1

нц пока не (X = K или N = M)

X := mod(10*X, M)

N := N + 1

кц

если X = K

то вывод N

иначе вывод "Такой степени нет"

все

кон

Результаты работы этого алгоритма представлены в следующей таблице:

Поскольку ни при каком допустимом значении K алгоритм не выдал сообщение об отсутствии подходящей степени, мы доказали следующую теорему:

Теорема. Для каждого натурального K 9 существует число, которое увеличивается в K раз от перестановки последней цифры в начало.

Обратите внимание, как при доказательстве данной теоремы применялся компьютер. Во-первых, сначала была доказана конечность числа вариантов, подлежащих перебору, во-вторых, с помощью составленного алгоритма мы искали не само число, а проверяли выполнение некоторого условия, необходимого и достаточного для существования числа с нужным свойством.

Впрочем, пользуясь полученной таблицей, легко указать и сами числа с требуемым свойством — в качестве X надо взять K и воспользоваться полученной формулой для Y, чтобы найти требуемое там число A:

Желающие могут получить теперь и запись числа A цифрами (например, при K = 5 число А = 510 204 081 632 653 061 224 489 795 918 367 346 938 775; а самое длинное число получается при K = 6 — оно содержит 58 цифр).

Заметим, что не все приведенные ответы к задаче 1 являются ответами к нашей задаче 2: при K = 5 (и только при этом значении K)³ найдется меньшее число, удовлетворяющее условию задачи. Это число получается, если X взять равным 7. Тогда нужно будет разыскать степень числа 10, дающую в остатке 5 при делении не на 49, а всего лишь на 7. Показатель такой степени равен 5. Искомое число в этом случае 10(10⁵ – 5) / 7 + 7 = 142 857. Это число просто “малютка” в сравнении с приведенным выше 42-значным числом, которое получается как ответ к задаче 1.

Конечно, это всего лишь демонстрация того, как компьютер может применяться к доказательству теоремы. На самом деле если поразмышлять еще немного, то можно доказать следующее утверждение: если 10^t – 1 делится на 10K – 1, то 10^t-1 при делении на 10K – 1 обязательно дает остаток K. Тем самым, в доказательстве теоремы можно было обойтись и без компьютера. Однако на сегодняшний день существует целый ряд математических утверждений, доказательство которых без компьютера пока получить не удается. Вот только один пример. Давно известно (с XVII века) и нетрудно доказать средствами школьной алгебры, что число 2ⁿ – 1 может быть простым лишь при условии, что само число n является простым. Числа вида 2ⁿ – 1 получили даже специальное название — числа Мерсенна — по имени средневекового монаха, обратившего внимание математиков на эти числа⁴. К сожалению, обратное утверждение неверно: не каждое число вида 2ⁿ – 1 при простом n является простым. Например, число 2¹¹ – 1 = 2047 = 23 · 89 является составным. И хотя неизвестно, бесконечно ли много простых чисел Мерсенна, они и сегодня служат одним из источников больших простых чисел. До изобретения компьютеров самым большим известным простым числом Мерсенна было число 2¹²⁷ – 1, имеющее 39 цифр. И это было вообще самое большое известное в то время простое число. Появление компьютеров сразу увеличило наше знание простых чисел Мерсенна. Уже в 1952 году были обнаружены сразу 5 простых чисел: 2⁵²¹ – 1; 2⁶⁰⁷ – 1; 2¹²⁷⁹ – 1; 2²²⁰³ – 1; 2²²⁸¹ – 1. Последнее из них имеет 687 цифр; даже для современных компьютеров разложение такого числа на множители — дело весьма напряженное. Выход из этой сложной ситуации состоит в том, что для доказательства простоты числа Мерсенна используется так называемый “критерий Люка”. Он заключается в следующем. Для выбранного простого числа р рекуррентно строится последовательность s₁, s₂, s₃, …, s_n, где s₁ = 4, а s_k+1 — остаток при делении на числа – 2 на р. Если s_p-1 = 0, то число 2р – 1 простое. Так, для р = 2281 проводить вычисления приходится не более чем с семизначными числами (ибо 2280² = 5 198 400), а это можно сделать в самой обычной компьютерной арифметике. Ситуация вполне аналогичная той, которая была у нас при решении задачи 1, — вместо того, чтобы искать 58-разрядное число при K = 6, мы подобрали иную форму записи такого числа и обошлись вычислениями не более чем с двузначными числами.

§ 25. Математика компьютерной арифметики

Уже в предыдущем параграфе мы несколько раз упомянули о трудностях компьютерных вычислений, связанных с ограниченностью разрядной сетки. Что стоит за этими словами?

Физически память компьютера — это пронумерованная совокупность ячеек. В свою очередь, каждая ячейка состоит из восьми устройств, каждое из которых может находиться в одном из двух состояний. Одно из состояний кодируется символом 0, а другое — символом 1. Тем самым, в одной ячейке размещается 1 байт информации.

Содержимое каждой ячейки, если отбросить возможно стоящие в ней первые нули, можно рассматривать как запись натурального числа в двоичной системе счисления. При этом коду 00000000 сопоставляется число 0.

Легко подсчитать, что такое кодирование позволяет записать целые числа от 0 до 255 включительно. Ведь самое большое число — это 1111111112 =  2⁸ – 1 = 255.

Однако, кроме положительных целых чисел, существуют отрицательные. Чтобы указать знак числа, нужен еще один бит. При этом договариваются, что его нулевое значение соответствует знаку “+”, а единичное значение — знаку “–”. Обычно под знак выделяют самый левый бит ячейки. Тогда код наибольшего натурального числа, которое можно записать в одной ячейке, — это 01111111. Ему соответствует десятичное число +127. А код наименьшего отрицательного числа — это 111111111; в десятичной записи ему соответствует число –127.

Чтобы найти сумму чисел 101₂ и 1011₂ , с их кодами можно действовать по правилам сложения двоичных чисел: 00000101 + 00001011 = 00010000. Но попытка по тем же правилам сложить коды чисел 1010101₂ и 111101₂ приведет к странному результату: 01010101 + 00111101 = 100100010. Результат оказался отрицательным числом!

Каждому ясно: ошибка возникла из-за того, что разрядная сетка ячейки содержит всего семь мест. Впрочем, если ячейка имела бы и больше разрядов, все равно такая ошибка возникнет каждый раз, как потребуется найти сумму достаточно больших чисел.

Описанное выше явление называется эффектом переполнения. И о нем приходится помнить, когда имеешь дело с достаточно большими целыми числами.

Попытаемся теперь сложить положительное число с отрицательным. Например, число 1010₂ с числом –101₂ . Их коды, соответственно, таковы: 00001010 и 10000101. А результатом должно быть натуральное число 101₂ . Даже сам алгоритм получения кода результата сформулировать не так уж просто (попытайтесь, ради интереса, такое проделать), а тем более реализовать простое устройство, которое бы этот алгоритм исполняло. А ведь сложение компьютеру приходится выполнять довольно часто, так что все должно быть как можно проще и быстрее.

Для того чтобы выполнение операции сложения было проще и не зависело от знака слагаемых, отрицательные целые числа кодируют другим способом. Но сначала поговорим о нуле.

Что будет, если в восьмиразрядную ячейку попытаться записать натуральное число 100000000₂ ? Все восемь разрядов окажутся нулями. Значит, компьютер воспринимает это число как 0. Этим-то мы и воспользуемся. Вычтем из числа 100000000₂ число 101₂ . Получится 11111011₂ . Если теперь это число сложить с числом 101₂ , то компьютер воспримет результат как 0. Поэтому число 11111011₂ естественно объявить кодом отрицательного числа –101₂ . Его называют дополнительным кодом данного отрицательного числа.

Об одном коде поговорим отдельно. Рассмотрим код 10000000. Во-первых, это код отрицательного числа, поскольку в самом левом разряде стоит 1. Компьютер воспринимает его как дополнительный код. Тогда прямой код противоположного ему положительного числа совпадает с разностью 100000000₂ – 10000000₂ . Она равна 10000000, т.е. 128₁₀. Таким образом, наименьшее отрицательное число, которое можно записать в восьмибитовую ячейку, — это –128.

Кодом числа 0 является 00000000. А что произойдет, если записать дополнительный код для числа –0? Вычитаем из 100000000₂ число 0₂ и получаем 10000000₂  . При записи в ячейку снова окажется 00000000. Так что компьютер, как и мы с вами, не различает числа +0 и –0.

Конечно, для вычисления дополнительного кода отрицательного числа n можно каждый раз вычитать из 100000000₂ модуль числа n. Но есть и другой способ. Вот как можно поступать, чтобы получить дополнительный код отрицательного числа:

1. Записать двоичный код модуля числа.

2. В полученной записи каждую цифру 1 заменить цифрой 0, а каждую цифру 0 — цифрой 1.

3. К полученному коду, рассматриваемому как натуральное число в двоичной системе, прибавить 1.

Как видите, построение дополнительного кода осуществляется легко. И поскольку вычитание можно заменить сложением с противоположным числом, переход к дополнительному коду числа позволяет вообще обойтись без вычитания.

Конечно, диапазон от –128 до +127 во многих случаях маловат для решения возникающих задач. Но вовсе не обязательно хранить целое число ровно в одной восьмибитовой ячейке. Обычно для целых чисел отводится две ячейки — именно так происходит, если вы объявляете тип переменной Integer. Если же объявить тип LongInt, то под целое число будут отведены 4 восьмибитовые ячейки. А вот одна ячейка отводится, если объявлен тип ShortInt.

Если под запись числа отведено две ячейки, то они воспринимаются как единое целое. Принцип же кодирования тот же: самый левый разряд отводится под знак числа, остальные пятнадцать разрядов — для кода абсолютной величины числа. Для положительных чисел используется прямой код, для отрицательных — дополнительный. Тем самым, диапазон целых чисел таков: от –32 768 до +32 767 = 2¹⁵ – 1.

Вообще, если для записи целых чисел используется m-битный двоичный код, то диапазон кодируемых чисел от –2^m–1 до 2^m–1 – 1, при этом дополнительный код отрицательного числа n из этого диапазона совпадает с записью в двоичной системе числа 2^m + n.

Ясно, что при умножении целых чисел эффект переполнения возникает еще чаще. А как на это реагирует компьютер? Переполнение при выполнении операций с числами, записанными с фиксированной запятой, не вызывает прерывания работы процессора. В зависимости от используемого языка диагностика может отсутствовать (так, например, происходит при использовании большинства версий языка Турбо Паскаль), может сообщать пользователю о данном событии и ждать его реакции, а может просто переходить к записи числа с плавающей запятой (так бывает в различных версиях языка Бейсик).

Конечно, кроме целых чисел, человек активно пользуется дробями. И любое вещественное число может быть записано конечной или бесконечной десятичной дробью. Впрочем, такое представление нужно бывает, как правило, лишь в теоретических построениях. А на практике...

На практике в большинстве случаев приходится иметь дело именно с приближенными значениями величин. Приближенные значения возникают при измерениях, при подсчете больших величин, да и во многих других случаях. Поэтому исследователь или инженер, решая ту или иную задачу, должен изначально оценить, сколько значащих цифр следует иметь в ходе проводимых им вычислений и сколько оставить в результате. Но об этом речь обычно идет в курсе математики. Мы же сейчас хотим обратить ваше внимание на другое.

Допустим, решено, что достаточно трех значащих цифр. Тогда в числах, скажем, 37 200 000; –372; 3,72; 0,000372 нам требуется знать лишь эти три цифры и то, начиная с какого десятичного разряда они записаны. Именно такую информацию и надо сообщить компьютеру. Для этого представим числа единообразно: пишем 0 (а перед ним знак “–”, если число отрицательно), затем запятую, сразу после запятой пишем значащие цифры и получившуюся десятичную дробь умножаем на подходящую степень числа 10. Вот что получится для четырех указанных выше чисел:

37 200 000 = 0,372 ·10⁸;

–372 = –0,372 · 10³;

3,72 = 0,372 · 10¹;

0,000372 = 0,372 · 10^–3.

Ясно, что абсолютную величину любого числа можно представить как произведение числа, заключенного между 0,1 и 1, и степени числа 10 с целым показателем. Дробная часть первого множителя в таком представлении называется мантиссой числа, а показатель степени числа 10 — порядком числа. Само представление числа в виде такого произведения называется нормализованной записью числа. По-другому такое представление чисел называют записью чисел с плавающей запятой. Максимально допустимое количество разрядов в мантиссе числа определяет точность, с которой данное число может быть представлено.

В компьютере числа представлены в двоичной системе счисления. Для двоичной системы нормализованный вид числа — это представление его в виде ±m·2^p, где 0,1₂ m < 1, а р — целое число. Например,

0,1₁₀ = 0,0(0011)₂ = 0,11(0011) · 2^–3.

Число с плавающей запятой в памяти компьютера может занимать разное количество байтов. Для записи числа, как говорят, с обычной точностью отводится 4 байта, а числа двойной точности занимают 8 байтов. Впрочем, в зависимости от конструкции компьютера встречаются и другие варианты, например, когда под запись числа отводится 10 байтов.

В большинстве практических случаев того, что называют обычной точностью представления действительных чисел, оказывается вполне достаточно. Поэтому и мы дальше рассмотрим только этот случай. В нем под знак числа и порядок отводится
1 байт, и это первые 8 разрядов. Остальные 24 разряда отводятся под мантиссу. Это, например, означает, что мантисса компьютерного представления числа 0,1₁₀ будет такова:

110011001100110011001101

Знак числа кодируется обычным образом: “плюс” кодируется символом 0, “минус” — символом 1. Что касается порядка числа, то там записывается так называемый машинный порядок. Под него отведено семь разрядов, и он равен целому неотрицательному числу, для которого данный код является прямым двоичным кодом. Например, коду 0101011 соответствует машинный порядок 43. Машинный порядок связан с порядком числа следующим образом:

порядок числа = машинный порядок – 2⁶.

Тем самым, цепочка 0101011 является кодом порядка, равного –21. А последовательность 0000000 кодирует порядок –64. Нетрудно видеть, что нулевой порядок кодируется как 1000000. Наибольший положительный порядок имеет код 1111111 и равен 63.

Вот как выглядит полный компьютерный код числа 0,1₁₀:

Заметим еще раз, что представление чисел с плавающей запятой в памяти компьютера может осуществляться весьма по-разному — в зависимости от языка программирования, особенностей архитектуры
и т.д. Например, в некоторых языках под мантиссу отводится всего лишь один байт и знак числа записывается при мантиссе, а не выносится в крайний левый разряд. Мы здесь продемонстрировали лишь основные принципы представления таких чисел.

Рассмотрим теперь сложение чисел с плавающей запятой. Если у чисел в нормализованном виде порядки одинаковы, то достаточно сложить мантиссы этих чисел, а затем нормализовать полученный результат, если эта сумма окажется больше 1 или меньше 0,1. Например,

Хотя примеры приведены в двоичной системе счисления, ясно, что высказанное правило действует в любой позиционной системе.

Если же порядки нормализованных чисел различны, то при сложении чисел с плавающей запятой предварительно выполняется операция выравнивания порядков слагаемых. Заметим, что величина числа не меняется при сдвиге мантиссы на один разряд вправо с одновременным увеличением порядка на 1. Поэтому в том слагаемом, у которого порядок меньше, производится сдвиг мантиссы вправо на разность между порядками, после чего мантиссы складываются, и результат снова нормализуется. Например,

Значит, можно сформулировать следующее правило сложения чисел с плавающей запятой.

Намного проще выполняется умножение и деление чисел в нормализованном виде.

Например,

0,101 · 2^–3 · 0,1011 · 2⁴ = (0,101 · 0,1011) · 2^–3+4 = 0,0110111 · 2¹ = 0,110111 · 2⁰.

Например,

0,1011 · 2^–3 : 0,101 · 2⁴ = (0,1011 : 0,101) · 2^–3–4 = 1,0001100110011...  · 2^–7 = =0,10001100110011...   · 2^–6.

Последний пример показывает, что на практике даже при обычных вычислениях мы будем вынуждены довольствоваться лишь приближенным значением дроби. В компьютере ограниченность разрядной сетки играет еще большую роль. Пусть, к примеру, мы складываем числа a = 0,1 · 2¹³ и b = 0,1 · 2^–12. После выравнивания порядков получаем:

Но в разрядную сетку для мантиссы помещается лишь 24 цифры, а не 26. Поэтому два последних разряда будут утеряны, и результат совпадет с первым слагаемым. Получается, что в “компьютерной арифметике” вполне может оказаться a + b = a, хотя b 0. И это далеко не единственная особенность компьютерной арифметики. В задании 15 приведен пример, показывающий, что может не выполняться сочетательный закон для сложения.

При умножении и делении нормализованных чисел одним из возможных эффектов является переполнение разрядной сетки для порядка числа. Вот пример:

0,1001 · 2³² · 0,11 · 2³³ = 0,011011 · 2⁶⁵ = 0,11011 · 2⁶⁴.

Но наивысший возможный порядок — это 63. Следовательно, данный результат непредставим в компьютерной арифметике. Обычно операционная система или компилятор языка программирования в таком случае дает диагностику “переполнение”. Впрочем, переполнение для нормализованных чисел может возникнуть и при сложении; в задании 17 вам предлагается построить соответствующий пример.

Кроме рассмотренных случаев, когда при вычислении на компьютере получается неверный результат или результат вообще не получается, надо иметь в виду эффекты, связанные с округлением чисел. Эти эффекты также обусловлены ограниченностью разрядной сетки. Одним из них является потеря значащих цифр. Возьмем, к примеру, числа 1/1000 и 1/1004. В двоичной системе счисления в нормализованном виде они с учетом округления равны соответственно 0,100000110001001001101111 · 2^–9 и 0,100000101000110010110000 · 2^–9. После вычитания получится 0,1000010110111111 · 2^–17. Точное значение разности равно 4/1004000. При записи в нормализованном виде с 24-разрядной мантиссой получаем 0,100001011010111011101100 · 2^–17. Как видите, только первые 11 цифр после запятой оказались точными.

Итак, компьютерная арифметика может давать следующие эффекты:

1) ошибки округления, которые возникают при записи чисел с округлением и могут накапливаться при выполнении операций;

2) переполнение разрядной сетки порядка чисел приводит к получению невоспроизводимого в компьютере числа;

3) потеря значащих цифр при вычитании близких чисел или при переполнении разрядной сетки мантиссы;

4) игнорирование слагаемого при большой разнице в порядках.

В качестве практической рекомендации отметим, что для вещественных чисел, которые представляются в компьютере в нормализованном виде, не следует сравнивать их на точное равенство; вместо этого надо сравнивать абсолютную величину их разности с подходящим маленьким положительным числом, соответствующим погрешности представления.

Вопросы и задания

1. Какова основная причина различных эффектов компьютерной арифметики?

2. Что такое дополнительный код? Каковы преимущества использования дополнительного кода?

3. Каков диапазон целых чисел, для кодирования которых используются 4 ячейки?

4. В чем состоит эффект переполнения?

5. Объясните, почему приведенный в объяснительном тексте параграфа способ действительно дает дополнительный код отрицательного числа.

6. а) Следующие целые числа записаны в прямом восьмибитном коде: 01101010; 10111011; 10001001; 01010111; 11111111. Найдите среди них отрицательные числа и запишите их в дополнительном коде.

б) Следующие числа записаны в прямом шестнадцатибитном коде:

Найдите среди них отрицательные числа и запишите их в дополнительном коде.

7. а) Выполните сложение чисел 100₁₀ и 50₁₀ в однобайтовом коде представления целых чисел с фиксированной запятой. Кодом какого числа (в десятичной системе счисления) будет полученный результат? (Совет: не забудьте, что отрицательные числа представляются в дополнительном коде.)

б) Выполните сложение чисел –80₁₀ и –64₁₀ в однобайтовом коде представления целых чисел с фиксированной запятой. Кодом какого числа (в десятичной системе счисления) будет полученный результат?

8. Почему при компьютерном сложении целых чисел может нарушаться сочетательный закон
(a + b) + c = a + (b + c)? Для обоснования ответа приведите подходящий пример.

9. Какую запись числа называют нормализованной? Что такое мантисса и порядок числа?

10. Каким будет первый символ кода машинного порядка числа, если порядок числа, представленного в двоичном нормализованном виде, неотрицателен?

11. В объяснительном тексте параграфа приведена четырехбайтовая запись числа 0,1₁₀ в памяти компьютера.

а) Какому десятичному числу на самом деле соответствует эта запись?

б) Каковы абсолютная и относительная погрешности представления числа 0,1₁₀?

в) Объясните, почему последней цифрой мантиссы оказалась цифра 1.

12. Укажите, какие из нижеприведенных действительных чисел могут быть представлены в памяти компьютера четырехбайтовым кодом числа с плавающей запятой, описанным в объяснительном тексте.

13. Выполните сложение двоичных чисел, представленных в нормализованном виде. Результат нормализуйте.

14. Выполните умножение двоичных чисел, представленных в нормализованном виде. Результат нормализуйте.

15. По правилам компьютерной арифметики вычислите суммы

Убедитесь, что для этих чисел нарушается сочетательный закон.

16. Объясните, почему при умножении чисел с плавающей запятой может нарушаться сочетательный закон. Приведите подтверждающие примеры.

17. Приведите пример двух нормализованных двоичных чисел, при сложении которых может произойти переполнение.

18. Для решения некоторой задачи Петя составил следующий алгоритм:

алг Сумма1 (арг цел N, рез вещ: S)

нач цел: K

ввод N

S := 0

нц для K от 1 до N

S := S + 1/K

кц

вывод S

кон

В свою очередь, Коля для решения той же задачи составил такой алгоритм:

алг Сумма2 (арг цел N, рез вещ: S)

нач цел: K

ввод N

S := 0

нц для K от N до 1 с шагом –1

S := S + 1/K

кц

вывод S

кон

а) Верно ли, что оба алгоритма решают одну и ту же задачу?

б) Верно ли, что при N = 1 000 000 000 программы, реализующие данные алгоритмы, дадут одинаковый результат, если используется четырехбайтовое представление нормализованных чисел, описанное в тексте параграфа?

¹ Вечно она, конечно, работать не будет — или произойдет переполнение памяти компьютера в ходе вычисления все новых и новых цифр, или Чубайс свет вырубит…

² Этот прием достаточно хорошо известен математикам, но весьма редко используется в программировании.

³ Между прочим, доказательство этого утверждения — о том, что при других значениях K нет решений задачи 2, не совпадающих с решением задачи 1, — автор статьи без компьютера получать не умеет.

⁴ Впрочем, история математики так же изобилует белыми пятнами, как и любая другая история. Некоторые исследователи считают, что простыми числами Мерсенна интересовались уже пифагорейцы в связи с так называемыми “совершенными числами”.