СЕМИНАР

С.Б. Гашков,
Москва

Системы счисления и их применения*

Продолжение. Начало в № 2/2006.

§ 4. Краткая история двоичной системы

Некоторые идеи, лежащие в основе двоичной системы, по существу были известны в Древнем Китае. Об этом свидетельствует классическая книга “И цзин” (“Книга перемен”), о которой речь пойдет позже.

Идея двоичной системы была известна и древним индусам.

В Европе двоичная система, видимо, появилась уже в новое время. Об этом свидетельствует система объемных мер, применяемая английскими виноторговцами: два джилла = полуштоф, два полуштофа = пинта, две пинты = кварта, две кварты = потл, два пот-ла = галлон, два галлона = пек, два пека = полубушель, два полубушеля = бушель, два бушеля = килдеркин, два килдеркина = баррель, два барреля = хогзхед, два хогзхеда = пайп, два пайпа = тан.

Читатели исторических романов, видимо, знакомы с пинтами и квартами. Частично эта система дожила и до нашего времени (нефть и бензин до сих пор меряют галлонами и баррелями).

И в английских мерах веса можно увидеть двоичный принцип.

Так, фунт (обычный, не тройский) содержит 16 унций, а унция — 16 дрэмов. Тройский фунт содержит 12 тройских унций. В английских аптекарских мерах веса, однако, унция содержит восемь дрэмов.

Пропагандистом двоичной системы был знаменитый Г.В. Лейбниц (получивший, кстати, от Петра I звание тайного советника).

Он отмечал особую простоту алгоритмов арифметических действий в двоичной арифметике в сравнении с другими системами и придавал ей определенный философский смысл. Говорят, что по его предложению была выбита медаль с надписью: “Для того чтобы вывести из ничтожества все, достаточно единицы”. Известный современный математик Т.Данциг о нынешнем положении дел сказал: “Увы! То, что некогда возвышалось как монумент монотеизму, очутилось в чреве компьютера”. Причина такой метаморфозы не только уникальная простота таблицы умножения в двоичной системе, но и особенности физических принципов, на основе которых работает элементная база современных ЭВМ (впрочем, за последние 40 лет она неоднократно менялась, но двоичная система и булева алгебра по-прежнему вне конкуренции).

§ 5. Почему двоичная система удобна?

Главное достоинство двоичной системы — простота алгоритмов сложения, вычитания, умножения и деления. Таблица умножения в ней совсем не требует ничего запоминать: ведь любое число, умноженное на ноль, равно нулю, а умноженное на единицу равно самому себе. И при этом никаких переносов в следующие разряды, а они есть даже в троичной системе. Таблица деления сводится к двум равенствам 0/1 = 0, 1/1 = 1, благодаря чему деление столбиком многозначных двоичных чисел делается гораздо проще, чем в десятичной системе и, по существу, сводится к многократному вычитанию.

Таблица сложения, как ни странно, чуть сложнее, потому что 1 + 1 = 10 и возникает перенос в следующий разряд. В общем виде операцию сложения однобитовых чисел можно записать в виде x + y =  2w + v, где w, v — биты результата. Внимательно посмотрев на таблицу сложения, можно заметить, что бит переноса w — это просто произведение xy, потому что он равен единице лишь когда x и y равны единице. А вот бит v равен x + y, за исключением случая x = y = 1, когда он равен не 2, а 0. Операцию, с помощью которой по битам x, y вычисляют бит v, называют по-разному. Мы будем использовать для нее название “сложение по модулю 2” и символ . Таким образом, сложение битов выполняется фактически не одной, а двумя операциями.

Если отвлечься от технических деталей, то именно с помощью этих операций и выполняются все операции в компьютере.

Для выполнения сложения однобитовых чисел делают обычно даже специальный логический элемент с двумя входами x, y и двумя выходами w, v, как бы составленный из элемента умножения (его часто называют конъюнкцией, чтобы не путать с умножением многозначных чисел) и элемента сложения по модулю 2. Этот элемент часто называют полусумматором.

§ 6. Ханойская башня, код Грея и двоичный n-мерный куб

Далее мы рассмотрим несколько интересных задач, в решении которых помогает знание двоичной системы. Начнем мы с задач, в которых используется только одна, самая простая из лежащих в ее основе идей — идея чисто комбинаторная и почти не связанная с арифметикой.

Первая из них — это “Ханойская башня”. Головоломку под таким названием придумал французский математик Эдуард Люка в XIX веке.

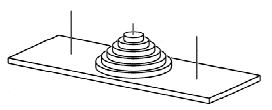
Рис. 2

На столбик нанизаны в порядке убывания размеров n круглых дисков с дырками в центре в виде детской игрушечной пирамидки. Требуется перенести эту пирамидку на другой столбик, пользуясь третьим вспомогательным столбиком (рис. 2). За один ход разрешается переносить со столбика на столбик один диск, но класть больший диск на меньший нельзя. Спрашивается, за какое наименьшее количество ходов это можно сделать? Ответом в этой задаче служит уже известное нам “индийское число” 2ⁿ – 1. Люка в своей книге приводит якобы известную легенду о том, что монахи в одном из монастырей Ханоя занимаются перенесением на другой столбик пирамидки, состоящей из 64 дисков. Когда они закончат работу, кончится жизнь Брахмы⁵. Видно, ждать придется долго.

Решение этой головоломки сильно облегчается, если знать, что такое код Грея. Кодом Грея порядка n называется любая циклическая последовательность всех наборов из нулей и единиц длины n, в которой два соседних набора отличаются ровно в одной компоненте. Примером кода Грея порядка 3 является последовательность трехразрядных наборов 000, 001, 011, 010, 110, 111, 101, 100.

9. Докажите, что длина кода Грея порядка n равна 2ⁿ.

Если занумеровать компоненты каждого набора справа налево (при этом последняя, т.е. самая правая, компонента получит номер 1) и начинать код Грея с нулевого набора, то его можно записать короче, если вместо очередного набора писать только номер компоненты, в которой он отличается от предшествующего набора. Например, указанный выше код Грея можно коротко записать в виде последовательности семи чисел 1, 2, 1, 3, 1, 2, 1. В общем случае длина подобной последовательности равна 2ⁿ – 1. Указанная краткая запись позволяет догадаться, как можно строить коды Грея дальше. Например, Грея порядка 4 можно задать последовательностью 1, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, 3, 1, 2, 1. Она получается, если мы повторим два раза последовательность, определяющую код Грея порядка 3, разделив оба экземпляра этой последовательности числом 4. Далее поступаем аналогично, т.е. последовательность длины 2ⁿ – 1, определяющую код Грея порядка n, дублируем, разделив оба дубля числом n + 1. Полученная последовательность длины 2(2ⁿ – 1) + 1 = 2ⁿ+1 – 1 будет определять код Грея порядка n + 1.

Легко видеть, что эта последовательность, так же, как и предыдущая, не изменяется, если ее выписать в обратном порядке. Последовательности (или слова) с таким свойством называются палиндромами. Например, одним из самых известных русских палиндромов является предложение (символы пробела, естественно, игнорируются)

А РОЗА УПАЛА НА ЛАПУ АЗОРА.

Нам понадобится это свойство кода Грея порядка n + 1, а также то обстоятельство, что все числа этой последовательности, кроме среднего, не больше n. Это означает, что если с ее помощью мы начнем выписывать последовательность наборов длины n + 1, начиная с нулевого, то первые 2ⁿ – 1 наборов будут начинаться с нуля, так как (n + 1)-я компонента никогда в них не будет меняться. Остальные же компоненты будут образовывать наборы длины n, и они будут чередоваться в том же порядке, что и в коде Грея порядка n, поэтому получится некоторая перестановка всех 2ⁿ наборов длины n + 1, начинающихся с нуля. Потом в ее последнем наборе этот ноль будет заменен на единицу (это определяется тем, что в середине последовательности стоит число n + 1), далее эта единица меняться не будет, а будет меняться в каждом очередном наборе длины n + 1 только одна из последних n компонент, и эти компоненты образуют код Грея порядка n, выписанный в обратном порядке, и закончится он нулевым набором. Сама же построенная при этом последовательность наборов длины n + 1 будет образовывать перестановку всех наборов длины
n + 1, начинающихся с единицы, а ее последним набором будет набор 10...0. Таким образом, построенная последовательность состоит из 2ⁿ различных наборов и может быть превращена в циклическую, т.е. является кодом Грея порядка n + 1.

Код Грея можно наглядно изобразить на n-мерном двоичном кубе. Сам этот куб служит для наглядного представления множества всех наборов длины n из нулей и единиц. Наборы изображаются точками и называются вершинами куба. Два набора, отличающиеся только в одной компоненте, называются соседними и образуют ребро куба. Номер этой компоненты называется направлением ребра. Куб можно нарисовать на плоскости так, что все ребра будут изображены отрезками, соединяющими их вершины, причем ребра одного направления будут изображены равными и параллельными отрезками (поэтому такие ребра тоже называют параллельными). Например, четырехмерный куб можно изобразить на плоскости так, как показано на рис. 3.

Рис. 3

Код Грея на многомерном кубе можно изобразить в виде последовательности вершин, в которой каждые две соседние вершины соединяются ребрами. Такие последовательности вершин принято называть путями. Но код Грея изображается путем, у которого первая и последняя вершины тоже соединяются ребром. Такие пути естественно называть циклами. Однако код Грея — не просто цикл, а цикл, проходящий через все вершины куба. Такие циклы (а их можно искать не только на многомерном кубе, но и на любом графе⁶) называются гамильтоновыми циклами⁷, а графы, у которых они есть, — гамильтоновыми графами. Вопрос о том, какие графы гамильтоновы, а какие нет, оказался чрезвычайно трудным и не решен удовлетворительно по сей день. Ему можно посвятить отдельную книгу, и такие книги уже написаны, поэтому мы прекращаем разговор на эту тему и возвращаемся к многомерному кубу.

Для того чтобы изобразить код Грея на приведенном на рис. 3 изображении n-мерного куба, рядом с вершинами следует написать их имена — соответствующие им наборы из нулей и единиц. Сделать это можно, например, таким образом. Самой нижней вершине сопоставим набор из одних нулей. Ребрам сопоставим номера их направлений, например, направлению самого правого ребра, выходящего из “нулевой” вершины, сопоставим номер 1, и т.д., а направлению самого левого такого ребра — номер n. Далее сопоставляем оставшимся вершинам куба имена с помощью следующего алгоритма. Если какой-то вершине имя уже присвоено и, поднимаясь из нее вверх по какому-нибудь ребру, скажем, направления k, попадаем в новую, пока безымянную, вершину, то ей присваиваем имя, которое получается из имени прежней вершины заменой k-й компоненты (которая была нулем) на противоположную (т.е. единицу). Если же мы попали в вершину, имя которой уже было присвоено ранее, то можно ничего не делать, так как если мы попробуем все же сопоставить ей имя согласно указанному правилу, то оно совпадет с уже присвоенным именем. Очевидно, самой верхней вершине будет присвоен набор из одних единиц. Результат работы описанного алгоритма для четырехмерного куба показан на рис. 4.

Читателю предоставляется возможность самому решить головоломку Люка и обнаружить ее связь с кодом Грея, а мы займемся другим вопросом.

На изображениях многомерного куба бросается в глаза, что все вершины, имена которых содержат заданное число единиц, скажем k, лежат на одной прямой (рис. 5). Говорят, что эти вершины лежат на k-м слое куба. Очевидно, нулевой слой состоит из одной вершины — “нулевой”, а n-й слой состоит только из “единичной” вершины.

10. Сколько различных “возрастающих” путей ведут из “нулевой” вершины в данную вершину k-го слоя?

Ответ: k(k – 1)(k – 2)·Ч ...·Ч 2 Ч 1. Это число называют “k факториал” и кратко обозначают k!.

Рис. 4

Для того чтобы решить эту задачу, достаточно “закодировать” любой такой путь последовательностью k различных чисел, нумерующих направления составляющих этот путь ребер.

В частности, число возрастающих путей от нулевой вершины до единичной равно n!. На любом таком пути есть единственная вершина, принадлежащая k-му слою, и она разбивает его на две части. Нижняя часть соединяет ее с нулевой вершиной, и этот путь — один из множества возможных путей, соединяющих ее с нулевой вершиной, которых, как мы уже знаем, ровно k!. Верхняя часть соединяет ее с единичной вершиной, и этот путь — один из множества возможных, которых, как легко понять по аналогии, в точности (n – k)!.

Рис. 5

Поэтому множество всех возрастающих путей от нулевой вершины до единичной, проходящих при этом через заданную вершину k-го слоя, равно k!(n – k)!. Но всего возрастающих путей от нулевой вершины до единичной n!, поэтому число вершин в k-м слое равно . Это число называется k-м биномиальным коэффициентом и обозначается кратко . Далее оно нам понадобится.

На этом мы заканчиваем рассказ о n-мерном кубе и возвращаемся в заключение опять к коду Грея. Очевидно, что в нем несоседние вершины могут быть соседними на кубе, т.е. соединяться в нем ребром. В некоторых приложениях, как теоретических, так и практических, представляет интерес построение цепи или цикла в n-мерном кубе, в которой несоседние вершины никогда не являются соседними в этом кубе. Такая цепь максимальной возможной длины называется “змеей в ящике”. Какова ее длина, до сих пор неизвестно. Наилучшие известные ее оценки принадлежат новосибирским математикам А.А. Евдокимову и А.Д. Коршунову.

Другой задачей, связанной с кодом Грея, но более простой, является его недвоичное обобщение. Например, как построить циклическую последовательность всех трехзначных десятичных чисел от 000 до 999, в которой каждые два соседних числа были бы соседними еще и в том смысле, что отличались бы ровно в одном разряде и ровно на единицу? Несколько проще построить такую последовательность, если считать цифры 0 и 9 также соседними, хотя разность между ними и не равна 1. Еще проще построить нециклическую последовательность с теми же свойствами.

Эта задача имеет приложение к алгоритму быстрейшего вскрытия кодового замка на дипломате, поэтому мы не приводим ее решения.

Заметим, что этим методом можно вскрыть, конечно, дипломат не только с десятичным, но и с любым k-ичным кодовым замком. Однако при нечетном k аналога циклического кода Грея не существует, а существует только “цепной” код Грея. Читателю предоставляется возможность самому это проверить.

§ 7. “Книга перемен”, азбука Морзе, шрифт Брайля и алфавитные коды

Двоичная система, по крайней мере в своей комбинаторной ипостаси, по существу была известна в Древнем Китае. В классической книге “И цзин” (“Книга перемен”) приведены так называемые “гексаграммы Фу-си”, первая из которых имеет вид , а последняя (64-я) — вид , причем они расположены по кругу и занумерованы в точном соответствии с двоичной системой (нулям и единицам соответствуют сплошные и прерывистые линии). Китайцы не поленились придумать для этих диаграмм специальные иероглифы и названия (например, первая из них называлась “кунь”, а последняя — “цянь”, сплошной линии сопоставляется мужское начало янь, а прерывистой линии — женское начало инь).

Каждая гексаграмма состоит из двух триграмм (верхней и нижней), им тоже соответствуют определенные иероглифы и названия. Например, триграмме из трех сплошных линий сопоставлен образ-атрибут “небо, творчество”, а триграмме из трех прерывистых линий сопоставлен образ-атрибут “земля, податливость, восприимчивость”. Их также принято располагать циклически, но этот цикл не является кодом Грея.

“Книга перемен” очень древняя, возможно, одна из древнейших в мире, и кто ее написал — неизвестно. Она использовалась ранее, и используется в настоящее время, в том числе и на Западе, для гадания. В Европе с аналогичной целью используются карты Таро. В чем-то обе эти системы схожи, но Таро никак не связаны с двоичной системой, поэтому о них мы говорить не будем.

Способ гадания по “Книге перемен” в кратком изложении таков. Бросается шесть раз монета (или лучше пуговица, деньги в гадании применять не рекомендуется), и по полученным результатам (орел или решка) разыскивается подходящая гексаграмма (для этого надо заранее сопоставить орлу и решке янь или инь). По гексаграмме разыскиваете соответствующий раздел “Книги перемен” (имеется перевод выдающегося синолога Ю.К. Шуцкого, неоднократно переиздававшийся в последнее время) и читаете, что там написано.

Конечно, перевод текста книги в предсказание требует опыта и мастерства. И заниматься этим надо после соответствующей подготовки, в подходящем настроении, в подходящее время и в подходящем месте. Говорят, тогда предсказания почти всегда сбываются. А может быть, просто магическим образом из множества вариантов будущего выбирается тот, который соответствует предсказанию?

Заинтересованного читателя отсылаем к книгам Дж.Х. Бреннана. Таинственный И цзин. М.: Гранд, 2001; В.Фирсова. Книга перемен. Мистика и магия Древнего Китая. М.: Центрполиграф, 2002, и переходим к другой теме — азбуке для слепых.

На этом примере, в частности, хорошо видно, что многие на первый взгляд простые идеи рождались не сразу, и своим появлением обязаны усилиям многих людей. Идею использовать рельефные буквы для печатания книг для слепых первым предложил француз Валентен Ойи. Но выпущенные им книги успехом не пользовались, так как слепым трудно было на ощупь отличать сложные начертания букв друг от друга.

Капитан французской армии Шарль Барбье в 1819 году предложил печатать выпуклыми не буквы, а точки и тире (или просто продавливать их на бумаге) и ими уже записывать буквы. Эту систему он назвал “ночное письмо” и предлагал вовсе не для слепых, а для использования в военно-полевых условиях. С появлением электрических фонариков военное значение этого изобретения упало до нуля.

Слепой мальчик Луи Брайль познакомился с этой системой в 12 лет. Она ему понравилась тем, что позволяла не только читать, но и писать. В течение трех лет он ее усовершенствовал и создал так называемый “шрифт Брайля”. В нем символы языка (буквы, знаки препинания и цифры) кодируются комбинациями от одной до шести выпуклых точек, расположенных в виде таблицы стандартного размера с тремя строчками и двумя столбцами. Элементы (точки) таблицы нумеруются числами 1, 2, 3 в первом столбце сверху вниз и 4, 5, 6 во втором столбце сверху вниз. Каждая точка либо продавливается специальной машинкой (или даже шилом), либо остается целой. Всего различных способов продавить выпуклые точки в этой таблице 64 (в том числе и тот, в котором ни одна из точек не вдавлена). При желании теперь читатель может сопоставить каждому символу алфавита Брайля одну из гексаграмм “Книги перемен”. Вряд ли, конечно, Брайль знал об этой книге.

Вероятно, не имеет смысла описывать все символы шрифта Брайля, тем более что после его смерти в 1852 году шрифт дополнялся и совершенствовался. Но несколько слов сказать, видимо, стоит. Буква “а”, например, изображается одной выпуклой точкой в 1-м элементе таблицы, буква “б” изображается выпуклыми точками в 1-м и 2-м элементах таблицы и т.д. Для сокращения текстов некоторые часто встречающиеся слова или комбинации букв кодируются специальными таблицами. Для того чтобы отличать заглавную букву от строчной, перед ней ставят специальную таблицу, изображающую то, что сейчас называют эскейп-символом. Многие таблицы имеют несколько значений (например, буква и какой-нибудь специальный знак или знак препинания), выбор из которых делается в соответствии с контекстом. Цифры кодируются так же, как и первые буквы алфавита, и, чтобы их отличать, перед последовательностью цифр ставится специальный символ — признак числа, а заканчивается число символом отмены признака числа.

Азбука Брайля по известности уступает азбуке Морзе, хотя и применяется до сих пор в отличие от последней. Сэмюэль Морзе известен, однако, не только изобретением азбуки. Он был и художником-портретистом (его картина “Генерал Лафайет” до сих пор висит в нью-йоркском Сити-Холле⁸), и одним из первых фотографов в Америке (учился делать дагерротипные фотографии у самого Луи Дагерра), и политиком (он баллотировался в 1836 году на пост мэра Нью-Йорка), но самое главное его достижение — изобретение телеграфа (а азбука Морзе понадобилась ему для использования телеграфа). Заодно он изобрел устройство, которое называется реле. Именно из реле спустя сто лет после Морзе были построены первые компьютеры.

Начал свои работы в этом направлении он в 1832 году, запатентовал свое изобретение в 1836 году, но публичная демонстрация телеграфа произошла только 24 мая 1844 года. По телеграфной линии, соединяющей Вашингтон с Балтимором, была успешно передана фраза из Библии.

Точки и тире оказались самыми элементарными символами, которые мог передавать его телеграф. Они соответствовали коротким и длинным импульсам электрического тока, передаваемым по телеграфным проводам. Длина импульса определялась нажатием руки телеграфиста на ключ телеграфа. Прием сигнала осуществляло реле, которое после появления в нем импульса тока включало электромагнит, который либо заставлял стучать молоточек, либо прижимал колесико с красящей лентой к бумажной ленте, на которой отпечатывалась либо точка, либо тире в зависимости от длины импульса.

Азбука Морзе сопоставляет каждой букве алфавита последовательность из точек и тире. Естественней всего использовать такие последовательности длины 6, их всего 64 и хватит даже на русский алфавит. Но Морзе понимал, что длину сообщения желательно уменьшить, насколько возможно, поэтому он решил использовать последовательности длины не более 4, их всего 2 + 4 + 8 + 16 = 30. В русском алфавите пришлось не использовать буквы “э” и “ё” и отождествить мягкий и твердый знаки. Кроме того, наиболее часто используемым буквам он предложил давать самые короткие коды, чтобы уменьшить среднюю длину передаваемого сообщения. Эту идею в наше время используют с той же целью в алфавитном кодировании.

Здесь имеет смысл ввести терминологию теории кодирования. Определение алфавитного кодирования очень просто. Пусть, например, кодирующим алфавитом является двухбуквенный алфавит, например, состоящий из символов 0, 1. Схемой алфавитного кодирования называется отображение каждой буквы кодируемого алфавита в некоторое слово в кодирующем алфавите (называемое элементарным кодом), в рассматриваемом случае — последовательность нулей или единиц. Пользуясь этой схемой, можно закодировать любое слово в кодируемом алфавите, заменяя в нем каждую букву на соответствующий ей элементарный код, и превратить исходное слово в более длинное слово в кодирующем алфавите. Таким образом, и код Брайля, и азбука Морзе являются алфавитными кодами.

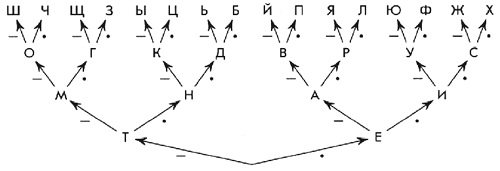
Удобнее всего задать код Морзе в виде четырехярусного двоичного дерева. Из корня дерева выходят два ребра, из которых правому соответствует тире, а левому — точка. Это — ребра первого яруса. Из их концов тоже аналогичным образом выходят по два ребра. Это — ребра второго яруса. Дерево рисуем до четвертого яруса. Вершинам дерева (за исключением корня) приписываем буквы алфавита (рис. 6). Тогда каждой букве можно сопоставить последовательность точек или тире, получающуюся, если выписать друг за другом последовательность символов, сопоставленных ребрам дерева, образующим путь, идущий из корня к вершине дерева, соответствующей данной букве.

Очевидно, что алфавитный код должен обладать свойством однозначной декодируемости, т.е. разные слова в исходном алфавите не могут иметь одинаковые коды. А так как процедуру декодирования можно представлять как поиск разбиения закодированного слова на элементарные коды, то это разделение должно быть однозначным. Поэтому однозначно декодируемые коды иногда называют разделимыми кодами. Ясно, что если все элементарные коды имеют одинаковую длину, то код разделим и алгоритм декодирования очень прост. Но если это не так, то код может и не быть разделимым. Например, таким является код Морзе. Но между словами телеграфисты всегда делали промежутки, поэтому никаких проблем не возникало. Однако если промежутки между словами выделять невозможно, приходится использовать только разделимые коды. А пустую букву, изображающую промежуток между словами, часто включают в состав алфавита, что дает возможность всегда иметь дело не с предложениями, а только со словами.

Понять по достаточно сложному алфавитному коду, является ли он разделимым, бывает не просто. Известны несколько разных алгоритмов для проверки разделимости кода. Наиболее наглядный из них принадлежит А.А. Маркову⁹.

Не вдаваясь в подробности, ограничимся замечанием, что код, у которого ни один из элементарных кодов не является началом другого (такие коды принято называть префиксными), несомненно, является разделимым. Предоставим доказательство этой теоремы читателю. Очевидным примером префиксного кода является любой код с равными длинами кодовых слов. Код Морзе префиксным не является, что также предоставляется проверить читателю. Любой двоичный префиксный код можно задать подобно коду Морзе с помощью двоичного дерева, не обязательно такого равномерного, как у него, но при этом буквы кодируемого алфавита должны сопоставляться только “листьям” дерева, но никак не внутренним вершинам.

Возвращаясь к истории алфавитного кодирования, заметим, что его корни уходят в глубь веков. Фактически первый пример применения алфавитного кодирования был описан древнегреческим историком Полибием. Алфавит записывался в квадратную таблицу 5 ґ 5, и каждая буква шифровалась парой своих координат       (i, j) (номерами строки и столбца), а передаваться сообщения могли в то время с помощью факелов — i факелов в левой руке и j факелов в правой означали пару      (i, j). Дальнейшее развитие идеи алфавитного кодирования принадлежит знаменитому английскому философу, эзотерику и писателю сэру Френсису Бэкону, который первым начал использовать двоичный алфавит в качестве шифроалфавита. В криптографии, правда, это не нашло особого применения, главным образом из-за пятикратного удлинения шифртекста в сравнении с открытым текстом. Но сам Бэкон предложил использовать его как метод, сочетающий криптографию со стеганографией (так называется скрытие самого факта передачи секретного сообщения).

Вместо двоичных цифр он использовал обычный алфавит, но со шрифтами двух типов. Таким методом можно было в любом тексте спрятать шифровку, если, конечно, шрифты были достаточно малоразличимы. Желательно при этом использовать разделимый код. Длина зашифрованного сообщения будет в несколько раз короче, чем длина содержащего его (и одновременно маскирующего его) текста, но если для передачи шифровки использовать книгу, то в ней можно таким образом незаметно разместить еще целую книгу. Но эта красивая идея из-за дороговизны ее реализации так и не нашла применения. В наше же время ее нельзя рассматривать как серьезный метод.

Интересно, что в XIX веке, главным образом в кругах, интересующихся наследием возникшего в средневековье тайного мистического ордена розенкрейцеров, появилась идея, что Френсис Бэкон, которого считали розенкрейцером, является настоящим автором пьес Шекспира. Начали искать подтверждение этого в шифрах, которые мог оставить Бэкон в своих книгах, а также в первом знаменитом издании пьес Шекспира. Было, естественно, найдено много таких, якобы зашифрованных фрагментов. Серьезные исследователи, правда, замечали, что в любом длинном тексте можно при желании и некоторых натяжках найти короткие фрагменты, напоминающие шифры. Но у сторонников авторства Бэкона стремление доказать это криптографическим методом приняло форму мании. Американский миллионер Фабиан даже создал в начале XX века на свои деньги лабораторию криптоанализа, которая занималась только подобными исследованиями.

Фабиан нанял на работу дипломированного генетика Уильяма Фридмана, сына эмигрантов из России. Через некоторое время Фридман уже возглавлял у Фабиана и лабораторию генетики, и лабораторию криптоанализа. Доказать авторство Бэкона он не смог, более того, он впоследствии опубликовал книгу, где опровергал возможность такого криптографического доказательства. Но он не на шутку увлекся криптографией и своей подчиненной Элизабет Смит, с которой обвенчался в 1917 году. Они стали самой знаменитой супружеской парой в истории криптографии. После вступления Америки в войну у него с супругой появилась серьезная работа по правительственным заказам. После войны он ушел от Фабиана и стал главным криптографом войск связи.

§ 8. Фотопленка и штрих-код

Рассмотрим теперь некоторые примеры реального применения двоичного кодирования в современной технике.

Как автоматические фотоаппараты узнают светочувствительность заправленной в них пленки? Ее измеряют в некоторых единицах, и вся выпускаемая сейчас в мире пленка имеет одно из 24 стандартных значений светочувствительности. Эти значения кодируются некоторым стандартным образом наборами из нулей и единиц, естественно, длины 5. На поверхности кассеты для пленки нанесены 12 квадратиков черного или серебристого цвета, образующих прямоугольник 2 ґ 6. Квадратики его верхней части мысленно занумеруем от 1 до 6, начиная слева. Квадратики нижней части аналогично занумеруем от 7 до 12. Серебристые квадратики — это просто металлическая поверхность кассеты, она проводит ток, который с контакта внутри аппарата подается на первый квадрат (он всегда серебристый). Черные квадраты покрыты краской, не проводящей ток.

Когда пленка вставляется в аппарат, шесть его контактов соприкасаются с шестью первыми квадратиками, и с квадратиков со 2-го по 6-й снимается информация — ноль, если квадратик черный и ток по соответствующему контакту не идет, и единица в противном случае. Вся информация о светочувствительности пленки заключена в квадратиках со 2-го по 6-й. В остальных квадратиках заключена информация о числе кадров в пленке и т.п.

Еще на поверхности кассеты можно увидеть штрих-код. Это так называемый “универсальный код продукта”, он сейчас ставится на всех продаваемых товарах. Для чего он нужен и как его прочитать?

Нужен он только для автоматического занесения информации в кассовый аппарат. Сам штрих-код состоит из тридцати черных полос переменной толщины, разделенной промежутками тоже переменной толщины. Толщина полос может принимать четыре значения — от самой тонкой до самой толстой. Такую же толщину могут иметь и промежутки. Когда по сканеру проводят штрих-кодом, он воспринимает каждую черную полоску как последовательность единиц длины от одной до четырех и также воспринимает промежутки между полосами, но при этом вместо единиц сканер видит нули. Полностью весь штрих-код сканер воспринимает как последовательность из 95 цифр 0 или 1 (их давно уже принято называть битами). Что же содержит этот код? Он кодирует 13-разрядное десятичное число, совершенно открыто написанное под самим штрих-кодом. Если сканер не смог распознать штрих-код, то это число кассир вводит в аппарат вручную. Штрих-код нужен лишь для облегчения распознавания сканером изображения. Распознавать цифры, к тому же повернутые боком, может только сложная программа распознавания на универсальном компьютере, да и то не очень надежно, а не кассовый аппарат.

Какую же информацию содержит это 13-значное число? Этот вопрос к математике никакого отношения не имеет. Первые две цифры задают страну — производителя товара. Следующие пять цифр — это код производителя, а следующие пять цифр — код самого продукта в принятой этим производителем кодировке. Последняя цифра — это код проверки. Он однозначно вычисляется по предыдущим 12 цифрам следующим образом. Нужно сложить все цифры с нечетными номерами, утроить сумму, к ней прибавить сумму оставшихся цифр, а полученный результат вычесть из ближайшего (большего) кратного 10 числа.

А вот 95-битный код, соответствующий штрих-коду, более интересен. Он содержит в себе только указанное 12-значное число (контрольная цифра в самом штрих-коде не содержится), но с большой избыточностью. Первые три бита в нем, так же, как и последние, — это всегда 101. Они нужны только для того, чтобы сканер смог определить ширину полосы, соответствующей одному биту (ведь размеры штрих-кода на разных упаковках могут быть разными) и настроиться на распознавание. В центре кода всегда стоит комбинация 01010, а левая и правая части кода состоят каждая из шести блоков по семь битов и содержат информацию о левых шести и правых шести из данных 12 десятичных цифр. Центральная комбинация позволяет, в частности, отличать поддельные или плохо напечатанные коды.

Цифры 13-значного кода кодируются в левой и правой частях штрих-кода по-разному. В левой половине каждая цифра кодируется семеркой битов, начинающейся с 0 и заканчивающейся 1 согласно следующей таблице:

В правой половине каждая цифра кодируется семеркой битов, начинающейся с 1 и заканчивающейся 0 согласно таблице, которая получается из вышеприведенной, если в ней нули заменить на единицы и единицы на нули (это переход к дополнительному коду). Можно заметить, что каждый из кодов в таблице содержит нечетное число единиц и ровно две группы рядом стоящих единиц и ровно две группы рядом стоящих нулей. Это означает, что каждая цифра соответствует двум соседним полосам на штрих-коде. Но более важно то обстоятельство, что все десять кодов таблицы, будучи прочитанными не слева направо, а справа налево, будут отличаться от любого из кодов таблицы, прочитанного правильным образом. Очевидно, таблица для правой половины кода обладает теми же свойствами, только число единиц в каждом коде четное.

Такая избыточная (не четырехбитовая, а семибитовая) таблица кодов нужна для того, чтобы сканер мог правильно прочитать штрих-код и в случае, когда код направляют в него “вверх ногами”. Как сканер может отличать одно направление от другого? По четности или нечетности числа единиц в первом же прочитанном семибитовом блоке, идущем после комбинации 101. При правильном направлении оно будет нечетным, а при обратном направлении — четным. Перепутать же коды, прочитанные слева, и коды, прочитанные справа, согласно свойству таблицы, невозможно.

Если же в каком-то из семибитовых блоков нарушено правильное чередование нулей и единиц в первом и последнем битах или ему не соответствует четность числа единиц, то штрих-код признается поддельным или плохо пропечатанным.

Продолжение в следующем номере.

^* Печатается по тексту одноименной книги. Издательство МЦНМО, 2004.

Двумя чертами слева выделены тексты задач для самостоятельного решения.

⁵ Приблизительный западный аналог — это конец света, но на Востоке считают, что после этого рождается новый Брахма, и все циклически повторяется сначала: от золотого века до нашей Кали-Юги, которой и заканчивается цикл.

⁶ Граф — это произвольное множество вершин, некоторые из которых соединены ребрами.

⁷ В честь ирландского математика, механика, физика и астронома У.Р. Гамильтона, подсказавшего одному книготорговцу идею головоломки — как обойти по ребрам все вершины правильного многогранника (например, додекаэдра) и вернуться в исходную вершину. Полученные от книготорговца десять фунтов были, вероятно, единственным гонораром знаменитого ученого за многочисленные научные труды, если не считать оклада профессора Дублинского университета.

⁸ Известна также его картина “Человек в предсмертной агонии”, после просмотра которой его приятель, известный врач, сказал: “По-моему, малярия”.