СЕМИНАР
С.Б. Гашков,
Москва
Системы счисления и их применения*
Продолжение. Начало в № 2, 3/2006.
§ 9. Задачи о переливаниях
На одной из Всесоюзных математических
олимпиад была предложена следующая задача. В три
сосуда налито по целому числу литров воды. В
любой сосуд разрешается перелить из любого
другого сосуда столько воды, сколько в нем уже
содержится. Каждый из сосудов может вместить всю
имеющуюся в них воду. Докажите, что можно
несколькими переливаниями освободить один из
сосудов.
В ее решении неожиданно на первый
взгляд применяется двоичная система. Так как
задача оказалась очень трудной (на олимпиаде ее
никто не решил), мы приведем здесь это решение. В
нем используются две идеи. Первая из них
заключается в том, что если будет найден алгоритм
переливания, после применения которого
минимальный объем воды, содержащейся в одном из
сосудов, уменьшается, то, повторяя многократно
этот алгоритм, мы опорожним один из сосудов. Эта
идея не такая простая, как может показаться. Ведь
это не что иное, как метод бесконечного спуска
П.Ферма.
Идея применения двоичной системы
лежит в основе этого алгоритма уменьшения
минимума. Пусть в сосудах A, B, C
находится a 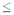 b b
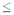 c литров воды.
Разделим b на a с остатком, b = aq + r,
0 c литров воды.
Разделим b на a с остатком, b = aq + r,
0 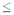 r < a и
предложим алгоритм, после применения которого в
сосуде B останется r литров. Для этого
представим q в виде суммы различных степеней
двойки: q = 2d1 + ... ... + 2dk . Выливая из
сосуда C воду d1 раз подряд в сосуд A,
получим в нем 2d1 a литров, а выливая
после этого в него 2d1 a литров из сосуда B,
получаем в нем b – 2d1a = a(q – 2d1)
+ r = a(2d2 + ... + 2dk) + r литров.
Аналогично, выливая из сосуда C воду d2
– d1 – 1 раз подряд в сосуд A, а потом
выливая в него воду из сосуда B, получаем в нем
a(2d2 + ... + 2dk) + r < a и
предложим алгоритм, после применения которого в
сосуде B останется r литров. Для этого
представим q в виде суммы различных степеней
двойки: q = 2d1 + ... ... + 2dk . Выливая из
сосуда C воду d1 раз подряд в сосуд A,
получим в нем 2d1 a литров, а выливая
после этого в него 2d1 a литров из сосуда B,
получаем в нем b – 2d1a = a(q – 2d1)
+ r = a(2d2 + ... + 2dk) + r литров.
Аналогично, выливая из сосуда C воду d2
– d1 – 1 раз подряд в сосуд A, а потом
выливая в него воду из сосуда B, получаем в нем
a(2d2 + ... + 2dk) +
+ r –2d2a = a(2d3 + ... + 2dk) + r
литров. Повторяя эту процедуру, получим, что в
конце концов в сосуде B окажется r литров
воды.
Нужно еще заметить, что во время каждой
процедуры из сосуда C выливалось меньше воды,
чем из сосуда B, так как 2 + 22 + ... + 2l-1
< 2l. Поэтому всего из сосуда C вылито
воды меньше, чем из B, значит, оба они не
опорожнятся раньше времени, и алгоритм работает
корректно.
Приведенную выше задачу можно
обобщить и на большее количество сосудов.
Применив к любым трем из них указанный алгоритм,
один из сосудов опорожним. Повторяя эту
процедуру еще раз, опорожним еще один сосуд и т.д.,
пока не останутся заполненными только два
сосуда.
Предоставляем читателю
самостоятельно выяснить, что будет происходить,
если продолжить переливания с двумя оставшимися
сосудами.
Выше указывалось, что при решении
некоторых задач о переливаниях можно
использовать аддитивные цепочки. Предлагаем
читателю для самостоятельного решения одну из
таких задач.
11. Как быстрее всего наполнить
флягу 85 литрами молока, пользуясь однолитровым
черпаком, если есть еще одна такая же фляга и
весы, способные только сравнивать массы фляг?
Классические задачи о переливаниях
выглядят несколько по-другому, и метод их решения
не связан с двоичной системой.
Примером такой задачи, решение которой
по преданию послужило знаменитому французскому
математику Пуассону толчком к выбору его
профессии, является вопрос о том, как, имея полные
сосуды в 3 и 5 литров и пустой 8-литровый сосуд,
отмерить ровно 4 литра. Читателю предоставляется
возможность самостоятельно придумать метод
решения подобных задач за наименьшее количество
переливаний.
§ 10. Игра “Ним”
Двоичная система находит неожиданное
применение при анализе известной игры “Ним”.
Происхождение ее, так же, как и шахмат, покрыто
туманом. Возможно, она была изобретена в Китае.
Состоит она в следующем: на столе лежит
несколько кучек спичек, и два игрока по очереди
выбирают одну из кучек и забирают из нее сколько
угодно спичек (хоть все); выигрывает тот, кто
забирает последнюю (есть вариант игры, в котором
забравший последнюю проигрывает). Эпизод с этой
игрой неоднократно повторяется в известном
французском фильме “Прошлым летом в
Мариенбаде”.
Игра “Ним” являлась излюбленной
темой математических кружков в МГУ. Иногда она
представлялась в виде гонки нескольких пешек от
одного края доски до другого. Читатель сам сможет
сформулировать правила игры в таком ее
представлении.
При игре с одной кучкой, очевидно,
побеждает начинающий.
При игре с двумя кучками начинающий
побеждает не всегда.
12. Докажите, что выигрывающей
позицией является позиция с двумя равными
кучками. Игрок, сумевший после своего хода
попасть в такую позицию, всегда сможет выиграть.
В случае трех и более кучек описание
выигрышной позиции не так просто. Алгоритм
распознавания выигрышной позиции следующий.
Нужно количество спичек в каждой кучке записать
в двоичной системе и вычислить сумму по модулю 2
полученных двоичных наборов (далее для краткости
будем называть ее ним-суммой).
Для этого вначале нужно вычислить
покомпонентную сумму этих наборов, т.е. найти
сумму всех младших разрядов, потом сумму
следующих за ними разрядов (отсутствующие
разряды заменяются нулями)
и т.д., и записать полученные суммы в виде
(возможно, недвоичного) набора, а потом каждую его
компоненту заменить на остаток от деления на 2.
Если получится набор из одних нулей, то позиция
выигрышная.
Например, если в кучках было 3, 7, 12, 17
спичек, то покомпонентно складывать придется
наборы
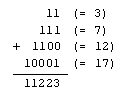
Ним-сумма равна 11001, поэтому позиция
является проигрышной для того, кто в нее попал
после своего хода. Причина в том, что противник
может сделать ход, которым он попадет в позицию с
нулевой ним-суммой. Для этого он может оставить в
последней кучке число спичек, равное в двоичной
записи ним-суммы наборов 10001 и 11001, т.е. 01000. Тогда
ним-сумма чисел, образующих новую позицию, будет
равна нулевому набору, так как эта сумма будет
отличаться от прежней суммы 11001 прибавлением к
ней по модулю 2 набора 11001, что дает в результате,
очевидно, нулевой набор. Поскольку 01000 = 8, из
последней кучки надо взять 17 – 8 = 9 спичек.
13. Докажите в общем случае, что из
позиции с ненулевой ним-суммой за один ход можно
попасть в позицию с нулевой ним-суммой, а из
позиции с нулевой ним-суммой любой ход ведет к
позиции с ненулевой ним-суммой.
Теперь ясно, что тот, кто первый попал в
позицию с нулевой ним-суммой, дальше при любой
игре противника при своем ходе опять сможет
попасть в такую же позицию, и в конце концов он
возьмет последнюю спичку.
Указанная выигрышная стратегия
поддается для реализации даже на
специализированных машинах. Одна из таких машин
была выставлена после войны в Берлине на
английской выставке и с успехом конкурировала с
находящимся рядом бесплатным пивным залом.
Знаменитый английский математик Алан
Тьюринг вспоминал о том, как популярность этой
машины повысилась еще больше после победы над
тогдашним бундесминистром экономики Л.Эрхардом.
Читателю предоставляем возможность
найти выигрышную стратегию при игре “Ним” в
поддавки.
Более интересная модификация игры
“Ним” получается, если ограничить число спичек,
которые можно взять за один раз, например, числом
10. Тогда интерес представляет даже игра с одной
кучкой спичек. Эту игру изобрел в XVII веке
французский математик Баше де Мезириак,
написавший, кстати, одну из первых в Европе книг
по занимательной математике. Читатель может
попробовать сам придумать для нее выигрышную
стратегию.
§ 11. Д.И. Менделеев и троичная система
Когда мы рассматривали задачу о
взвешивании с помощью гирь, мы предположили, что
груз лежит на одной чашке, а гири — на другой. Но
если разрешить класть гири на обе чашки весов, то
ответ в задаче об оптимальной системе разновесок
изменится. Оптимальной теперь будет система из
гирек с массами, образованными степенями тройки.
Этой задачей интересовался Д.И. Менделеев в
бытность свою председателем Российской палаты
мер и весов10.
Оказалось, что частный случай этой
задачи был опубликован в книге Баше де Мезириака
в XVII веке, а ранее был известен Фибоначчи.
Спрашивалось, какое наименьшее число гирь нужно
иметь, чтобы можно было взвесить любой груз от 1
до 40 г. Оптимальным оказался набор гирь 1, 3, 9, 27 г.
Для того чтобы взвесить груз в n г, надо
представить число n в виде суммы a0 + 3a1
+ 9a2 + 27a3, где ai = 0,
±1 (i = 0, 1, 2, 3). Тогда для его взвешивания
достаточно на чашку вместе с грузом положить все
гири, массы которых входят в эту сумму со знаком
минус, а на противоположную чашку положить все
гири, массы которых входят в эту сумму со знаком
плюс.
Но как найти такую сумму? Один из
возможных способов решения этой задачи основан
на сведении ее к представлению числа n + 40 в
виде суммы
b0 + 3b1 + 9b2 + 27b3,
где bi = 0, 1, 2 (i = 0, 1, 2, 3). Мы уже
знаем, что эта задача равносильна представлению
числа n + 40 в троичной системе n + 40 = (b0b1b2b3)3.
Один из алгоритмов ее решения заключается в том,
что на правую чашку весов кладутся вначале самые
тяжелые гири, потом гири меньшего веса и т.д.
Например, этот алгоритм для числа 40 дает
разложение 40 = 27 + 9 + 3 + 1. Если мы уравновесили
массу n + 40 г, положив на чашку bi гирь массы
3i (i = 0, 1, 2, 3), то, перекладывая на
другую чашку по одной гире каждой массы, мы
уравновесим n г. На алгебраическом языке это
означает, что будет получено равенство n = a0
+ 3a1 + 9a2 + 27a3, ai
= bi – 1 (i = 0, 1, 2, 3). Очевидно, что
при этом ai = 0, ±1 (i = 0, 1, 2, 3). Верно
и обратное, а именно, из разложения n = a0
+ 3a1 + 9a2 + 27a3, ai
= 0, ±1 (i = 0, 1, 2, 3) можно получить разложение n
+ 40 = b0 + 3b1 + 9b2 + 27b3,
bi = 0, 1, 2
(i = 0, 1, 2, 3). Поэтому из известной нам
единственности представления n + 40 = b0
+ 3b1 + 9b2 + 27b3, bi
= 0, 1, 2 (i = 0, 1, 2, 3), означающей единственность
записи данного числа в троичной системе,
вытекает единственность представления
n = a0 + 3a1 + 9a2 + 27a3,
ai = 0, ±1 (i = 0, 1, 2, 3), означающая
единственность записи данного числа в так
называемой уравновешенной троичной системе, n
= (a0a1a2a3)3.
Эта система способна составить
некоторую конкуренцию двоичной системе как по
простоте арифметических алгоритмов, так и по
количеству применений в математических задачах.
Удобным ее свойством является то, что для
изменения знака у представляемого числа
достаточно изменить знаки у всех его цифр.
В общем виде доказанные выше
утверждения можно записать следующим образом.
Любое целое число от –(3n – 1)/2
до (3n – 1)/2 может быть однозначно
представлено в виде 3n – 1bn-1 +
... + 3b1 + b0, где bi =
0, ±1. Для того чтобы взвесить любой груз от 1 до (3n–1)/2
г за одно взвешивание, достаточно иметь гири 1, 3, 9,
..., 3n–1 г.
Читатель легко докажет все это
самостоятельно, если заметит, что (3n –
1)/2 = 1 + 3 + 32 + ... + 3n–1, другими словами,
троичная запись числа (3n – 1)/2 состоит
из одних единиц.
Докажем, что меньшего количества гирь
недостаточно, и предложенная система для грузов
от 1 до (3n – 1)/2 г оптимальна. Допустим,
что есть система из n – 1 гирь с массами g1,
..., gn-1, позволяющая взвесить любой из
этих грузов. Это значит, что любое число m от
–(3n – 1)/2 до (3n – 1)/2 можно
представить в виде алгебраической суммы a1g1
+ ... + an-1gn-1, ai = 0,
±1, (i = 1, ..., n – 1). Но таких сумм ровно 3n–1,
так как каждое слагаемое входит в нее с одним из
трех возможных коэффициентов. Но 3n–1
меньше общего числа различных грузов, равного 3n.
14. Покажите, что оптимальная
система гирь для взвешивания грузов от 1 до (3n
– 1)/2 определена однозначно.
15. Докажите, что для взвешивания
любого груза от 1 до m г, (3n–1 – 1)/2 < m
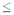 (3n – 1)/2,
наименьшее количество гирь равно n, а в случае
m < (3n – 1)/2 выбор гирь неоднозначен. (3n – 1)/2,
наименьшее количество гирь равно n, а в случае
m < (3n – 1)/2 выбор гирь неоднозначен.
Уравновешенная троичная система,
кроме указанного выше свойства, обладает еще
несколькими удобными свойствами. Например, для
выполнения округления в этой системе достаточно
просто отбросить лишние цифры. В
неуравновешенной системе, даже двоичной,
округление выполняется не так просто. Так же
просто, как и в уравновешенной системе,
производится сравнение чисел по величине, но не
нужно обращать при этом внимание на знак числа.
Кстати, знак числа в этой системе
определяется знаком старшей ненулевой цифры, и
не нужно использовать специальный знаковый бит,
как в двоичной системе. А таблицы сложения,
умножения и деления почти так же просты, как и в
двоичной системе.
Вычитание же просто сводится к
сложению со сменой знака у вычитаемого. При
записи чисел в этой системе удобно вместо –1
писать . Так как таблица умножения и деления
совсем просты, приведем только таблицу сложения:
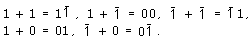
Умножение, как и деление, тоже сводится
к перемене знака и сложению. Другим достоинством
троичной системы является то, что запись в ней
имеет длину на одну треть меньше, чем в двоичной.
Видимо, благодаря им троичная
уравновешенная система была положена в основу
советского компьютера “Сетунь”, построенного в
конце 1950-х годов.
Однако широкого распространения она
не получила, так как все же элементная база
компьютеров, как того времени, так и современных,
остается двоичной, а битовое представление
троичной системы даже длиннее, чем двоичной.
Уравновешенная система может быть
рассмотрена и для любого натурального основания,
правда, при четном основании запись в ней
перестает быть однозначной. Преимуществом
уравновешенных систем является то, что в них
записываются и отрицательные числа без знака
минус перед записью, а также то, что таблица
умножения в этих системах в сравнении с обычными
примерно в четыре раза короче, как отметил О.Л.
Коши.
16. Запишите число (1 234 567 890)10 в
уравновешенной десятичной системе счисления.
Утверждение следующей задачи на
первый взгляд кажется ложным, однако
присмотритесь к ней повнимательнее.
17. Докажите, что любое ненулевое
целое число имеет единственное знакопеременное
двоичное представление – 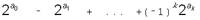 , где a0 < a1 < ... < ak. , где a0 < a1 < ... < ak.
Десятичную запись чисел можно
преобразовать в запись, состоящую из цифр 0, ±1, ±2,
±3, ±4, ±5, заменяя все цифры, большие 5, на их
дополнения до 10, взятые с противоположным знаком,
и делая при этом единичный перенос в следующий
разряд. Сложение и умножение таких записей можно
делать так же, как и обычных, только при этом
переносы в следующие разряды могут быть
отрицательными. Оценки для числа операций при
этом не улучшатся, но сами операции в некотором
смысле станут проще, так как для их выполнения
достаточно помнить таблицу умножения 5 ґ 5.
Например, перемножим числа 89 и 98. Запишем первое
из них как (1 –1 –1), а второе — (1 0 –2). Умножаем
столбиком:
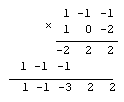
К счастью, не пришлось делать
переносов, но это не труднее, чем в обычном
умножении (заметим, что при умножении обычных
записей этих чисел переносы чуть ли не в каждом
разряде).
Осталось перевести ответ в обычную
запись:
(1 –1 –3 2 2) = 8722.
§ 12. Троичная система и фокус
Жергонна
Троичная система удачно применяется
при объяснении следующего фокуса Жергонна
(французского математика XIX века).
Зритель запоминает одну из 27 карт и
выкладывает их в три стопки по девять карт
картинками вверх (первая карта идет в первую
стопку, вторая — во вторую, третья — в третью,
четвертая — в первую и т.д.). Фокуснику
сообщается, в какой из стопок задуманная карта,
потом стопки складываются в любом из шести
возможных порядков (не перетасовывая карты
внутри стопок) и раскладываются снова в три
стопки, начиная с верхней карты, потом
складываются опять и процедура повторяется в
третий раз (каждый раз сообщается, в какую из
стопок легла запомненная карта). Фокусник каждый
раз замечает, куда легла стопка с запомненной
картой — в верх (фокусник запоминает символ 0), в
середину (символ 1) или в низ колоды (символ 2), и
составляет из этих символов трехзначное число в
троичной системе счисления, ставя первый из
замеченных символов в младший разряд, следующий
символ — во второй и последний символ — в
старший разряд.
К полученному числу прибавляется
единица и отсчитывается такое количество карт,
начиная с верхней карты колоды, — последняя из
отсчитанных карт и есть запомненная зрителем.
18. Объясните фокус Жергонна.
Имеется еще один вариант фокуса
Жергонна, но с другим способом раскладки карт.
Колода из 27 карт раскладывается на три стопки в
следующем порядке: первая карта — в первую
стопку, вторая — во вторую, третья — в третью,
четвертая — опять в третью, пятая — во вторую,
шестая — в первую и т.д. Одна из карт запоминается
зрителем, и указывается стопка, в которой она
лежит, и все повторяется еще два раза. Способ
угадывания тот же самый. Можно показывать тот же
фокус и с 21 картой, но тогда надо раскладывать
карты самому и стопку с задуманной картой всегда
класть в середину колоды.
19. Докажите, что в фокусе с 21 картой
после трех перекладываний задуманная карта
окажется точно в середине колоды, т.е. на 11-м месте
от любого края.
Приведем еще одну задачу, при решении
которой может пригодиться троичная система.
20. Докажите, что среди чисел от 1 до 3n
– 1 можно найти 2n таких, что никакое
среди них не является средним арифметическим
двух других.
§ 13. Немного об истории позиционных систем
счисления
Еще средневековые математики Ближнего
Востока нашли простой подход к вычислениям с
дробными числами — использование десятичных
дробей. Десятичная система попала туда, видимо,
из Индии, хотя позиционные дроби, правда, не
десятичные, a шестидесятеричные, были известны
еще в Древнем Шумере, а десятичные дроби, по
существу, были известны в Древнем Китае. Индейцы
майя, вероятно, использовали двадцатеричную
систему.
Здесь уместно вспомнить, что запись (bn
... b0, b-1 ... b-k)b
в позиционной системе счисления с основанием b
означает число, равное bnbn + ... + b1b
+ b0 + b-1b–1 + ... + b-kb–k,
где bnbn +...+ b1b + b0
— его целая, а b-1b–1 + ... + b-kb–k
— дробная часть.
В западных странах вместо запятой, отделяющей
целую часть от дробной, используется точка.
Почему обычно используется десятичная
система? Главным образом, в силу традиции
(которая, вероятно, основывается на том, что число
пальцев на обеих руках равно обычно 10; индейцы
майя, возможно, не забыли и про ноги). Как писал
Паскаль, десятичная система ничем не лучше
систем с другими основаниями. С некоторых точек
зрения более удобны другие системы. Так, много
поклонников имеет двенадцатеричная система
(идущая от счета дюжинами и гроссами — дюжинами
дюжин). Возможно, к их числу относился и Г. Дж.
Уэллс (см. его роман “Когда спящий проснется”).
Преимущество этой системы в том, что 12 имеет
больше делителей, чем 10, что несколько упрощает
деление.
С этой точки зрения еще лучше шестидесятеричная
система (но таблица умножения в этой системе
вгоняет в дрожь). Остатки от былого
распространения этой системы видны в
картографии и астрономии, а алгоритм перевода из
этой системы в десятичную запаян в любом
калькуляторе для научных расчетов (речь идет о
переводе из градусной меры в десятичную и
обратно). Кстати, первая запись дробного числа в
позиционной системе в Европе была сделана в XIII
веке Фибоначчи: корень уравнения
x3 + 2x2 + 10x = 20 он нашел в виде
1° 26' 7'' 42'''.
Есть поклонники и у восьмеричной и
шестнадцатеричной систем. Первую из них хотел
ввести в Швеции Карл ХII (который, возможно, пришел
к этой идее самостоятельно), но ряд обстоятельств
помешали этому прогрессивному начинанию (среди
них, вероятно, и занятость короля в военных
кампаниях, в частности, в России). Преимущество
этих систем в том, что легко осуществляется
перевод в двоичную систему и обратно.
Основатель теории множеств уроженец
Петербурга Георг Кантор предложил рассматривать
системы счисления со смешанными основаниями.
Запись в таких системах выглядит так:
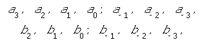
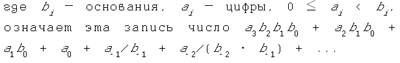
Частным случаем таких систем
является факториальная, которая получается при bk
= k + 2, b-k = k + 1. Используя ее,
можно любое натуральное число представить в виде
ann! + ... + a22! + a11!, где 0 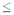 ak ak 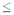 k. k.
Системы со смешанными основаниями
всем известны из повседневной жизни. Например, “1
неделя 2 дня 3 часа 4 минуты 56 секунд 789
миллисекунд” равно
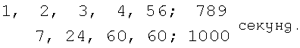
§ 14. Cхема Горнера и перевод из одной
позиционной системы в другую
Использованный в бинарном методе (см. §
2) прием вычисления числа по его двоичной записи
является примером более общего алгоритма,
называемого схемой Горнера. Схема Горнера —
это алгоритм для вычисления частного и остатка
от деления многочлена p(x) на х – a.
Кратко опишем, как он устроен и как связан с
переводом числа из одной системы в другую.
Пусть дан произвольный многочлен
p(x) = unxn + ... + u1x
+ u0.
Деление этого многочлена на x – a
— это представление его в виде p(x) = (x –
a)h(x) + r, h(x) = vn-1xn–1
+ ... + v1x + v0. Непосредственно
можно проверить, что коэффициенты частного можно
найти по формулам vn-1 = un, vn-2
= un-1 +avn-1, ..., v0 = u1
+ av1, а остаток можно вычислить по
формулам r = u0 + av0 = u0
+ a(u1 + av1) = u0 + a(u1+
a(u2 + av2)) = ... = u0 + a(u1
+ a(...(un-1 + aun)...) = unan
+ ... + u1a + u0 = p(a).
Этот метод вычисления и называется
схемой Горнера. Слово “схема” в названии
алгоритма связано с тем, что обычно его
выполнение оформляют следующим образом. Сначала
рисуют таблицу 2 x (n + 2). В левой нижней клетке
записывают число a, а в верхней строке —
коэффициенты un, un-1, ..., u0
многочлена p(x), при этом левую верхнюю
клетку оставляют пустой:

После этого под числом un
записывают un. Далее на каждом шаге последнее
записанное число умножают на a, к результату
прибавляют число, стоящее справа сверху от
последнего записанного числа, и полученную сумму
записывают в клетку справа от этого числа:
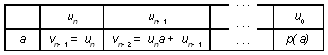
Число, которое после выполнения
алгоритма оказывается записанным в правой
нижней клетке, и есть остаток p(a) деления
многочлена p(x) на x – a. Другие
числа vn–1, vn–2, ... нижней
строки являются коэффициентами частного.
Например, деление многочлена p(x)
= x3 – 2x + 3 на x – 2 по описанному
алгоритму выполняется так:
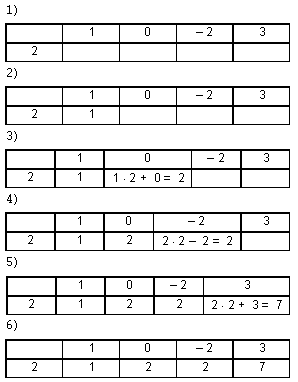
Получаем, что
x3 – 2x + 3 = (x – 2)(x2
+ 2x + 2) + 7.
Общее число операций, используемых в
этом алгоритме, равно n плюс число ненулевых
коэффициентов у многочлена p(x) минус
единица.
Схема Горнера была на самом деле
применена англичанином Горнером (а еще раньше
итальянцем Руффини) для вычисления
коэффициентов многочлена p(x + c) и
использовалась для приближенного вычисления
корней многочленов11. Мы укажем некоторые
другие ее применения. Одно из них — быстрый
алгоритм перевода из двоичной системы в
десятичную, предложенный Соденом в 1953 году.
Сначала переведем число из двоичной
системы в восьмеричную. Для этого разбиваем
справа налево его цифры на “тройки” (последняя
“тройка” на самом деле может быть “двойкой”
или даже одной цифрой) и переводим их в
восьмеричную систему схемой Горнера
(выполняемой устно). Например,
(1111110000)2 = (1.111.110.000)2 = (1760)8.
Выполним перевод из восьмеричной
системы в десятичную.
Пусть u = (un ... u1)8.
На k-м шаге выполняем над полученной на
предыдущем шаге записью в десятичной арифметике
действия:
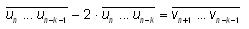
и получаем запись 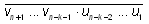 (старшие разряды могут оказаться
нулевыми и в реальных вычислениях участвовать не
будут). На (n–1)-м шаге получаем десятичную
запись числа u. (старшие разряды могут оказаться
нулевыми и в реальных вычислениях участвовать не
будут). На (n–1)-м шаге получаем десятичную
запись числа u.
Например,
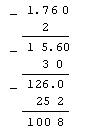
Алгоритм перевода из десятичной
системы в двоичную, предложенный Розье в 1962 году,
почти такой же. Сначала переводим в восьмеричную
запись. Для этого, пользуясь восьмеричной
арифметикой, на k-м шаге выполняем над
полученной на предыдущем шаге записью действия:
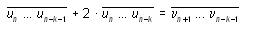
и получаем запись 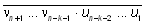 (поначалу (n+1)-е разряды
окажутся нулевыми и в реальных вычислениях
участвовать не будут). На (n–1)-м шаге получаем
восьмеричную запись числа u. Например, (поначалу (n+1)-е разряды
окажутся нулевыми и в реальных вычислениях
участвовать не будут). На (n–1)-м шаге получаем
восьмеричную запись числа u. Например,
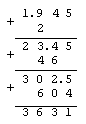
Далее переводим восьмеричное n-значное
число в двоичное (вычисляя для каждой
восьмеричной цифры двумя делениями на 2 с
остатком ее двоичную запись).
21. Переведите из десятичной
системы в двоичную систему число 12345678987654321.
22. Переведите из двоичной системы в
десятичную систему число 10101010101010101.
Продолжение следует
* Печатается по тексту
одноименной книги. Издательство МЦНМО, 2004.
Тексты задач для самостоятельного решения
углублены по тексту.
10 Менделеев имел широкие интересы как в
чистой, так и в прикладной науке. Он занимался,
например, и экономикой, и демографией, известны
его исследования об оптимальной концентрации
спирта в воде при производстве водки, по просьбе
генштаба он раскрыл состав артиллерийского
пороха, используемого немецкой армией. Отвечая
на один вопрос Менделеева, А.А. Марков написал
знаменитую работу об оценке производной
многочлена через величину его максимального
значения на отрезке.
11 Впрочем, лежащая в ее основе идея была
известна Ньютону и, может быть, даже до него.
|