ЖАРКОЕ ЛЕТО-2006Компьютерные модели в школьном курсе физикиР.В. Бирих, Е.А. Еремин, В.А. ЧернатынскийОт авторовВ связи с проведением реформы в сфере образования появляются новые виды учебных дисциплин, такие, как, например, профильные или курсы по выбору (так называемые “элективные”) и некоторые другие. Это не может не приводить к поискам глубоких по содержанию, но в то же время интересных для учеников и коротких учебных курсов. Авторы предлагают вашему вниманию один из вариантов подобного курса, сочетающего в себе мировоззренческие знания о фундаментальных законах природы с наглядной и современной формой компьютерного практикума.
Особенностью предлагаемых материалов является моделирование физических процессов на серьезном научном уровне (хотя и с учетом реальных знаний школьников). Усвоение материала в полной постановке дает возможность ученикам научиться современным методам теоретического исследования природных процессов. В последнее время появилось большое количество электронных учебных материалов по физике, например, на компакт-дисках или в виде сетевых ресурсов. Как правило, они либо не оставляют учащимся возможности для творческого внесения исправлений в имеющиеся там модели, либо такая деятельность требует от них освоения весьма специфических для данной среды приемов. Предлагаемый практикум опирается лишь на стандартный уровень работы с широко распространенными системами Delphi и Excel, освоение которых не только не является делом узкоспециальным, но, напротив, они широко применяются во многих других областях. С этой точки зрения практикум должен заинтересовать учителей информатики, тем более что они найдут в программной части примеры нетривиального решения некоторых проблем. Особо подчеркнем, что вполне возможен и упрощенный вариант реализации курса без всякого программирования: обратиться на сайт редакции в раздел Download, выбрать среди имеющихся там материалов готовые реализации приложений для моделирования, загрузить их, а затем сосредоточить свое внимание только на физических проблемах. Подобный подход, возможно, заинтересует учителей физики. Компьютерное обеспечение практикума можно получить на сайте “Информатики” в разделе “Download” 1. Модели и цели моделированияСлова “модель” и “моделирование” в последние годы стали часто использоваться и в учебной литературе, и в обычных жизненных ситуациях. Моделью называют девушку, которая демонстрирует новые покрои одежды, или, глядя на которую, художник рисует картину. Плюшевого медвежонка и другие разнообразные игрушки, с которыми имеет дело ребенок в повседневной жизни, современные учебники информатики также называют моделями. Линию, которую по линейке провел школьник в своей тетради, некоторые учителя склонны называть моделью прямой, желая подчеркнуть ее несовершенство и отличие от “настоящей” математической прямой. Моделью называют плоское графическое или объемное изображение будущего городского микрорайона. Многие считают произведения искусства и литературы моделью “человеческой души”. Систематизированные сведения, представленные об объекте в электронном виде, называемые раньше базой данных, теперь многие методисты считают целесообразным называть информационной моделью объекта. Достаточно распространенным является мнение о том, что совокупность наших знаний о природе образует ее модель [1, 2]. Словарь иностранных слов выделяет шесть разных смыслов слова “модель”: 1) образец какого-либо изделия для серийного производства; 2) тип, марка, образец конструкции чего-либо; 3) воспроизведение предмета в уменьшенном или увеличенном виде; 4) предмет изображения в искусстве, натурщица, позирующая художнику; 5) образец предмета, служащий для изготовления формы при воспроизведении в другом материале; 6) схема, изображение или описание какого-либо явления или процесса в природе и обществе. В слово “моделирование”, по своему грамматическому устройству означающему некоторое действие, вкладывается еще более широкий смысл. Это, во-первых, построение всякого рода моделей. Поскольку человек всегда действует по некоторому заранее подготовленному плану, поэтому считается, что результатом его деятельности является некоторая модель [1]. С этой точки зрения все, что сделано человеческими руками или при его вмешательстве, можно считать моделью. Следуя этому взгляду, например, дворник, убирая улицу после ночного снегопада, создает модель чистой улицы. Во-вторых, под моделированием понимают экспериментальное исследование свойств моделей и критическую оценку их возможностей. В-третьих, использование моделей для формирования умений и навыков. Обратим внимание еще на существование в “чистой” математике своей строгой теории моделей [3]. Ясно, что такое широкое понимание модели и моделирования, далекое от конструктивного, научного смысла этих слов, делает эти термины малосодержательными или требует классификации, которая из-за многообразия смысла исходных понятий не может быть однозначной и полезной. Широкая дискуссия о том, как в школьном курсе вести понятие модели: на основе строго философского определения [4] или интуитивного бытового понимания этого слова, — не может привести к однозначному решению. В связи с этой проблемой нам кажется интересной публикация [5]. Компьютерное моделирование предполагает использование универсального исполнителя — персонального компьютера. На наш взгляд, разумно не классифицировать виды компьютерных моделей, а говорить об области знаний или деятельности, в которых компьютерное моделирование осуществляется. Например, компьютерное моделирование в градостроении, компьютерное моделирование чрезвычайных ситуаций в природе, компьютерное моделирование высокомолекулярных соединений, компьютерное моделирование физических процессов. Как же ограничить понятие модели и моделирования для наших целей исследования физических процессов? Вот что говорит по этому поводу “Физический энциклопедический словарь” 1963 года издания [6], когда слово “модель” не было в такой моде: “Моделирование — метод экспериментального исследования, основанный на замещении конкретного объекта эксперимента (образца) другим, ему подобным (моделью). Моделирование применяется в тех случаях, когда целью исследования является не выяснение общих физических закономерностей, а детальное изучение вполне конкретного процесса, развивающегося в системе с определенными геометрическими и физическими свойствами при заданных режимных условиях”. Далее мы будем придерживаться такой точки зрения и более подробно обсудим эти идеи. Окружающий человека мир действительно сложен и разнообразен. В процессе его познания человек вынужден выделять в исследуемых объектах наиболее важные черты и свойства, а в происходящих явлениях существенные связи. Для определения количественных связей экспериментатор создает достаточно сложные приборы и установки. Они являются обычными физическими объектами, в которых конструктивно второстепенные связи отодвинуты на второй план, и это позволяет экспериментатору установить количественные закономерности. Важнейшие из них составляют содержание законов природы. Называть чувствительные установки экспериментатора моделями чего-либо вряд ли разумно. Например, известные крутильные весы Кулона, на которых измерялась сила взаимодействия заряженных шариков, являются моделью чего? В том случае, когда устанавливаются фундаментальные законы или изучаются физико-химические свойства тел, экспериментатор проводит, как говорят, натурные эксперименты (опыты Галилея, Кулона, Фарадея — этот список можно долго продолжать). Например, для установления закона всемирного тяготения нужно измерить силу притяжения двух тел, в качестве которых могут быть взяты астрономические тела или большие шары. Для формулировки закона Ома необходимо для разных проводников в эксперименте установить связь между током в цепи и напряжением на концах проводника. Для определения вязкости жидкости нужно эту жидкость залить в вискозиметр и провести измерение. Следует еще раз подчеркнуть, что для проведения некоторых экспериментов исследователям приходится делать очень сложные в техническом отношении установки (не модели). В физической науке, особенно на первоначальном этапе ее развития, доминировали натурные эксперименты. Они должны занимать определенное место и в процессе обучения физике как источник первоначального знания о законах природы. Иллюстрация физических законов, на наш взгляд, в случае возможности должна производиться в натурном эксперименте. Только в натурном эксперименте можно убедиться в справедливости того или иного закона! В кино и на экране компьютера можно показать все, что угодно! В современной науке, однако, ситуация несколько изменилась. Часто возникает потребность в эксперименте, в котором не требуется открывать фундаментальные законы природы, а необходимо установить поведение какого-либо конкретного объекта или характер протекания конкретного процесса в рамках известного класса явлений. Например, вы придумали новую форму корпуса самолета и хотите узнать его летные качества. Хотя физика происходящих в окрестности самолета явлений достаточно ясна, разумно ли сразу строить аппарат натуральных размеров и проводить полетные эксперименты? Или другой пример: в технологическом процессе подготовки высококачественной стали требуется ввести легирующую добавку. В какой момент времени и в каком месте это сделать, особенно если добавка может выгореть? Можно ли без больших затрат провести прямой эксперимент? Ответ на эти вопросы один: требуются предварительные эксперименты на вспомогательных объектах. Для детального изучения свойств конкретных объектов и сложных явлений современный исследователь создает вспомогательные объекты, с которыми ему легче экспериментировать, во взаимодействии которых удобней наблюдать интересующие явления. Как говорилось выше, метод экспериментального исследования, основанный на замене конкретного объекта эксперимента другим, в некотором смысле ему подобным, будем называть моделированием, а объект, над (на) которым (ом) производится эксперимент, — моделью. Именно только в этом смысле дальше будут употребляться слова “модель” и “моделирование”. Обычно модель предназначается для изучения вполне конкретного процесса, происходящего в системе с определенными геометрическими параметрами и физическими свойствами в условиях, когда обстановка для натурного эксперимента неблагоприятна. Например, геометрические размеры системы чрезмерно велики или очень малы, исследуемый процесс протекает слишком быстро или слишком медленно, очень высоки значения режимных параметров процесса (температура, давление, электрическое напряжение и т.п.), дороговизна или токсичность расходуемых материалов и другие факторы. Почему мы надеемся получить знание об объекте, экспериментируя на модели? Модель и моделируемый объект связывают условия подобия, что и позволяет на модели воспроизводить явления, подобные тем, которые происходят в объекте (об этом говорит опыт). Модель, конечно, должна быть геометрически подобна объекту. Понятно, однако, что поведение физического объекта определяется не только его геометрией, но и характером воздействия на него внешних объектов, его физическими характеристиками. Поэтому требуется выполнение подобия еще по физическим параметрам. Ясно, что характер протекания физического явления не должен зависеть от выбора единиц измерения физических величин (выберем мы для измерения расстояния метр или другую величину, для измерения времени секунду или период какого-нибудь циклического процесса и т.д.), а определяется безразмерными параметрами, т.е. относительными величинами. В случае подобия явлений все их количественные характеристики, представленные в относительной форме, совпадают. Тождественность всех, признанных существенными, относительных характеристик у модели и оригинала означает соответствие между оригиналом и моделью. Иногда это требование оказывается настолько жестким, что модель оказывается совпадающей с оригиналом. В этом случае некоторые характеристики объекта провозглашаются несущественными, и строится более грубая модель объекта. Представление результатов эксперимента с моделью в относительных переменных позволяет исследованием на одной модели обеспечить изучение целой группы подобных явлений. В пределах этой группы для конкретного объекта численные результаты получаются простым пересчетом, состоящим в умножении на масштабные коэффициенты. При физическом моделировании предполагается физическая однородность объекта и модели, их геометрическое подобие и подобие краевых распределений. Кроме этого, остаются еще требования количественного характера, выражающиеся в равенстве критериев подобия. Критерии подобия — это безразмерные числа, величина которых определяется как произведение степенных функций воспроизводимых (или управляемых) параметров (только степенные функции параметров позволяют сделать их произведение с нулевой размерностью). Приведем примеры. При исследовании общей картины обтекания твердого тела однородным потоком несжимаемой жидкости воспроизводимыми параметрами являются: характерный геометрический размер тела L см, скорость набегающего потока вдали от тела vo м/с, кинематическая вязкость жидкости v см2/с. Эти три параметра связываются в один безразмерный критерий подобия — число Рейнольдса: Re = vo L/v. В модели, воспроизводящей характер обтекания реального объекта, кроме геометрического подобия, требуется выполнить равенство чисел Рейнольдса модели и объекта (только в этом случае структура течения около модели будет подобна структуре течения около объекта):
— где штрихом отмечена величина, относящаяся к объекту, а двумя штрихами — величина, относящаяся к модели. Уравнение (1.1) удобно записать в другом виде
или, вводя множители преобразования воспроизводимых параметров
в виде
Уравнение (1.3) связывает три параметра модели одним уравнением, оставляя большую свободу для построения модели (выбора жидкости, размера тела или скорости потока). Используя ту же жидкость, можно, например, в два раза уменьшить размер модели, одновременно в два раза увеличив скорость течения жидкости. Если, однако, существенным становится еще хотя бы один воспроизводимый параметр, то ситуация может существенно измениться. Пусть, например, обтекаемое тело находится не слишком далеко от поверхности жидкости, и на ее обтекании сказывается сила тяжести. В этом случае появляется по крайней мере еще один воспроизводимый параметр g — ускорение свободного падения и еще один независимый критерий подобия — число Фруда
Требование равенства чисел Фруда для модели и объекта приводит к уравнению
В экспериментах на Земле kg =1 и возникает связь
Уравнение (1.3) с учетом (1.5) приводит к
Это означает, что натурную жидкость (kv = 1) в модели использовать нельзя, поскольку при этом модель становится тождественной натуре (kv = 1, kL = 1). Как сформулировать критерии подобия для произвольной физической проблемы? Если интересующий физический процесс описывается некоторой системой уравнений (с помощью фундаментальных физических законов в разумном приближении удается записать систему уравнений), то переход в этой системе к собственным единицам измерения (к безразмерным единицам) автоматически порождает все критерии подобия задачи. Если такие уравнения не используются, то необходимо выписать все существенные воспроизводимые параметры физического явления и построить независимые безразмерные критерии, подобно тому, как это было сделано выше. Формулировка критериев подобия обязательна при любом моделировании, так как числовые значения именно этих критериев определяют характер протекающего процесса. Отказ от требования физической однородности явлений в натуре и модели расширяет возможности моделирования. Для построения модели можно использовать количественное описание исследуемого явления с помощью алгебраических, дифференциальных или других уравнений и неравенств. Совокупность этих математических соотношений, представляющих обычно сложную математическую задачу, должна отражать существенные стороны моделируемого объекта. Как в этом случае нам удается получить новые знания об объекте? Дело в том, что, пользуясь фундаментальными законами физики, мы можем легко описать поведение объекта на малых интервалах времени и изменение полей, задающих состояние объекта, на малых пространственных масштабах. Наоборот, для целей практики обычно требуется знание интегрального поведения объекта, т.е. изменения его состояния на большом промежутке времени. Таким образом, в модель мы закладываем свои дифференциальные знания об объекте, а в результате экспериментов с моделью получаем некоторые интегральные знания. Метод моделирования в этом случае называется математическим моделированием и сводится к построению решения некоторой обычно сложной математической задачи, его анализу и наглядному представлению результатов исследования. Среди изучаемых явлений и процессов встречаются такие, главным свойством которых является их случайный характер. Наиболее ярким примером такого процесса является блуждание броуновской частицы. Для моделирования подобных процессов используется метод аналогии. В модели воспроизводят случайный характер процесса, имеющий такие же статистические характеристики, какие имеет исследуемый объект. Полученные в результате эксперимента интегральные характеристики модели переносят на объект. Такой метод моделирования называют имитационным моделированием. Важной причиной использования моделей может служить привлечение их как средства обучения и тренажа. Можно сформулировать следующие цели школьного курса моделирования: 1) дать научные основы моделирования (правила построения моделей и экспериментов с ними); 2) углубить знания учащихся в области конкретных наук и придать изучению этих наук творческий характер; 3) при математическом моделировании дать практические примеры использования математических методов, вложив в формальные математические подходы конкретный смысл практической деятельности; 4) разнообразить уроки информатики с помощью решения конкретных вытекающих из практики задач; 5) продемонстрировать возможности современных компьютеров для решения задач, не укладывающихся в офисные приложения. 2. Особенности математического моделированияОдной из наиболее популярных и полезных форм моделей в современной науке являются математические модели. Создавая математическую модель, необходимо установить количественные связи, описывающие свойства объекта или явления. Каждая характерная черта объекта, особенность его поведения должна быть зафиксирована в виде некоторого математического отношения. Наиболее просто связи между характеристиками объекта моделирования устанавливаются на малых промежутках времени и для близких точек пространства. Записывая такие связи, мы обычно приходим к дифференциальным уравнениям или к их конечно-разностным аналогам. Построение математических моделей с использованием дифференциальных уравнений является наиболее распространенным методом в физике, поскольку все основные законы современной физической науки записываются в виде таких уравнений. Дифференциальными уравнениями являются уравнения механики Ньютона и квантовой механики, уравнения гидродинамики, электродинамики и термодинамики. Исследование математических моделей, построенных на базе дифференциальных уравнений или их конечно-разностных аналогах, почти всегда сводится к численному эксперименту или, как говорят, к численному моделированию. Численное моделирование стало важным методом научного исследования в связи с тем, что модели содержат нелинейные уравнения или обладают большим числом степеней свободы (описываются системой уравнений с большим числом переменных) и не поддаются аналитическому анализу. Кроме того, в распоряжении исследователей появилась техника с огромными вычислительными и графическими возможностями — персональные компьютеры. Их использование в математическом моделировании наложило свой отпечаток на характер экспериментального исследования модели. Формулировка задачи для компьютера требует четкого понимания цели численного эксперимента и вопросов, на которые должен дать ответ этот эксперимент. Оперативное графическое представление результатов численного эксперимента на дисплее позволяет сделать результаты наглядными и приблизить численный эксперимент к аналитическому исследованию математической модели. Важной проблемой во всяком моделировании, а при численном — в особенности, является проблема достоверности результатов эксперимента, т.е. правильного описания поведения реального объекта в результатах эксперимента на модели. В численном эксперименте, кроме огрубления реального объекта при переходе к математической модели, вносятся дополнительные ошибки, связанные с приближенным решением сформулированной в модели математической задачи. Контроль за погрешностями в численном эксперименте может быть организован разными способами, но должен присутствовать всегда. Эффективным методом такого контроля можно считать привязку результатов численного эксперимента к нескольким возможным асимптотическим решениям математической задачи или сопоставление результатов численных экспериментов, проведенных разными математическими методами. Последним словом в пользу справедливости результатов моделирования является согласование его результатов с контрольными натурными экспериментами. Каковы основные источники погрешности при моделировании физических задач? Погрешность математической модели. При составлении математической модели задачи учитывают лишь наиболее важные факторы, а многими второстепенными пренебрегают. Например, в большинстве “житейских” задач поверхность Земли считается плоской, а влиянием трения пренебрегается. Но это вовсе не означает, что данные факторы не оказывают никакого влияния, ни тем более того факта, что они никогда не являются существенными. Погрешность исходных данных. Все физические величины и константы либо непосредственно измеряются приборами, либо вычисляются на основе тех или иных измерений. Очевидно, что каждый прибор имеет определенную погрешность измерения. Погрешность численного метода. Любой численный метод аппроксимирует (описывает) решение физической задачи с определенной погрешностью. В частности, большинство физических уравнений имеют дифференциальную форму, которая малопригодна для решения на компьютере; центральная идея в подготовке задачи к расчетам на ЭВМ состоит в замене бесконечно малых разностей малыми, но конечными. Даже на интуитивном уровне понятно, что переход от исчисления бесконечно малых к конечным разностям вносит некоторую погрешность. Погрешность представления чисел в компьютере. Когда мы вводим десятичное вещественное число в компьютер, оно подвергается автоматическому преобразованию в двоичное представление. Данный процесс не всегда возможно произвести точно. Например, “круглое” в десятичной системе число 0,1 при переводе в двоичную систему образует бесконечную дробь, которая принудительно обрывается на каком-либо знаке. Так возникает еще один механизм появления погрешности. Погрешность вычислений функций в компьютере. При вычислении математических функций, таких, как sin(x) или ln(x), используется разложение в ряд. Сумма ряда опять-таки не может быть вычислена абсолютно точно, поскольку процесс вычисления обрывается на определенном слагаемом, а всеми остальными пренебрегается. Погрешность арифметических действий над приближенными значениями. Если произвести арифметическое действие над двумя приближенными числами, то результат тоже будет сохранять определенную погрешность. Рассмотрим в качестве иллюстрации классический пример вычитания двух близких приближенных чисел. Пусть A = 3,84, а B = 3,82, причем их абсолютная погрешность не превышает 0,01 (нетрудно подсчитать, что относительная погрешность в этом случае не более 0,03 %). Тогда разность A – B = 0,02, причем погрешность, равная сумме погрешностей исходных чисел, составит 0,01 + 0,01 = 0,02, т.е. 100 %! Разумеется, в реальных вычислениях ситуация не настолько катастрофическая, но погрешность все равно будет. Несложные рассуждения показывают, что первые две причины не имеют непосредственного отношения к компьютерному моделированию, и уменьшением таких видов погрешности занимаются физики. Что же касается остальных ее разновидностей, то они носят вычислительный характер и представляют с точки зрения нашей публикации определенный интерес. Поэтому рассмотрим вопрос об этих типах погрешностей (и, следовательно, точности результатов численного моделирования) несколько подробнее. Прежде всего отметим, что одной из главных особенностей компьютера является его дискретность. Это означает, что для представления чисел, равно как и любой другой информации, используется конечное число двоичных разрядов. Именно отсюда вытекают почти все особенности “компьютерных” чисел по сравнению с “математическими”. Существует два принципиально разных вида чисел, представленных в компьютере: целые и вещественные. Целые всегда кодируются в машине абсолютно точно, и единственная неприятность, которая может с ними возникнуть, это так называемое “переполнение”, т.е. ситуация, когда имеющихся двоичных разрядов не хватает для записи получившегося числа. Проще говоря, для выбранного типа представления целых чисел их диапазон конечен, в то время как в математике целое число может быть сколь угодно большим. Благодаря достаточно большой разрядности современных процессоров, а также наличию разнообразных форматов целых чисел (“коротких” и “длинных”) данная проблема встает перед рядовым пользователем довольно редко. В частности, даже попытки специально “переполнить” числовую ячейку Excel во многом безуспешны, поскольку тот “в трудной ситуации” незаметно для пользователя автоматически переводит большое число в другой формат, где “потолок” допустимых значений выше (в том числе даже переходит от целочисленных типов к вещественным!). Что касается вещественных чисел, то здесь ситуация заметно хуже. Напомним читателям, что в отличие от дискретных целых чисел множество вещественных чисел является непрерывным. Из этого немедленно следует, что на любом произвольно выделенном отрезке количество вещественных чисел ничем не ограничено (иначе говоря, в математике количество знаков после запятой бесконечно, что опять-таки невозможно полностью смоделировать в машине по причине дискретности). По указанным причинам, при вводе в компьютер вещественные числа должны проходить процедуру дискретизации (сравните с процессом записи звука в компьютере), что делает принципиально невозможным их абсолютно точное представление. Какие практические выводы следуют из изложенной абстрактной теории? · Подавляющее большинство вещественных чисел не может быть представлено в компьютере точно, а значит, их сравнение на равенство некорректно (исключение могут составлять значения с нулевой дробной частью или случаи, когда последняя является степенью двойки, например, 3,25). · Поскольку вещественные числа, вообще говоря, приближенны, результаты любых действий над ними тем более содержат погрешность, причем при большом количестве вычислений погрешность может стать существенной. · Компьютер производит вычисления не идеально точно, поэтому полученные результаты расчетов (особенно сложных) необходимо проверять на достоверность. Приведем конкретные примеры, демонстрирующие наличие вычислительной погрешности различных видов. Пример 1 Запустим следующую простую программу на Паскале. const n=10; var i:integer; s,h:double; begin h:=1/n; s:=0; for i:=1 to n do s:=s+h; writeln(1-s); end. Как ясно из текста программы, она 10 раз складывает дроби 0,1. Из результатов запуска следует, что ответ не равен 1 (несмотря на двойную точность применяемых вещественных чисел!), хотя и отличается от нее всего на 10–16. Пример 2 [7] Допустим, что в качестве упражнения по освоению электронной таблицы Excel учитель предложил ученикам проверить тот факт, что n! = (n–1)! * n. Примерное решение задачи для n = 5 может выглядеть следующим образом:
Примечание. На всякий случай напомним читателю, что запись n!, в математике называемая “красивым” термином “факториал”, есть просто произведение последовательных целых чисел от 1 до n. Например, 5! = 120. Аккуратно внесем формулы в электронную таблицу, и Excel послушно подтвердит, что все правильно, написав “да” в ячейке D3. А если взять другое число, допустим, 25? К нашему удивлению, появится результат, изображенный на рис. 2.1.
Рис. 2.1 Неожиданным здесь является то, что ячейка C3, вычисленная как разность C1 – C2, вроде бы равняется нулю, но проверка в клетке D3 утверждает, что это не так! Все дело в том, что 25! достаточно большое число и в ходе вычислений имеющейся разрядной сетки становится недостаточно для полного сохранения результатов; приходится последние (наименее важные) разряды округлять. Результат тем более удивителен, что из условия задачи кажется, что компьютер должен оперировать исключительно с целыми числами и никакой погрешности возникать не должно! На самом же деле из-за большой величины результаты преобразованы в вещественную форму (о чем красноречиво говорит запись 1,55E+25). Пример 3 В школьной физике при решении задачи ответ очень часто представляется в виде дроби, в числителе и знаменателе которой стоит произведение известных физических величин и констант. Сколько правильных цифр получится в ответе, если наименьшее число значащих цифр в одном из данных равно 3? Из строгой математической теории погрешности [8] следует, что не более трех, как бы ни точны были все остальные данные! И сколько бы разрядов не использовалось при компьютерных вычислениях, ситуация принципиально не может быть улучшена. Практический вывод таков: никакая точность вычислений не может получить больше знаков, чем имеет самое “грубое” из начальных данных. Пример 4 Рассмотрим решение простого уравнения x = 0,5 x2 + 0,01 методом итераций. Зададим в качестве начального приближения x0 три близких значения — 1,98, 1,99 и 2. В итоге получим три разных поведения функции. В первом случае значения устремятся к корню уравнения, равному 0,01. Во втором случае график уйдет вверх после весьма продолжительного горизонтального участка, наконец, третий начнет расти практически сразу же. Итак, мы видим, что при вычислениях по весьма примитивной формуле для трех достаточно близких чисел результаты носят качественно разный характер. Данный пример показывает, что вычислительный метод может оказывать существенное влияние на получение решения. В заключение этого параграфа сформулируем кратко, на какие этапы можно условно разделить весь процесс математического моделирования с использованием численного эксперимента. 1. Начать моделирование нужно с обсуждения физической проблемы и постановки вопросов, на которые следует получить ответ. 2. Для физических величин, появившихся при этом обсуждении, написать управляющие уравнения, используя фундаментальные законы или знания о дифференциальных свойствах исследуемого процесса. Необходимо убедиться в математической полноте сформулированной задачи. 3. Выбрать характерные масштабы для переменных и записать уравнения в безразмерном виде. Выбрать независимые критерии подобия задачи. 4. Переформулировать математическую задачу на языке алгебры и выбрать метод ее решения. 5. Составить алгоритм численного эксперимента. 6. Записать алгоритм на алгоритмическом языке и провести пробные вычисления для проверки работоспособности выбранного метода. При неудаче вернуться к п. 4. 7. Провести численный эксперимент для широкого диапазона значений критериев подобия. Выделить те из них, при которых происходит смена режимов в исследуемых физических процессах. 8. Подвергнуть критическому анализу все полученные результаты, сравнить их с известными натурными экспериментами. Рассмотреть возможные пути улучшения модели, если результаты в каком-либо смысле оказались неудовлетворительными, или упрощения модели, если численный эксперимент оказался трудоемким. В дальнейшем мы перейдем к конкретным примерам, на которых будут проиллюстрированы основные проблемы численного моделирования.
3. Организация физического моделирования в среде DelphiСовременная визуальная система программирования Delphi предоставляет удобное средство для создания среды моделирования любой физической задачи. Ее визуальная часть, будучи необычайно простой и естественной, позволяет быстро и без особых усилий создать на экране компьютера современный диалоговый интерфейс, который не уступает применяемому в профессиональном программном обеспечении. Лежащий в основе системы алгоритмический язык Паскаль является классическим учебным языком, так что запрограммировать на нем небольшую вычислительную задачу не представляет особой трудности. Наконец, встроенные в систему стандартные компоненты для поддержки таблиц и графики служат приятным дополнением к перечисленным выше достоинствам. По Delphi выпущено огромное число весьма объемных книг, поэтому среди целей нашей публикации не будет подробного описания системы и простейших приемов взаимодействия с ней с помощью мыши. В то же время отдельные важные вопросы программирования в системе (например, связанные с организацией структуры пакета из нескольких проектов, имеющих значительную общую часть, и с оптимизацией рисования графиков), напротив, будут описаны максимально подробно. Иными словами, при изложении материала предполагается достаточным знание читателями основных правил записи программы на языке Паскаль и простейшие навыки работы с Delphi, но ничего сверх этого не потребуется. Заметим, что существует вариант организации данного практикума и без знания программирования — можно просто загрузить с сайта редакции и использовать для моделирования готовые исполняемые файлы. Тем не менее, по мнению авторов, знание хотя бы основ программирования для физика-исследователя весьма желательно, так что мы надеемся, что данный раздел публикации также окажется востребован образовательной общественностью. Учитывая, что целью данной публикации является реализация не одной физической модели, а их целого комплекта, следует особенно тщательно спланировать разработку среды моделирования: необходимо максимально упростить создание последующих программ путем выделения стандартных операций (построение таблиц значений и графиков) в автономные модули с удобным интерфейсом. Подчеркнем, что в учебной литературе подобным вопросам уделяется мало внимания. В самом деле, при выполнении первых упражнений справедливо предполагается, что они простые и автономные, а также что в дальнейшем тексты их программ едва ли войдут без изменения в качестве составной части в другие задачи. Следовательно, средства Delphi для модульного программирования и создания комплексов похожих программ остаются “за кадром”. В нашем случае ситуация иная. Мы предполагаем разработать единый пакет программ, которые похожи по функциональности и интерфейсу, что, напротив, открывает большие возможности для унификации и повторного использования уже написанных программных блоков. Итак, обсудим наиболее общие вопросы моделирования физических задач в системе Delphi, которые будут использоваться во всех разработанных в публикации примерах. Построение графиков в системе Delphi В научных исследованиях процесс получения результата часто имеет не меньшее значение, чем собственно результат. Поэтому мы сочли полезным и поучительным продемонстрировать все этапы решения задачи построения графиков в системе Delphi, а не просто сразу описать готовую программу, в которой все уже заранее предусмотрено. Итак, рассмотрим некоторые характерные проблемы, которые последовательно возникают при построении графиков результатов расчетов на экране дисплея. Проблема 1. Как пересчитывать координаты? Система целочисленных координат дисплея и вещественная декартова система координат устроены не совсем одинаково.
Рис. 3.1 Тем не менее получить формулы масштабирования для перевода физической величины в координаты пикселей дисплея не очень сложно. Выведем, пользуясь рисунком, формулы для пересчета физических координат a и f (аргумент и функция) в экранные x и y для некоторой произвольной точки. Определим сначала физические размеры окна, которое будет отображаться на экране:
Используя пропорциональность в направлении оси x, можно записать:
Отсюда немедленно получается, что
Аналогичным образом
Записанная выше формула для y'не является окончательной для y, поскольку в отличие от оси абсцисс ось ординат на экране имеет противоположную направленность. Для пересчета достаточно несложной формулы
Подставляя в нее выражения для y' и
Таким образом, используя формулы (3.1) и (3.2), можно координаты любой точки пересчитать в координаты соответствующего ей пикселя на экране. Поскольку стоящее в правой части выражение вещественно, а координаты экрана являются целыми числами, не надо забывать добавлять в итоговые формулы функцию round(). Проблема 2. На чем рисовать? Для создания графических изображений многие визуальные компоненты Delphi имеют специальное свойство Canvas (по-русски — холст, картина, канва, т.е. основа). Это объект, который содержит в себе все, что необходимо для рисования (система координат, цвета, кисть, перо, шрифт, режимы рисования и прочие графические атрибуты Windows). Холст есть, например, у компонентов Form, Label, Listbox, Combobox, Image, но его нет у MainMenu, Button, Edit, Panel, Bitbtn. Из этого формально следует, что нанести рисунок можно поверх любого из компонентов, входящих в первую группу, и принципиально нельзя на перечисленные во второй. Но все ли компоненты одинаково хороши для рисования? Для проверки проведем несложный эксперимент. Создадим на форме Form1 три компонента: Image1, ListBox1 и Button1. В обработчик события OnButtonClick стандартным образом внесем следующую простую программу with Form1.Canvas do begin MoveTo(0,0); LineTo(50,50) end; with Image1.Canvas do begin MoveTo(0,0); LineTo(50,50) end; with ListBox1.Canvas do begin MoveTo(0,0); LineTo(50,50) end; Нетрудно догадаться, что эта программа должна нарисовать три наклонных линии: на самой форме и на холстах компонентов Image1 и ListBox1. Запустим приложение и щелкнем по кнопке Button1: как и ожидалось, возникнут три линии. Теперь “первым попавшимся” окном закроем часть рисунка (обязательно отпустите кнопку мыши, иначе изменения на экране не зафиксируются!). Наконец, отодвиньте “верхнее” окно немного в сторону, и вы увидите примерно такую картину, как на рис. 3.2.
Рис. 3.2 На ней отчетливо видно, что части линий, которые были закрыты окном, на самой форме (вверху) и на компоненте ListBox1 (внизу) исчезли, тогда как компонент Image1 заботливо восстановил свое содержимое. Вывод очевиден: для целей рисования нам лучше всего подходит компонент типа Image. Примечание. Строго говоря, некоторый механизм “самовосстановления” рисунка на холсте в Delphi предусмотрен. Для этого можно программу рисования поместить в обработчик события OnPaint (он есть не у всех компонентов, но у формы такое событие существует). В этом случае после перерисовки компонента Windows передаст управление вашему обработчику и тот восстановит рисунок на холсте. Для наших физических применений данный механизм абсолютно неприемлем, поскольку он потребует при каждой перерисовке окна пересчитывать все графики! Итак, в качестве холста для рисования графиков мы выбираем компонент типа Image. Очень удобно свойству выравнивания Align установить значение alClient — тогда наш компонент будет всегда автоматически растягиваться на всю площадь окна. .0Проблема 3. Как построить график? Первый вывод, касающийся способа рисования графиков, для физических задач довольно очевиден: строить график рассчитываемой величины удобнее всего по точкам. В Delphi имеется для этого хорошо подходящий для этого механизм: объект Canvas содержит в себе свойство Pixels, представляющее собой массив, образующий рисунок пикселей. Поставить точку — значит присвоить элементу массива необходимое цветовое значение типа TColor, например: Image1.Canvas.Pixels[x,y] := clBlack; В приведенном операторе x и y — координаты точки экрана, а значение константы clBlack обозначает черный цвет (первые две буквы подчеркивают то обстоятельство, что это именно цвет — color). Кодирование цветов в Delphi заслуживает того, чтобы о нем рассказать подробнее. Стандартные 16 цветов, как мы уже видели на примере черного, имеют специальные имена, начинающиеся с префикса “cl”. Их названия приведены в таблице.
Небольшим темным пятном на фоне полной ясности в стандартных цветах служит тот факт, что в Windows их почему-то не 16, а 20. Причем, как написано в книге [9], “Когда Windows сбрасывает системную палитру, то он загружает стандартные цвета в первые 10 и последние 10 позиций. Каждое окно всегда может рассчитывать на эти 20 цветов независимо от того, какие цвета загружены в оставшуюся часть системной палитры”. Разумеется, можно определить и свой собственный RGB-цвет, как показано ниже. const clMyColor = TColor($FFFBF0); И еще об одной особенности определения цветов в Delphi. Если посмотреть на установленный по умолчанию цвет формы, то он, как ни удивительно, не совпадет ни с одним из перечисленных выше стандартных цветов: в графе color вы найдете весьма необычную надпись clBtnFace (цвет лицевой стороны кнопок). Этот и множество других имеющихся в списке цветов (clActiveCaption, clInactiveCaption, clMenu, clWindow, clWindowFrame и др.) берутся из цветовых настроек Windows. Если не боитесь на время увидеть на экране своего дисплея сильно “испорченную” цветовую гамму, можете провести следующий эксперимент. Обычным образом (правой кнопкой щелкнуть по Рабочему столу и выбрать в меню Свойства) перейдите к настройкам свойств экрана. На вкладке Оформление щелкните по рисунку кнопки; в ответ на это Windows сообщит, что он готов к настройке “рельефных объектов”. Щелкните по выпадающему списку Цвет, и появится стандартная цветовая палитра из 20(!) цветов, причем по умолчанию выбран серый (именно такой цвет имеет левый нижний квадратик). Если щелкнуть по соседнему справа цвету, то после нажатия традиционного OK все кнопки, а с ними и множество элементов окон, окрасятся в изумительный голубоватый оттенок (и это еще один из самых спокойных цветов!).
Рис. 3.3 Прежде чем восстановить цветовую гамму, не забудьте открыть Delphi и убедиться в том, что там тоже поменялись цвета. Теперь попытаемся вернуть цвета в старую добрую цветовую схему. Не тут-то было! Установка старого цвета рельефных объектов вернет назад не все цвета! Остается в списке Схема выбрать значение Стандартная — только тогда буйство красок окончательно исчезнет. Таким образом, если только вы не хотите, чтобы ваше приложение меняло окраску в соответствии с не всегда здоровыми цветовыми вкусами пользователей Windows, устанавливайте стандартные значения цветов, перечисленные в приведенной выше таблице. Теперь, когда мы в теории поняли, как можно рисовать цветные графики, перейдем к их построению на практике. Для простоты выберем “классическую” функцию y = sinx и попытаемся нарисовать ее график так, чтобы он занял всю отведенную ему площадь окна. Поместим на форму компонент Image1 и установим ему свойство Align = alClient, чтобы он занял всю рабочую площадь окна. Затем добавим еще три кнопки: Button1, Button2 и Button3, первая из которых будет инициировать построение графика, вторая — очистку окна, а третья — принудительно прекращать вычисления. Займемся пока первой кнопкой. Добавим в ее обработчик события OnClick следующую программу: procedure TForm1.Button1Click(Sender:TObject); const da=0.001; var x,y,w,h:integer; a,p:double; begin w:=Image1.Width; h:=Image1.Height; a:=0; p:=2*pi; while a<p do begin x:=round(w*a/p); y:=round(h*(1-sin(a))/2); Image1.Canvas.Pixels[x,y]:=clBlack; a:=a+da; end; end; В ней нетрудно найти уже знакомые нам
фрагменты: окраску пикселя и расчет его
координат по формулам (3.1) и (3.2). В самом деле, для
функции sinx имеем amin = 0, Пожалуй, остается объяснить роль и влияние константы da. Данное число влияет на то, сколько точек будет рассчитываться при построении графика: если задать большое значение, то точек будет мало и график получится прерывистый. Чем больше точек, тем лучше качество графика, но тем дольше он считается. Кроме того, при достаточно малом значении da увеличение количества точек уже не меняет вида графика. Указанный в тексте программы шаг близок к оптимальному: и считает быстро, и график вполне аккуратный.
Рис. 3.4 Заметим, что в примерах по построению графиков на экране дисплея в книгах часто описывается несколько иной алгоритм. Он заключается в том, что для каждого пикселя по горизонтали производится перевод значения в естественные единицы измерения, затем от полученного значения вычисляется функция, результат снова пересчитывается в пиксели и наносится на график. Такой “машинный” алгоритм менее удобен для рассматриваемого нами круга задач, чем описанный выше “математический” алгоритм, когда за основу берутся естественные значения аргумента и функции. Кроме того, как следует из теории, “машинный” алгоритм позволяет получить непрерывный график только для линий, составляющих с осью x угол не более 45°. Примененный нами способ свободен от указанного недостатка и строит более наглядный график, а также дает меньшую вычислительную погрешность. И не забудьте провести с программой еще один эксперимент. Обязательно убедитесь в том, что если увеличить размер окна, то программа автоматически пересчитает масштаб и снова аккуратно “растянет” график на всю площадь окна. Проблема 4. Как рисовать по ходу вычислений? Несмотря на определенные успехи, достигнутые в деле рисования графиков, некоторая проблема все-таки осталась. Дело в том, что если задать, например, da = 0.00001, то даже на процессоре с тактовой частотой более двух гигагерц время счета станет значительным (а у нас нет причин заранее быть уверенными в том, что “долгие” расчеты в физической задаче выполнять не придется!). И в указанной ситуации поведение программы становится весьма неудобным: она долго-долго считает без всяких видимых изменений на экране и только затем выводит весь готовый график целиком. Нельзя ли сделать так, чтобы график рисовался по ходу вычислений? Конечно, можно, но сначала надо разобраться, почему поведение программы именно такое, как мы наблюдаем. Для этого придется обратиться к теории. Известно (см., например, [10, 11], а также публикацию в прошлогодних номерах газеты [12]), что функционирование среды Windows построено на пересылке и обработке сообщений. Кстати, даже сама структура программы в Delphi говорит нам об этом: вместо единой программы в Паскале для MS DOS в Delphi мы имеем набор процедур, каждая из которых есть не что иное, как обработчик сообщения о том или ином событии. Как свидетельствует опыт, по умолчанию исполнение программы происходит таким образом, что все сообщения обрабатываются по мере поступления строго последовательно. Это означает, что, пока не завершена полностью обработка одного события, следующее обрабатываться не будет. В этом и заключается объяснение поведения нашей программы рисования: вычисления “миллионов синусов” занимают заметное время (с точки зрения Delphi эти вычисления есть обработчик щелчка по кнопке Button1), и только после полного завершения вычислений система переходит к обработке следующего события, связанного с обновлением рисунка на компоненте Image1. Казалось бы, дело безнадежно, поскольку изменить логику работы системы мы не сможем. Тем не менее выход из положения есть — создатели Delphi предусмотрели подобные потребности программистов. В объекте Application (приложение), который ассоциирован с нашей программой, имеется метод ProcessMessages, смысл которого состоит во временном прекращении работы “длинного” обработчика и передаче управления Windows для обработки “накопившихся” в очереди сообщений; после обработки очередного сообщения Windows возвращается к выполнению прерванного ранее обработчика. Следовательно, периодический вызов указанного метода решит сформулированную проблему: проделав часть вычислений, система нарисует готовую часть графика и затем процесс продолжится. Оказывается, добавив в конец цикла вычисления while единственную строку Application.ProcessMessages; мы избавимся от проблемы. Кстати, попутно появляется возможность решить и еще одну проблему — аварийное прерывание “затянувшихся” вычислений. Это проблема того же сорта: надо обеспечить обработку нажатия кнопки Стоп, пока не завершился счет. Как только в программе появился вызов метода ProcessMessages, возможность для прерывания счета уже создана. Программная реализация проста: описываем глобальную (т.е. доступную всем обработчикам) логическую переменную stop и перед началом цикла вычислений присваиваем ей значение false. Нажатие кнопки аварийного завершения Button3 установит эту переменную в true. Остается дополнить условие повторения цикла следующим образом: while (a<p) and not stop do — и вычисления будут прекращаться или по значению аргумента a, или по переменной stop. Если вы по какой-либо причине затрудняетесь найти те места в программе, куда нужно вставить описанные в данном разделе дополнительные строки, обратитесь к полному тексту программы, приведенному в следующем разделе, посвященном ускорению процесса. Обязательно протестируйте механизм аварийной остановки, предварительно задав большое значение переменой da (при малых da произвести тестирование будет трудно — см. следующую проблему). Проблема 5. Как ускорить процесс? Увы, еще не все наши проблемы позади. Оказывается, введенные в предыдущем разделе изменения хотя и обеспечили нужное поведение программы, но ее работа во много раз замедлилась! Более того, если шаг изменения аргумента da мал, то компьютер ведет себя так, как будто он “завис”: например, мы нажимаем кнопку закрытия нашего приложения, а оно не реагирует! Что же произошло? Перед нами типичный случай, когда вера в неограниченное могущество компьютера оказывается необоснованной, а применение алгоритма решения задачи “в лоб” приводит к тому, что наш интеллектуальный помощник элементарно не справляется с объемом работ. Уместно подчеркнуть, что недалекие пользователи в подобных ситуациях немедленно бегут в магазин за новым, более мощным компьютером. Нам кажется, что читатели газеты не из их числа, а наградой за их интеллектуальную пытливость будет несложное усовершенствование программы, которое позволит вполне комфортно работать и, кстати, отложить поход за новым компьютером до более оправданного случая. Итак, почему же все-таки наша программа после внесенного усовершенствования стала “тормозить” компьютер? Логично предположить, что это как-то связано с графикой, поскольку количество вычислений осталось без изменения. Если раньше машина рисовала всего один график (после завершения вычислений), то сейчас обновление рисунка происходит после каждого цикла. Как наносятся новые точки на рисунок? В многочисленных книгах по освоению Delphi о таких вещах обычно не пишут. Обдумав общую логику работы графики в Windows [10], можно высказать весьма правдоподобную гипотезу о том, что рисунок компонента Image на самом деле хранится в ОЗУ и при всяком обновлении копируется на экран целиком. В пользу этой гипотезы говорит и следующее соображение: если рисунок в памяти обновляется попиксельно, как это делается в нашей задаче, то едва ли проще “возиться” с поиском каждого из них в видеопамяти — лучше обновить нужные пиксели в ОЗУ и с помощью какой-нибудь оптимизированной аппаратной процедуры копирования перебросить туда весь блок данных. Проверим, насколько справедлива наша гипотеза. Если копирование холста из ОЗУ в видеопамять происходит долго, то желательно уменьшить число копирований пусть даже ценой усложнения логики программы. По-видимому, оптимальным способом для этой процедуры будет являться следующий. При малом шаге по аргументу вычисленные значения часто попадают в одни и те же точки. Ясно, что повторное рисование точек картинки не портит, но время занимает. Попробуем на этом сэкономить. Итак, будем запоминать координаты последнего поставленного на экране пикселя и, если новая точка попадает в то же самое место, не будем вносить напрасные изменения в массив Image1.Canvas.Pixels, провоцируя тем самым абсолютно бесполезную его перерисовку. Для хранения координат предыдущего нарисованного пикселя в программу введем дополнительные переменные xold и yold. Их начальные значения стоит задать равными несуществующему значению (например, –1), чтобы гарантировать рисование самой первой точки. В дальнейшем после нанесения каждой новой точки необходимо обновлять значения этих переменных. Все предлагаемые изменения несложно найти в приводимом ниже листинге программы (в методе Button1Click). Полный текст программы var stop:boolean; procedure TForm1.Button1Click(Sender: TObject); const da=0.001; var x,y,xold,yold,w,h:integer; a,p:double; begin w:=Image1.Width; h:=Image1.Height; xold:=-1; yold:=-1; a:=0; p:=2*pi; stop:=false; while (a<p) and not stop do begin x:=round(w*a/p); y:=round(h*(1-sin(a))/2); if (x<>xold) or (y<>yold) then begin Image1.Canvas.Pixels[x,y]:=clBlack; xold:=x; yold:=y end; a:=a+da; Application.ProcessMessages end; end;
procedure TForm1.Button2Click(Sender: TObject); begin Image1.Canvas.FillRect(Rect(0,0,Image1.Width,Image1.Height)); end;
procedure TForm1.Button3Click(Sender: TObject); begin stop:=true end; Введение данного несложного контроля приводит к неожиданно хорошему результату: нормальная скорость рисования обеспечивается при любых, даже очень малых шагах по аргументу da. Интересно, что использованная нами идея является принципиально важной при проектировании визуальных компонентов. В частности, в книге [13] при объяснении принципов разработки методов записи для компонентов указано: “Обратите внимание в приведенном выше методе на то, что данное свойство модифицируется только если новое значение отличается от текущего. Подобный тип обработки очень распространен в методах записи и помогает избежать ненужных присвоений и избыточных побочных эффектов, которые в противном случае привели бы к значительным потерям времени обработки”. Таким образом, логический анализ проблемы позволил найти достаточно простое ее решение. Даже если гипотеза о хранении образа в ОЗУ все же не совсем верна, тем не менее рассуждения о сути процесса все равно привели нас к правильному результату. Примечание. Впервые описанный эффект резкого замедления работы компьютера был замечен при отладке задачи про движение спутника. Оказалось, что время расчетов при указанной модернизации программы уменьшилось с 8,5 минут до нескольких секунд! Проблема 6. Как очистить графики? Это небольшая самостоятельная проблема, которая решается относительно просто. Объект Canvas имеет множество встроенных методов рисования (линий, эллипсов и т.п.). Один из них — рисование заполненного прямоугольника FillRect — хорошо подходит для наших целей. Единственной тонкостью применения этого метода является способ задания границ закрашиваемой области. В Delphi для подобных целей используется специальный тип данных TRect (от англ. rectangle — прямоугольник), который задает левую верхнюю и правую нижнюю вершины прямоугольника. Простейшим (но не единственным) способом получить структуру TRect служит специальная функция Rect, аргументы которой являются целочисленными координатами необходимых точек. В итоге окончательная строка, которую следует поместить в обработчик кнопки Button2, для полной очистки холста примет вид: Image1.Canvas.FillRect(Rect(0,0,Image1.Width, Image1.Height)); Проблема 7. Как изобразить итоговый график? При построении всех предыдущих графиков мы довольствовались закраской отдельных пикселей на компоненте Image, поскольку точек на каждой линии (траектории) вычислялось заведомо достаточно для построения кривой любой сложности (в действительности нам, наоборот, приходилось принимать специальные меры, чтобы на график наносились не все точки, — см. проблему 5). При построении итогового графика зависимости некоторой интегральной характеристики от параметра задачи ситуация качественно иная: точек на нем ровно столько, сколько произведено расчетов. Следовательно, количество точек невелико, и надеяться на то, что их всегда будет достаточно для построения “сплошного” графика, не приходится. Итак, нам потребуется разработать еще один способ отображения графических зависимостей для случаев, когда число известных точек невелико. Для решения поставленной задачи в Delphi предусмотрен специальный демонстрационный компонент Chart, который отличается тем, что позволяет легко строить диаграммы и графики самых разнообразных видов. По своим функциональным возможностям данный компонент во многом напоминает мастер диаграмм MS Excel. Для создания Chart необходимо найти его на странице Additional палитры компонентов:
Рис. 3.5 Далее стандартным образом поместим его на форму и проделаем необходимые простейшие настройки. Компонент имеет специальный редактор, вызываемый двойным щелчком мыши по его изображению. Вид окна редактора показан на рис. 3.6.
Рис. 3.6 Первое, что обязательно нужно сделать, это создать серию данных для графика (по умолчанию система назовет ее Series1). Для осуществления названного действия щелкните по кнопке Add; возникнет новое диалоговое окно, в котором редактор “рекламирует” все свои возможности:
Рис. 3.7 Обязательно обратите внимание на следующую деталь. При появлении окна флажок 3D в нижней части окна выбран, так что картинка изображает трехмерные варианты графиков. Для физических целей плоских вполне достаточно, и, прежде чем снять с экрана приведенную в статье картинку, данный флажок был сброшен. Конечно, при рисовании может быть использован любой из имеющихся типов, но мы воспользовались последним: он называется bubble (в переводе с английского — “пузырек”) и наносит на плоскость точки в виде кружков заданного радиуса и цвета. Обратите внимание, что после обычного завершения диалога нажатием OK в окне редактора появится серия Series1. Прежде чем закончить с ней работу, установим несколько свойств, что позволит увеличить место, занимаемое графиком, путем отказа от всяческих подписей и пояснений. Делается это несложно. Щелкнем по закладке страницы Legend (“легенда”, или по смыслу лучше “обозначения”) и сделаем ее невидимой путем сброса флажка Visible (видимая) — см. рис. 3.8.
Рис. 3.8 Находившиеся справа подписи исчезнут, а площадь под график увеличится. Аналогичным образом на странице Titles сделаем невидимым синий заголовок TChart (данная “эстетическая” коррекция может показаться читателям не самой лучшей, но мы намерены ограничиться подписью в заголовке формы). Перейдем к написанию программы. Договоримся, что данные для обобщающего графика мы будем брать из табл. 1, куда после расчета каждой траектории заносятся ее интегральные характеристики. Данная таблица расположена на форме form3 и называется StringGrid1. Ради универсальности введем константы Narg и Nfunc, которые будут задавать номера столбцов аргумента графика и функции соответственно. Для извлечения необходимого значения из (строковой!) таблицы и преобразования его в число напишем следующую функцию. function getNumber(k,y:integer):double; var s:string; {аргумент/функция} begin if k=0 then k:=Narg else k:=Nfunc; {содержимое ячейки} s:=form3.StringGrid1.Cells[k,y];{замена десятич. '.' на ','} k:=pos('.',s); if k<>0 then s[k]:=',';{результат - вещественное число} getNumber:=strToFloat(s) end; Функция содержит два входных параметра; первый — (k) равен 0 при извлечении аргумента и 1, когда требуется получить из таблицы значение функции; второй параметр y есть просто номер необходимой строки. Функция выбирает необходимую константу с номером столбца, извлекает требуемое строковое значение, заменяет десятичную точку в изображении числа на запятую (русская версия разделения целой и дробной части) и, предварительно преобразовав строку в числовую форму, выдает полученное значение в качестве результата функции. Таким образом, все технические детали извлечения чисел из таблицы оказываются локализованными внутри рассмотренной функции. Теперь опишем, как программировать работу с компонентом Chart. Прежде всего необходимо “связать” созданную нами серию данных Series1 с компонентом Chart1: series1.ParentChart:=Chart1; Далее с помощью метода Clear очистим значения серии и, пока строки табл. 1 не пусты, будем дополнять точки в набор Series1 вызовом метода AddBubble. Последний имеет 5 аргументов, так что стоит их хотя бы кратко прокомментировать. 1. Значение аргумента для точки графика. 2. Значение функции для точки графика. 3. Радиус кружка, изображающего точку (обратите внимание: не в пикселях, а в масштабе графика; с этим еще придется повозиться!). 4. Подпись под каждой точкой; мы выбрали значение аргумента, преобразовав его в строковое представление стандартной функцией FloatToStr. 5. Цвет точки; мы выбрали красный. В итоге получаем следующий рабочий цикл заполнения набора Series1. n:=1; while form3.StringGrid1.Cells[Nfunc,n]<>'' do {пока есть числа} begin addBubble(getNumber(0,n), getNumber(1,n),radius, floatToStr(getNumber(0,n)),clRed); n:=n+1 {к следующей строке таблицы 1} end; После занесения значений компонент автоматически выбирает масштаб и рисует все входящие в него точки. Остается последняя проблема — выбор значения для переменной radius. Ее нельзя задать константой, поскольку “пузырек” масштабируется так же, как и график, т.е. его видимый размер оказывается зависящим от значений функции, по которым строится график. Это, конечно, неудобно и порой приводит к тому, что точки просто исчезают — таким маленьким оказывается их радиус. Универсальное решение проблемы, по-видимому, невозможно. Наиболее разумно связать размер точек с областью изменения функции (она равна fmax – fmin) и взять определенную часть от нее. Экспериментальная проверка, однако, показала, что реализованный по такой методике автоматический выбор не всегда рекомендует удачный размер. Поэтому мы добавили пользователям возможность изменять некоторый множитель, который влияет на размер точек. Мы не будем здесь приводить программу поиска максимума и минимума в столбце таблицы (ее главная сложность — использование для извлечения значений функции getNumber(1,n); остальное очевидно любому, кто изучал программирование). Покажем только заключительные формулы. {автоматический выбор радиуса рисования точек} radius:=max-min; if radius=0 then radius:=max; {ручная коррекция - множитель берется из списка} radius:=(comboBox1.ItemIndex+1)*0.002*radius; С учетом полученной коррекции почти всегда удается получить график удовлетворительного вида. Единственным замеченным нами случаем “неразумного” поведения компонента является построение графика функции, которая близка к константе. В этом случае картина выглядит, например, так, как на рис. 3.9 (проект, посвященный модели атома по Томпсону).
Рис. 3.9 К сожалению, ситуация принципиально не улучшаема, поскольку таков алгоритм выбора масштаба компонентом Chart: при расстановке точек он отображает пространство между “верхом самой верхней точки” и “низом самой нижней”, а они все на одной горизонтали. В итоге изменение размера точек приводит лишь к пересчету масштаба по оси ординат, а неудачный вид графика, когда всю его площадь занимают точки, сохраняется. Полный вид процедуры рисования графика с помощью компонента Chart приведен в распечатке модуля 5 (см. далее). Работа с таблицами в среде Delphi В Delphi предусмотрены специализированные компоненты для работы не только с графиками, но и с таблицами. Их использование существенно облегчает представление данных в табличной форме. Для целей моделирования физических задач требуется главным образом занесение данных в таблицу (самое сложное действие в нашем практикуме — последующее извлечение данных из таблицы для построения итогового графика, о чем шла речь в предыдущем разделе), так что предусмотренных в компонентах стандартных возможностей более чем достаточно. На странице Additional палитры компонентов Delphi имеются две “заготовки” для работы с таблицами — StringGrid и DrawGrid. Во второй компонент заложены некоторые дополнительные возможности (например, в его ячейках предусмотрен объект Canvas, а значит, там можно рисовать!), но они явно выходят за рамки наших потребностей, поэтому мы ограничимся более простой, чисто строковой “сеткой” StringGrid.
Рис. 3.10 Будучи помещенным на форму, компонент StringGrid имеет вид весьма представительной таблицы:
Рис. 3.11 На ней не только предусмотрено место для данных с возможностью прокрутки, но и даже выделенные серые клеточки для оформления подписей строк и колонок (данные столбцы и колонки в Delphi называются fixed — фиксированными, и их число легко регулируется заданием значений свойств FixedCols и FixedRows). Для организации доступа к таблице в ней предусмотрено специальное свойство Cells, представляющее собой обычный (строковый!) двумерный массив. Первый индекс обозначает номер столбца (координата x), а второй — строки (координата y); нумерация начинается с нуля, фиксированные ячейки учитываются. Например, запись Cells[1,2] адресуется к ячейке во втором столбце и третьей строке (на рис. 3.11 она находится непосредственно под выделенной темным цветом клеткой). Приведем пример простой программы заполнения таблицы. Как и для демонстрации графических возможностей, обратимся к простой функции sin x и “затабулируем” ее на отрезке, равном периоду. Договоримся для простоты разбить отрезок на 10 равных частей. Решение сформулированной задачи реализуется следующим несложным образом. На форму помещается компонент StringGrid1, затем двойным щелчком по свободному месту формы создается обработчик события OnFormCreate. Далее в него вписывается следующая программа. procedure TForm1.FormCreate(Sender: TObject); const n=10; var x,y,h:double; i:integer; begin with StringGrid1 do begin ColCount:=2; Cells[0,0]:=' X'; Cells[1,0]:=' Y'; end; h:=2*pi/n; for i:=0 to n do begin x:=i*h; y:=sin(x); with StringGrid1 do begin if i+1=StringGrid1.RowCount then{добавить строку} RowCount:=RowCount+1; Cells[0,i+1]:=FloatToStrF(x,ffFixed,5,4); Cells[1,i+1]:=FloatToStrF(y,ffFixed,5,4); end end end; Программа достаточно проста. Сначала формируется таблица из двух столбцов (по умолчанию Delphi устанавливает больше) и ее “шапка”. Затем вычисляются значения функции sin x для 11 точек (обратите внимание, как организован вычислительный процесс через индексную переменную i!) и заносятся в соответствующие клетки таблицы. Важно подчеркнуть, что видимых на экране ячеек в какой-то момент перестанет хватать, тогда предусмотренный в теле цикла условный оператор аккуратно будет добавлять по одной строке по мере надобности. Особо хочется сказать о функции FloatToStrF, которая позволяет не только выполнить требуемое для таблицы преобразование числа в строку, но и установить при этом его формат. Мы выбрали представление с фиксированным размещением запятой и отобразили после нее 4 знака. В результате на экране появилась вполне симпатичная табличка (рис. 3.12).
Рис. 3.12 Таким образом, работа с таблицей оказывается в среде Delphi простой и удобной. Наличие хорошо проработанного стандартного компонента позволяет не особенно задумываться над табличным представлением результатов и полностью сосредоточить свое внимание на организации вычислений. Примечание. В программах, разработанных в Delphi, при вводе дробных чисел в поля компонентов целую и дробную части следует разделять символом, который определяется национальными настройками ОС Windows, а именно: в русской версии необходимо использовать запятую, а в английской — точку. Для языка программирования подобное решение проблемы кажется несколько непоследовательным (согласно их синтаксису, в вещественных числах всегда однозначно используется точка); тем не менее, если вспомнить электронные таблицы Excel, то там тоже имеет место аналогичный “двойственный” подход. Общая структура практикума (пакета программ) Обсудим теперь проблемы структуры нашего программного комплекса для моделирования нескольких физических задач; для краткости будем называть всю совокупность программ практикумом, а каждую входящую в него задачу проектом (последний термин напрямую заимствован из Delphi). Будем считать, что моделирование типичной школьной физической задачи в среде Delphi протекает следующим образом. В результате предварительного обсуждения уже выработана математическая модель, т.е. выписаны все необходимые расчетные формулы и сформулирован алгоритм вычислений. Для разных моделей конкретный ход вычислений будет различным, так что данный блок придется программировать индивидуально. Зато, когда он будет готов, процесс моделирования будет происходить достаточно похожим образом: по указанным формулам будут производиться вычисления (одиночные с некоторым фиксированным значением параметра задачи или серия вычислений, когда параметр автоматически перебирается), а их результаты будут представляться в виде таблиц и графиков. Последние операции по своей сути слабо зависят от характера представляемой информации, так что имеет смысл реализовать их универсальным образом. Опыт разработки материалов практикума показал, что желательно предусмотреть таблицы и графики двух типов — для представления текущих результатов по каждому отдельному расчету и обобщающих данных по результатам совокупности расчетов. Например, в задаче о резонансе каждый расчет представляет собой проведение виртуального эксперимента по наблюдению картины воздействия на колебательную систему с фиксированной частотой, а обобщающим графиком, построенным по результатам серии расчетов с различными частотами, будет резонансная кривая зависимости от частоты максимального отклонения системы от положения равновесия. Таким образом, типичная программа нашего практикума будет содержать следующие основные модули: · основной вычислительный модуль; · модуль рисования графиков для каждого расчета; · модуль рисования обобщающего графика; · модуль построения таблицы значений по каждому отдельному расчету; · модуль построения обобщающей таблицы. Важно подчеркнуть, что четыре последних пункта списка являются универсальными и не зависят от конкретной задачи. Общая структура практикума представлена на рис. 3.13.
Выбранная структура потребует определенного структурирования файлов проекта. Удобно каждый проект помещать в отдельную папку, а для общей части проекта создадим папку common.
Рис. 3.14 На приведенном рисунке подготовлены папки для двух проектов (“Спутник” и “Радиоактивный распад”), обсуждавшаяся выше общая папка, а также папка для рисунков для управляющих кнопок и иконок (значков) проектов. Приведенная структура папок должна учитываться при сохранении модулей проектов. Примечание. Создание описанной выше структуры пакета может на первый взгляд показаться излишним. Существует простой альтернативный вариант — работать с каждым проектом отдельно, копируя во все папки общие файлы. Недостаток такого подхода состоит не столько в том, что напрасно продублированные общие файлы занимают место на диске; гораздо важнее, что неудобно вносить исправления в организованные таким образом проекты. В самом деле, представьте, что вы сделали незначительное исправление в модуле построения графиков. Тогда вам придется “растиражировать” исправленный модуль во все папки, загрузить каждый проект и его перекомпилировать. В то же время, при использовании описанной нами методики достаточно после указанного исправления модуля выбрать в меню пункт перекомпиляции всех проектов — и Delphi автоматически перекомпилирует сразу все проекты. Итак, мы подготовили необходимую структуру каталогов. Теперь остается создать связанные между собой проекты, используя предусмотренный для этой цели в Delphi специальный механизм project group (группы проектов). Учитывая, что данная возможность среды в учебной литературе обычно не раскрывается, расскажем подробнее, как с ним работать. Рассмотрение будем вести на слегка упрощенном примере: объединим всего два проекта. Запустим Delphi, и система обычным образом создаст одиночный проект, правда, предусмотрительно заготовив для него файл с проектной группой (иными словами, если не предпринимать специальных действий, то проектная группа получит стандартное имя ProjectGroup1 и будет состоять из единственного проекта; из сказанного понятно, почему на ней в простейших упражнениях не фиксируют внимания). Сначала сохраним проект в соответствии с разработанной нами структурой. Для этого выберем в меню пункт Save project as… и очень внимательно поработаем с диалогами сохранения файлов. Первый модуль, который является главным в данном проекте (для определенности “Спутник”), сохраним в индивидуальную папку:
Рис. 3.15 Наиболее важные места диалога, на которые надо обязательно обратить внимание, на рис. 3.15 выделены. В частности, видно, что первый модуль сохраняется в папку sputnik. Подчеркнем, что для простоты имя модуля unit1, данное Delphi, можно оставить без изменения. Модуль unit2 (а также все последующие) сохраним в другую папку — common. Еще раз напомним читателям, что данная папка предусмотрена для хранения общей части проектов.
Рис. 3.16 Наконец, сохраним файл проекта, не забыв при этом дать ему нужное нам название sputnik (это стоит сделать, поскольку имя проекта присваивается скомпилированному exe-файлу).
Рис. 3.17 Не забудьте, что файл проекта должен находиться в индивидуальной папке sputnik, а не в common! Теперь, когда наш проект надежно сохранен, позаботимся о проектной группе. Вызовем окно управления проектом (Project Manager), воспользовавшись первым пунктом в меню view. Оно будет выглядеть примерно так, как показано на рис. 3.18 (обязательно обратите внимание на правильность каталогов в правой части окна!).
Рис. 3.18 Остается переименовать стандартную ProjectGroup1, например, в praktikum, щелкнув по ней правой кнопкой и выбрав в появившемся меню Save Project Group As…
Рис. 3.19 Подчеркнем, что данный файл, который объединяет все проекты, целесообразно разместить на самом верхнем уровне иерархии папок нашего практикума. Теперь займемся вторым проектом. Снова запустим Delphi и подготовим второй проект. Его главный (уникальный для проекта) модуль unit1 сохраним описанным выше способом в папку radioactiv. А вот с остальными модулями придется действовать по-другому, так как они уже сохранены в общей части. Их надо подключить к проекту, воспользовавшись первым пунктом меню Project, который называется Add to Project (добавить к проекту).
Рис. 3.20 Формирование очередного проекта завершено. Остается присоединить его к нашему практикуму. Для этого щелкнем по значку файла praktikum.bpg, который был создан ранее, и в меню Project или окне Project Manager выберем действие Add Existing Project … (добавить существующий проект).
Рис. 3.21 В итоге в нашу группу войдет уже два проекта, а Project Manager примет вид:
Рис. 3.22 Аналогичным способом можно собрать в единое целое и все остальные проекты моделирования физических задач. В частности, окончательный состав проекта выглядел на нашем компьютере весьма впечатляюще (два первых проекта для наглядности “раскрыты”) (см. рис. 3.23).
Рис. 3.23 Примечание. Delphi допускает создание нового проекта, “не выходя” из проектной группы, т.е. проект radioactiv можно было бы создавать, находясь непосредственно в praktikum. Эта процедура немного проще, чем та, которая была описана выше, но в этом случае нумерация форм нового проекта продолжает имеющуюся (например, первая форма получает имя Form6). Еще раз подчеркнем, что описанная нами процедура создания единого проекта есть не стремление “оригинальничать”, а вполне оправданный с точки зрения практического удобства подход. Именно в таком виде публикуемый пакет оказывается максимально открытым для расширения, позволяя творческим учителям легко дополнить его новыми физическими моделями. Устройство типичного проекта Теперь, когда стали понятны общие идеи построения программного обеспечения практикума, рассмотрим отдельно взятый проект моделирования одной из физических задач. В качестве такового выберем проект “Спутник”, включающий в себя все пять перечисленных в предыдущем разделе модулей. Большинство проектов практикума устроены совершенно аналогично, но есть и исключения: проект “Радиоактивный распад” в силу простоты своей математической постановки “обходится” всего тремя модулями. “Спутник”, как и любое Windows-приложение, будет состоять из окон. Для наших целей естественным образом напрашивается создание пяти окон: · главного с основными органами управления процессом численного моделирования (с ним ассоциируется программа вычислений для конкретной модели), · двух окон построения графиков: для каждого расчета и итогового · и двух окон с таблицами наиболее важных физических характеристик: в первое помещаются интегральные характеристики процесса в целом, а во второе — промежуточные числовые результаты расчетов по каждому из графиков. Возможный вид реализации виртуальной лабораторной среды приведен на рис. 3.24. Рассмотрим теперь подробнее программы на Паскале, ассоциированные с каждым из окон приложения.
Рис. 3.24 Модуль 1. Main Начнем с главного окна, обеспечивающего основной пользовательский интерфейс, а также определяющего ход вычислений для модели “Спутник”. Если пропустить стандартную “шапку” описаний, которую Delphi генерирует автоматически, программа открывается блоком параметров, приспосабливающим универсальные общие модули к конкретной исследуемой модели. Поскольку эти параметры предназначены для остальных модулей, данное описание размещено в интерфейсной части главного модуля. {Блок параметров} const Nparam = 5; {число параметров в таблице} tabTitles: array [0..4] of string[2] = ('V0','e','T','a','k3'); tab2Tit='V0 \ t='; NZ1=6; NZ2=3; {десятичные знаки в таблице} neopred=-1000;{значение не определено и не отобразится в таблице} myScreenX=520; myScreenY=(3*myScreenX) div 4; {размеры графич. поля} Narg=0; Nfunc=2; {номера столбцов, по которым строится итоговый график} В открывающейся далее реализационной части основную часть занимает программа вычислений, имеющая для проекта “Спутник” следующий вид. var x,y,Vy,Vx,t,tp,a,v0,e,k3,dt:double; {физические величины} mnogo,myStop:boolean; {для регулир. количества графиков и останова} {ускорение} function ax(x,y,t:real):double; begin ax:=-x/(sqrt(x*x+y*y)*(x*x+y*y));end; function ay(x,y,t:real):double; begin ay:=-y/(sqrt(x*x+y*y)*(x*x+y*y));end; {начальные условия} procedure nachsost(Vnach:double); begin t:=0;x:=1;y:=0;Vx:=0;V0:=Vnach;Vy:=V0 end; {один шаг расчета и вызов визуализации} procedure trace; begin vx:=vx+ax(x,y,t)*dt; x:=x+vx*dt; vy:=vy+ay(x,y,t)*dt; y:=y+vy*dt; grPutPixel(x,y); end; {интегральные параметры траектории} procedure integr; begin param[1]:=e; param[2]:=tp; param[3]:=a; param[4]:=k3; tabLine; {сформировать строку в таблице} end; procedure buttons(b:boolean); begin {активация кнопок "Счет" и "Стоп" ("в противофазе")} with Form1 do begin BitBtn3.Enabled:=b; {"Стоп"} Button1.Enabled:=not b; {"Счет" - 1 график} Button2.Enabled:=not b; {"Счет" - много графиков} end; end; procedure graphic1(mnogo:boolean); var v1,v2,v3,vh,s,Xmin,Ymax,yold,xold,Tprint,tpr:double; i,n:integer; begin if mnogo then {много графиков} begin v2:=StrToFloat(Form1.Edit2.Text); {начало} v3:=StrToFloat(Form1.Edit3.Text); {конец} n:=Form1.ComboBox1.ItemIndex+2;{число траект.} vh:=(v3-v2)/(n-1);{шаг} v0:=v2;{нач. скорость} end else {1 график} begin v1:=StrToFloat(Form1.Edit1.Text); v0:=v1;{нач. скорость} n:=1;{1 траект.} vh:=0{шаг} end; Xmin:=StrToFloat(Form1.Edit4.Text);{левая граница графиков} Ymax:=StrToFloat(Form1.Edit7.Text);{верхняя граница графиков} dt:=StrToFloat(Form1.Edit8.Text); {шаг по времени} Tprint:=StrToFloat(form4.edit2.Text); myStop:=false; buttons(true); {активация кнопки "Стоп"} i:=1; {номер траектории} repeat {n траекторий} if v0<>0 then {V0=0 - не считает} begin ClearLastPoint; {сбросить коорд. последней точки} nachsost(v0);{начальные условия} e:=0; {T, a и K3 пока не определены} tp:=neopred; a:=neopred; k3:=neopred; tpr:=Tprint; s:=0; param[0]:=V0; repeat {расчет траектории} xold:=x;yold:=y;{запомнить коорд. пред. точки} t:=t+dt; trace; {шаг и визуализация} s:=s+(x*vy-y*vx); {площадь сектора} if (t>=tpr) then begin s:=0.5*s*dt; tpr:=tpr+Tprint; tab2AddValue(s); s:=0 end; if (xold>0)and(x<=0) then e:=abs(y-1); if (yold>=0)and(y<0)then {определить T, a и K3} begin tp:=2*t;a:=(1-x)/2; k3:=tp*tp/(a*a*a); end; {пауза для рисования} Application.ProcessMessages; until (((yold<0)and(y>0)){закончен оборот} or (((x<Xmin)or(y>Ymax))and(e>1))) {выход за пределы поля графика} or myStop; {нажата кнопка "Стоп"} integr; {интегральные параметры траектории} tab2NextLine; end; {if v0<>0} v0:=v0+vh; i:=i+1; {к следующей траектории} until (i>n) or myStop; {выход когда все траект. или по кнопке} buttons(false); {вернуть кнопки "Счет" и "Стоп" в исходное сост.} end; Ядром вычислительной части программы является процедура Graphic1. При значении параметра mnogo=false она рисует один график, а в противоположном случае — много, считывая начальное и конечное значения с соответствующих полей редактирования главного окна, а количество траекторий — из выпадающего списка. Аналогичным образом, с использованием стандартной функции Delphi под названием StrToFloat (строку в число с плавающей запятой), считывается шаг по времени. Далее следуют вычисления, организованные в виде двух вложенных циклов: внешний обеспечивает вычисление n траекторий (для одиночного расчета полагается n = 1), а внутренний — движение по каждой из траекторий с течением времени. Рабочие формулы и некоторые физические идеи, на базе которых построены вычисления, будут приведены позднее при обсуждении соответствующей модели. Здесь упомянем лишь несколько общих, не связанных с конкретной постановкой, деталей. Специальная процедура buttons служит для активизации кнопки остановки и отключения кнопок запуска при старте вычислений и изменении их состояния на противоположное после их завершения. При этом окончание вычислений данной траектории может происходить по целому ряду причин: совершен полный оборот и траектория замкнулась; разомкнутая траектория вышла за пределы графика или была нажата кнопка “Стоп” (в последнем случае логическая переменная myStop установлена в true). В программе предусмотрено специальное “неопределенное” значение, которое позволяет оставлять пустые клетки в таблице, если данный параметр лишен физического смысла. Например, траектории спутника могут быть замкнутыми и разомкнутыми; в последнем случае параметр “период обращения” как раз и является неопределенным. Взаимодействие главного модуля с графическими и табличными производится через интерфейсные процедуры последних. Например, во внутреннем цикле вызывается процедура tab2AddValue, а после него tab2NextLine, что обеспечивает заполнение табл. 2 с промежуточными результатами расчетов. Внутри процедуры integr (сохранение интегральных параметров), также вызываемой после окончания внутреннего цикла, есть обращение к другому табличному модулю — tabLine (обратите внимание на префиксы — начальные буквы — имен). Для передачи интегральных параметров в табл. 1 предусмотрен специальный интерфейсный массив param. Рисование отдельных точек графика инициируется из процедуры trace, которая, в свою очередь, вызывает стандартную процедуру графического модуля grPutPixel. Что касается построения итогового графика, то этот модуль относительно автономен и запускается нажатием на кнопку, находящуюся на его собственной форме; данные при этом берутся из столбцов табл. 1, номера которых заданы константами Narg и Nfunc. Работа перечисленных выше графических и табличных процедур, а также их устройство заслуживают отдельного обсуждения, которое будет приведено позднее. Кроме описанного выше значительного фрагмента, реализующего вычисления траекторий спутника, в главном модуле имеется также несколько важных вспомогательных процедур, обеспечивающих управление проектом. В частности, приведенный ниже фрагмент демонстрирует запуск расчетов (одиночного или для нескольких траекторий) и их прерывание по желанию пользователя при помощи кнопок Счет-1, Счет-М и Стоп. procedure ShowWin; begin form3.show; {показать окно с таблицей 1} form2.show; {показать окно с графиками} grSetSize(myScreenX,myScreenY); {установить размеры граф. поля} form4.show; {показать окно с таблицей 2} form5.show; {показать окно с итоговым графиком} Form1.SetFocus; {вернуть фокус на главное окно} end; procedure TForm1.Button1Click(Sender: TObject); begin ShowWin; {показать окна} mnogo:=false; graphic1(mnogo); {рисовать 1 график} end; procedure TForm1.Button2Click(Sender: TObject); begin ShowWin; {показать окна} mnogo:=true; graphic1(mnogo); {рисовать много графиков} end; procedure TForm1.BitBtn3Click(Sender: TObject); {обеспечить досрочный выход из цикла расчетов} begin myStop:=true end; К ним добавляются короткие обработчики кнопок очистки таблиц и графиков, а также программа поддержки выпадающего списка установки цвета графиков, приведенные ниже. procedure TForm1.BitBtn1Click(Sender: TObject); begin tabClearVal; {очистка значений таблицы 1} tab2ClearVal end; procedure TForm1.BitBtn2Click(Sender: TObject); begin {очистка графиков} with form2.Image1 do Canvas.FillRect(Rect(0,0,width,height)); end; procedure TForm1.grColorChange(Sender: TObject); begin {выбор цвета графиков} case grColor.ItemIndex of 0:grCurColor:=clBlack; 1:grCurColor:=clMaroon; 2:grCurColor:=clGreen; 3:grCurColor:=clOlive; 4:grCurColor:=clNavy; 5:grCurColor:=clPurple; 6:grCurColor:=clTeal; 7:grCurColor:=clGray; 8:grCurColor:=clSilver; 9:grCurColor:=clRed; 10:grCurColor:=clLime; 11:grCurColor:=clYellow; 12:grCurColor:=clBlue; 13:grCurColor:=clFuchsia; 14:grCurColor:=clAqua; 15:grCurColor:=clWhite; end;{case} Shape1.Brush.Color:=grCurColor; end; Наконец, последняя процедура инициализирует компоненты формы при старте программы: производится автоматическое центрирование формы в зависимости от размеров экрана, устанавливается черный цвет рисования графиков и число графиков, равное двум. Разумеется, данные значения в дальнейшем пользователь волен изменить по своему усмотрению. procedure TForm1.FormCreate(Sender: TObject); begin with Form1 do {центровка главной формы} begin top:=0; left:=(screen.Width-width) div 2; end; grColor.ItemIndex:=0; Shape1.Brush.Color:=clBlack; {выбор цвета} combobox1.ItemIndex:=0; {число графиков} end; Модуль 2. Graph Модуль предназначен для рисования графиков каждого из расчетов. В его состав входят следующие процедуры, важнейшей из которых, без сомнения, является grPutPixel.
Некоторые из указанных в таблице процедур в проекте “Спутник” не требуются; например, функция centr_krug предназначается для проекта “Опыт Резерфорда”, а grLine — для проекта “Броуновское движение”. Поскольку принципы рисования графиков были подробно описаны ранее, приведем полный текст программ без описания. Надеемся, что имеющихся в программе подробных комментариев будет достаточно для понимания. var Form2: TForm2; grCurColor: TColor; procedure grSetSize(x,y: integer); procedure centr_krug; procedure grPutPixel(x,y: double); procedure grPutPoint(x,y: double); procedure grLine(x1,y1,x2,y2: double); procedure ClearLastPoint; implementation uses main, tabl1; {$R *.DFM} var Mx,My,X0,Y0:double; {масштаб, границы граф. области} Ymax, LastPointX,LastPointY:integer; procedure grSetSize(x,y: integer); {установить размеры графической области} var dx,dy:double; xa,ya:integer; begin Form2.ClientWidth:=x; Form2.ClientHeight:=y; {размеры} {установить окно у левой границы экрана} form2.left:=screen.Width-Form2.Width; Ymax:=y; {считать коорд. границ и рассчитать размеры граф. области} X0:=StrToFloat(Form1.Edit4.Text); Y0:=StrToFloat(Form1.Edit6.Text); dx:=StrToFloat(Form1.Edit5.Text)-X0; dy:=StrToFloat(Form1.Edit7.Text)-Y0; Mx:=x/dx; My:=y/dy; {масштаб: пикселей/ед.длины} with Form2.Image1.Canvas do {рисуем оси} begin xa:=round(y+y0*My); MoveTo(0,xa); LineTo(x,xa); {X} ya:=round(-x0*Mx); MoveTo(ya,0); LineTo(ya,y); {Y} end; end; procedure centr_krug; {рисует единичный круг в центре} begin Form2.Image1.Canvas.Ellipse(round((-1-X0)*Mx),Ymax-round((1-Y0)*My),round((1-X0)*Mx), Ymax-round((-1-Y0)*My)); end; procedure grPutPixel(x,y: double); var xp,yp:integer; begin xp:=round((x-X0)*Mx); yp:=Ymax-round((y-Y0)*My); {в пикселях} {новая точка не совпадает с последней нарисованной?} if (LastPointX=xp) and (LastPointY=yp) then exit; {проверка попадания точки в граф. область} if (xp<0) or (xp>Form2.Image1.Width) then exit; if (yp<0) or (yp>Form2.Image1.Height) then exit; {запомним координаты новой точки} LastPointX:=xp; LastPointY:=yp; {нанесем точку на график} Form2.Image1.Canvas.Pixels[xp,yp]:=grCurColor; end; procedure grPutPoint(x,y: double); const r=2; var xp,yp:integer; begin xp:=round((x-X0)*Mx); yp:=Ymax-round((y-Y0)*My); {в пикселях} {нанесем кружок на график} Form2.Image1.Canvas.Pen.Color:=grCurColor; {цвет} Form2.Image1.Canvas.Ellipse(xp-r,yp+r,xp+r,yp-r) end; procedure grLine(x1,y1,x2,y2: double); var xp,yp:integer; begin xp:=round((x1-X0)*Mx); yp:=Ymax-round((y1-Y0)*My); {в пикселях} Form2.Image1.Canvas.MoveTo(xp,yp); xp:=round((x2-X0)*Mx); yp:=Ymax-round((y2-Y0)*My); {в пикселях} Form2.Image1.Canvas.LineTo(xp,yp) end; procedure ClearLastPoint; {сброс координат последней нарисованной точки (-1 не бывает!)} begin LastPointX:=-1; LastPointY:=-1; end; procedure TForm2.FormCreate(Sender: TObject); {расположим форму под главной} begin top:=form1.top+form1.height; end; initialization ClearLastPoint{сброс координат последней нарисованной точки} end. Форма модуля Form2 не несет на себе никаких органов управления. Модуль 3. Tabl1 Модуль работы с табл. 1, в которую после каждого расчета заносится строка со значениями некоторых интегральных параметров, определяет в своем интерфейсе всего три процедуры без параметров.
Количество столбцов в таблице, их заголовки, а также формат чисел (например, количество знаков после запятой) берутся из констант, определенных в модуле Main. Заметим, что ширина таблицы и затем ширина формы Form3 настраиваются при создании последней следующим образом (см. обработчик события FormCreate). Вызывается процедура tabInit, задающая число необходимых колонок в таблице. Далее, используя количество колонок, хранящееся в свойстве ColCount, рассчитывается ширина таблицы, а по ней и всей формы. var Form3: TForm3; param: array [0..9] of double; procedure tabInit; procedure tabLine; procedure tabClearVal; implementation uses main, graph; {$R *.DFM} procedure tabInit; {инициализируем таблицу} var i:integer; begin with Form3.StringGrid1 do begin colCount:=Nparam; {установим число столбцов} rowCount:=2; {заголовок и одна пустая строка} {перенесем названия параметров в заголовок таблицы} for i:=0 to Nparam-1 do Cells[i,0]:=tabTitles[i]; end; end; procedure tabLine; {заполним строку таблицы} var i,k:integer; s:string[10]; begin With Form3.StringGrid1 do begin k:=RowCount-1; {номер заполняемой строки} RowCount:=RowCount+1; {добавим новую пустую} for i:=0 to Nparam-1 do begin if param[i]=neopred then s:=''{оставить клетку пустой} else str(param[i]:NZ1:NZ2,s); Cells[i,k]:=s; {значения} Cells[i,k+1]:='';{чистим след. строку} end; end end; procedure tabClearVal; {очистим значения в таблице} var i:integer; begin with Form3.StringGrid1 do begin RowCount:=2; {заголовок и 1 строка} for i:=0 to Nparam-1 do Cells[i,1]:='';{очистка} end end; procedure TForm3.FormCreate(Sender: TObject); begin {расположим форму под главной} top:=form1.top+form1.height; tabInit; {инициализируем таблицу} with stringGrid1 do Width:=ColCount*DefaultColWidth+24; width:=stringGrid1.Width+16; end; Форма модуля Form3 не несет на себе никаких органов управления. Модуль 4. Tabl2 Данный модуль обслуживает табл. 2, в которую заносятся результаты расчетов некоторой физической величины для каждой из траекторий (для проекта “Спутник” это секториальная скорость). При формировании табл. 2 используется следующая логика. Каждому расчету соответствует своя строка в таблице. Через заданный пользователем промежуток времени результат заносится в очередную клеточку таблицы. Число столбцов ограничено (задается пользователем), так что чаще всего клетки в строке заканчиваются, и заполнение таблицы возобновляется только после перехода к следующей строке. Заметим, что нижнее поле редактирования, в котором задается физический промежуток времени, используется также в модуле main для обеспечения правильности заполнения таблицы. Для работы с таблицей определены следующие процедуры.
Текст модуля без стандартных сгенерированных системой описаний приводится ниже. procedure tab2NextLine; procedure tab2AddValue(d:double); procedure tab2ClearVal; implementation uses main, tabl1, graph; {$R *.DFM} var curCol:integer; procedure tab2Init; {инициализируем таблицу} var n,i:integer; t:double; s:string; begin with Form4 do begin if edit1.Text='' then exit; n:=StrToInt(edit1.Text); if n<2 then exit; stringGrid1.ColCount:=n+1; for i:=1 to n do {"шапка" таблицы 2} begin t:=StrToFloat(edit2.Text)*(i-1); str(t:NZ1:NZ2,s); stringGrid1.Cells[i,0]:=s end; stringGrid1.Cells[0,0]:=tab2Tit; tab2ClearVal; curCol:=1; end; end; procedure tab2NextLine; {добавим строку таблицы} var i,k:integer; s:string[10]; begin With Form4.StringGrid1 do begin k:=RowCount-1; {номер заполняемой строки} RowCount:=RowCount+1; {добавим новую пустую} for i:=0 to ColCount+1 do Cells[i,k+1]:='';{чистим след. строку} str(param[0]:NZ1:NZ2,s); Cells[0,k]:=s; end; curCol:=1; end; procedure tab2AddValue(d:double); var s:string; k:integer; begin with form4.StringGrid1 do begin if curCol>ColCount then exit; k:=RowCount-1; {номер заполняемой строки} str(param[0]:NZ1:NZ2,s); Cells[0,k]:=s; str(d:NZ1:NZ2,s); Cells[curCol,k]:=s; curCol:=curCol+1; end end; procedure tab2ClearVal; {очистим значения в таблице} var i:integer; begin with Form4.StringGrid1 do begin RowCount:=2; {заголовок и 1 строка} for i:=0 to ColCount do Cells[i,1]:='';{очистка} end end; procedure TForm4.Edit1Change(Sender: TObject); begin tab2Init end; procedure TForm4.FormCreate(Sender: TObject); begin with Form4 do begin left:=form3.left; width:=screen.Width-left; end; edit1.Left:=screen.Width-edit1.Width-12; edit2.Left:=edit1.Left; label1.Left:=edit1.Left; label2.Left:=edit1.Left; stringGrid1.Width:=edit1.Left-16; tab2Init; {инициализируем таблицу} end; Модуль 5. Rez_graph Модуль обеспечивает построение итогового графика по данным табл. 1. Как уже говорилось ранее, итоговый график строится на базе компонента Chart. Входные данные извлекаются из табл. 1 при помощи вспомогательной функции getNumber (ее описание дано при изложении графической проблемы 7), которая работает как для значений аргумента, так и для функции. Извлекая из таблицы нужную клетку, функция дополнительно производит замену символа десятичной точки, используемого при выводе в таблицу, на запятую, которая используется функцией strToFloat. Построение графика не является автоматическим и инициируется специальной кнопкой BitBtn1 или при изменении значения в выпадающем списке ComboBox1. Последний задает некоторый множитель, влияющий на радиус изображаемой точки (ранее при обсуждении компонента Chart уже отмечалось, что радиус измеряется не в пикселях, а в физических единицах, что затрудняет его автоматический выбор и делает весьма желательной возможность пользовательской коррекции). Учитывая, что модуль rez_graph является почти автономным и не содержит ни одной доступной извне интерфейсной процедуры, таблица процедур в описании данного модуля отсутствует. function getNumber(k,y:integer):double; {извлекает из таблицы 1 значение аргумента (k=0) или функции (k=1) из строки с номером y} var s:string; begin if k=0 then k:=Narg else k:=Nfunc; {аргумент/функция} s:=form3.StringGrid1.Cells[k,y]; {содержимое ячейки} k:=pos('.',s); if k<>0 then s[k]:=','; {замена десятич. '.' на ','} getNumber:=strToFloat(s) {результат - вещественное число} end; procedure TForm5.BitBtn1Click(Sender: TObject); var n:integer; max,min,radius:double; begin if form3.StringGrid1.Cells[Nfunc,1]<>'' {значение не определено} then max:=getNumber(0,1) else max:=0; min:=max; n:=1; while form3.StringGrid1.Cells[Nfunc,n]<>'' do {поиск min и max} begin if min>getNumber(1,n) then min:=getNumber(1,n); if max<getNumber(1,n) then max:=getNumber(1,n); n:=n+1; end; {автоматический выбор радиуса рисования точек} radius:=max-min; if radius=0 then radius:=max; {ручная коррекция - множитель берется из списка} radius:=(comboBox1.ItemIndex+1)*0.005*radius; with series1 do begin ParentChart:=Chart1; {связать Chart1 и Series1} n:=1; clear;{очистка старого графика} while form3.StringGrid1.Cells[Nfunc,n]<>'' do {пока есть числа} begin addBubble(getNumber(0,n),getNumber(1,n),radius, floatToStr(getNumber(0,n)),clRed); n:=n+1 {к следующей строке таблицы 1} end end; end; procedure TForm5.FormCreate(Sender: TObject); begin comboBox1.ItemIndex:=4; end; Таким образом, мы подробно рассмотрели, как устроен проект “Спутник”. Остальные модели устроены аналогично. Те небольшие отличия, которые у них имеются, читатели смогут без труда понять самостоятельно.
4. Реализация моделей физических процессов в среде Microsoft ExcelЧасто электронные таблицы определяют как приложение, которое позволяет производить сложные вычисления без программирования. В действительности это не так, поскольку для вычислений нужно набирать формулы, которые, по сути, представляют собой арифметические или логические выражения. Их структура определяется синтаксическими правилами, подобными правилам языков программирования. Более существенной для моделирования, однако, является реализация вычислительного алгоритма. В электронных таблицах автоматически поддерживается алгоритмическая структура “следование”: сканирование ячеек проводится по возрастанию адресов столбцов и строк. Структура “ветвление” ограничена вычислением альтернативных значений ячейки, где она помещена, и не допускает изменения содержимого другой ячейки или условного перехода по заданному адресу. Циклическая структура стандартными средствами не поддерживается. Поскольку любой динамический процесс является циклическим для моделирования в среде MS Excel, оказывается необходимой организация стандартных средств для реализации циклической алгоритмической структуры. Единственной возможностью такой реализации является представление цикла как структуры “следование”. Это значит, что с помощью электронных таблиц можно реализовать циклы с параметром, при условии, что количество повторений определено. Такие циклы представляются таблицами, в строках которых вычисляются значения характеристик процесса в последовательные моменты времени. Циклы с постусловием или предусловием, которые разворачиваются в структуру “следование” с переменным числом шагов, стандартными средствами не реализуются. Отметим, что мы сознательно не рассматриваем расширение возможностей таблиц, связанное с формированием макросов, которые представляют собой программные модули Visual Basic. Из сказанного следуют важные ограничения на реализацию моделей динамических процессов с помощью электронных таблиц, по сравнению с возможностями среды Delphi. Первое ограничение состоит в том, что имитация динамики процесса невозможна, т.е. зависимость от времени характеристик процесса может быть представлена только “в целом”, в то время как в Delphi эта зависимость формируется по шагам. Второе ограничение состоит в том, что величина временного интервала моделирования в рамках сформированной таблицы может изменяться в ограниченных пределах. Действительно, определение числа строк таблицы означает задание числа шагов по времени. Тогда размер интервала моделирования определяется шагом по времени, для которого существуют ограничения, связанные с устойчивостью вычислительного процесса и погрешностью аппроксимации. Ограниченными оказываются также возможности графического представления изучаемого процесса при различных значениях определяющих параметров, поскольку каждому графику соответствует таблица. Таким образом, для изображения в одних осях нескольких графиков необходимо формирование нескольких таблиц. Тем не менее использование электронных таблиц для реализации математических моделей позволяет увеличить число школьников, привлекаемых к активному знакомству с математическими моделями физических процессов. Перейдем теперь к обсуждению структуры типичного проекта. Общий алгоритм состоит из трех блоков. Первый блок — формирование таблицы значений характеристик процессов в последовательные моменты времени; второй — построение графика с помощью встроенного мастера диаграмм; третий — оформление интерфейса. Первый блок содержит следующие шаги: определение параметров таблицы, определение структуры записи, т.е. данных, которые должны быть расположены в строке таблицы, определение количества записей, заполнение таблицы расчетными формулами и необходимыми значениями. Шаги, образующие второй блок, однозначно определяются мастером диаграмм. Шаги третьего блока определяют удобное для проведения исследований расположение параметров, таблиц значений и графиков зависимостей. Рассмотрим перечисленные шаги более подробно на примере задачи о спутнике. Параметры таблицы В качестве параметров следует выбирать величины, задание которых определяет ее размеры и числовые значения данных, получаемых в ячейках таблицы. Значения параметров не изменяются в процессе вычислений; они размещаются в фиксированных ячейках, при обращении к которым используется абсолютная адресация. В задаче о спутнике, например, значения координат спутника в любой момент времени однозначно определяются начальными условиями, поэтому их естественно определить в качестве параметров. Выбранный метод пошагового решения задачи содержит в качестве основной характеристики шаг по времени dt, который также включается в список параметров. Таким образом, таблицу определяют четыре физических параметра — x0, y0, vx0, vy0 и один вычислительный — dt. Структура записи В ячейках строки таблицы (слева направо) следует расположить момент времени и вычисляемые характеристики моделируемого процесса. Порядок характеристик должен соответствовать соглашениям мастера построения диаграмм, а именно, значения аргумента, которые откладываются на горизонтальной оси диаграммы в таблице, располагаются левее значений функции. Для задачи о спутнике последовательность данных в строке такова: момент времени, проекция скорости на ось x, проекция скорости на ось y, координата x, координата y, мгновенная секториальная скорость, две вспомогательные ячейки. Все данные (кроме секториальной скорости) вычисляются по формулам численного метода, представляющим собой рекуррентные соотношения, с помощью которых значение в данной ячейке определяется значениями величин в предыдущий момент времени, т.е. в предыдущей строке. Вспомогательные ячейки используются для выделения значений координат x и y, которые определяют такие параметры траектории, как эксцентриситет и большая полуось. Количество записей Размер таблицы определяется величиной шага по времени и количеством шагов по времени, которые мы должны указать до решения задачи, хотя необходимое число шагов определяется в процессе решения каким-либо условием: замыкания траектории для задачи о спутнике, завершения процесса распада в задаче о радиоактивности и т.д. Шаг по времени определяется устойчивостью вычислительной процедуры и точностью решения. Обойти эту трудность можно посредством процедуры типа предиктор-корректор, изменяя количество записей, т.е. переделывая таблицу для каждого расчетного варианта, либо создавая таблицу для некоторого “среднего” варианта, чтобы затем обследовать варианты, соответствующие другим характерным временам путем изменения только шага по времени с сохранением устойчивости счета и разумной точности решения. В задаче о спутнике таким “средним” вариантом является движение по круговой траектории, радиус которой равен 1 в выбранных единицах измерения расстояния. Скорость движения также равна 1, поэтому время одного полного оборота 6,28 единиц. Выбирая шаг по времени равным 0,001, находим, что таблица будет содержать 6280 записей. Увеличение шага по времени при сохранении количества записей увеличивает время моделирования, и мы получаем возможность рассмотреть эллиптические и иные траектории. Заполнение таблицы Для заполнения таблицы нужно
сформировать две строки. В первой строке
соответствующим величинам передаются начальные
значения. Вторая строка содержит вычислительные
формулы, в которых значения величин берутся из
ячеек первой строки, а параметры варианта — из
интерфейсной части проекта. Для ссылок на эти
ячейки таблицы используется относительная
адресация. Для ссылок на параметры — абсолютная.
Заполнение оставшихся строк таблицы
производится простым копированием второй
строки. Поскольку число строк может быть очень
большим (в задаче о спутнике — несколько тысяч),
использование приема “растягивание”
оказывается неэффективным. Следует использовать
прием предварительного копирования в clipboard и
последующей вставки в выделенный диапазон ячеек.
Выделение нужного диапазона удобно проводить с
помощью перехода при нажатой клавише Построение графика зависимости Для построения графика зависимости рекомендуется использовать диаграмму точечного типа, сглаженную, без координатных точек. Поскольку масштаб диаграммы по умолчанию определяется автоматически, визуальный контроль изменения значений характеристик процесса при изменении параметров затруднен. Поэтому рекомендуется после ряда экспериментов фиксировать границы изменения характеристик по осям диаграммы. Правильные пропорции зависимости можно получить обычным масштабированием диаграммы. Так, для задачи о спутнике следует определить оси системы координат одинакового размера с одинаковыми максимальными и минимальными значениями. Для увеличения полезной площади диаграммы легенду рекомендуется удалить. Организация интерфейса Для более удобной работы предлагается собственно таблицу и начальные данные с графиком траектории разместить на разных листах Книги MS Excel. Предлагаемый образец размещения данных выглядит следующим образом.
5. Движение в центральном поле тяготенияПостановка задачи Задача о движении тела в центральном поле тяготения является хорошим примером, демонстрирующим возможности использования ПК для изучения поведения объекта, подчиняющегося некоторым общим физическим законам. Процесс выведения спутника на орбиту обычно разбивается на два этапа. На первом этапе спутник поднимается над атмосферой практически вертикально на некоторую высоту. Затем обычно последняя ступень ракетоносителя придает спутнику необходимую горизонтальную скорость, и далее он двигается по инерции. Рассмотрим инерционный полет небольшого тела (спутника) около притягивающего центра с большой массой (Земли). Будем интересоваться тем, какие траектории спутника возможны, какой должна быть его минимальная скорость вблизи поверхности Земли, чтобы он, двигаясь по круговой траектории, не упал на Землю (первая космическая скорость), какой должна быть минимальная начальная скорость спутника, чтобы получилась незамкнутая траектория и спутник ушел от Земли (вторая космическая скорость). В численном эксперименте можно также проверить законы Кеплера: 1) притягивающий центр расположен в одном из фокусов орбиты; 2) радиус-вектор от Солнца до планеты “заметает” равные площади за равные промежутки времени; 3) квадраты периодов обращения спутников вокруг притягивающего центра относятся как кубы больших полуосей эллипсов их орбит. В основу модели мы положим закон всемирного тяготения. Будем считать, что на тело, движение которого рассматривается, действует только сила тяготения и уравнение Ньютона имеет вид:
Здесь m и M — масса спутника и масса притягивающего центра, G — гравитационная постоянная, r — радиус-вектор, задающий положение спутника относительно притягивающего центра, a — ускорение спутника. Заметим, что хотя закон всемирного тяготения в форме (1) записан для материальных точек, он имеет такую же форму для сферически-симметричных тел. Движение тела под влиянием центральной силы происходит в одной плоскости, положение которой определяется векторами r0 и v0, задающими начальное положение тела и его начальную скорость. Декартову систему координат с началом в центре тяготения и начало отсчета времени выберем так, чтобы движение происходило в плоскости Oxy и в начальный момент скорость тела была перпендикулярна оси x (рис. 5.1).
Рис. 5.1. Система координат и возможная траектория спутника Тогда начальные условия можно записать в виде: t = 0: x = x0, y = 0, vx = 0, vy = v0. (5.2) Уравнение (1) вместе с условиями (2) полностью определяют траекторию спутника и все ее свойства. Численная модель Численный анализ задачи удобно
проводить, используя в качестве единиц измерения
характерные масштабы задачи. В качестве единицы
длины удобно взять x0. Если разговор
идет о спутнике Земли, то эта величина имеет
порядок радиуса Земли R и равняется R + h,
где h — высота спутника над поверхностью
Земли. Всякое расстояние теперь будет
задаваться числом, которое показывает, сколько
раз в нем укладывается x0. Безразмерное х
будет равняться х, измеренному в метрах,
деленному на х0, также измеренному в метрах.
Единицу времени удобно построить, используя
гравитационную постоянную и характеристики
притягивающего центра. Из уравнения (1) легко
видеть, что множитель GM/r2 имеет
размерность ускорения (м/с2). Вместо
расстояния r возьмем x0 и сформируем
выражение с размерностью времени (с): Измеренные в этих единицах проекции ускорения определяются следующими уравнениями (здесь и далее для безразмерных физических величин использованы те же обозначения, какие использовались для соответствующих размерных величин):
Все физические величины измеряются теперь в относительных единицах и будут одинаковыми для всех систем “спутник — притягивающий центр”. Уменьшилось также число параметров задачи. Единственный безразмерный параметр V0, который остался в задаче, показывает, как соотносятся между собой кинетическая и потенциальная энергии спутника в начальный момент. Действительно, кинетическая энергия спутника в начальный момент равна K = мv02/2, потенциальная энергия для ньютоновского закона тяготения равна П = GMm/x0, и V02 = 2K/П. Для нахождения в различные моменты
времени проекций скорости спутника и его
координат на временной оси выберем дискретные
точки tn, отстоящие друг от друга на
малые интервалы а координаты в этот момент будем
вычислять, как при равномерном движении (опять
считая, что интервал времени
В начальный момент времени проекции скорости и координаты спутника известны:
Система (5)–(8) позволяет шаг за шагом,
при малом Для классификации траекторий удобно
вычислять их эксцентриситет е. В выбранной
системе координат для вычисления
эксцентриситета необходимо определить
координату y = p точки на траектории, для
которой . Тогда e = |p-1|. Если е < 1, то
траекторией является замкнутая кривая
(окружность при е = 0 и эллипс при e Площадь, “заметаемую”
радиус-вектором за некоторое время
Интересно сравнить эти площади, вычисленные на разных участках траектории. По второму закону Кеплера они должны быть равны. По третьему закону Кеплера квадраты
периодов обращения относятся как кубы больших
полуосей орбит, т.е. для каждой траектории
величина Моделирование задачи в среде Delphi Экспериментальное изучение предлагаемых физических проблем средствами описанной выше системы имеет много общего, поэтому в первой задаче мы подробно опишем работу в виртуальной лабораторной среде. Возможный вид реализации этой среды приведен на рис. 5.2. Поскольку подавляющее большинство органов управления сосредоточено в главном окне, имеет смысл обратить основное внимание на его рассмотрение. Из приведенного рисунка устройство главного окна видно вполне отчетливо.
Рис.5.2. Возможный вид виртуальной лабораторной среды В левой части рассматриваемого окна располагается панель с 4 полями ввода, используя которые можно регулировать отображаемую в графическом окне область. Рядом со схематическим прямоугольником графического экрана предусмотрены поля для ввода минимального и максимального значений по каждой из осей X и Y. Отметим, что координаты, как и все остальные вводимые в главном окне параметры, указываются непосредственно в “физических” единицах; необходимый для рисования перевод в пиксели экрана берет на себя программа. Следующая панель, занимающая основную
часть главного окна в его центре, служит для
задания параметров задачи — скорости запуска
спутника V0 и шага по времени dt (Dt —
в постановке задачи), В правой части главного окна есть еще три полезных органа управления: выпадающий список для выбора цвета рисования последующих траекторий и две кнопки очистки графического окна и значений в таблицах (они различаются по нанесенным на них пиктограммам). Все кнопки активны в процессе работы программы. Таким образом, описанные выше органы управления позволяют провести полное исследование физической модели спутника. Можно пробовать рисовать различные траектории и стирать их, подбирая именно те значения параметра, которые требуется найти в соответствии с целью исследования, в частности, в соответствии с поставленным учителем заданием. Окна с графиками функций и табл. 1 интегральных результатов для каждой траектории никаких органов управления не содержат. Зато для построения табл. 2 в правой части окна помещены два поля для ввода параметров построения данной таблицы. В первое вводится количество столбцов табл. 2, которое с точки зрения физического содержания задачи равняется числу точек траектории, для которых будет зафиксировано значение некоторой интересующей нас характеристики (в данной задаче это площадь сектора). Что касается второго поля, то в него задается значение времени, через которое эти значения будут заноситься в таблицу. Например, при указанных на рисунке значениях в таблицу для каждой траектории попадет по 10 точек для значений времени 0,1, 0,2, …, 1. В окне “Итоговый график” по двум колонкам табл. 1 “пузырьками” можно построить график функции. Номера колонок указаны в основном модуле программы. Построение графика осуществляется нажатием кнопки “Построить”. Другой кнопкой этого окна регулируется размер “пузырьков”. Обе кнопки активны в процессе всей работы программы. Эксперимент на модели в среде Delphi Проведем экспериментальное исследование движения спутника с помощью описанной выше модели. Для проведения численного эксперимента нужно прежде всего выбрать шаг по времени dt, с которым будем строить траекторию. По смыслу метода он должен быть достаточно малым, чтобы на этом интервале можно было пренебречь изменением ускорения при вычислении скорости и изменением скорости при вычислении новых координат. Шаг не должен быть и слишком маленьким, так как в этом случае для построения траектории потребуется большое время. Поскольку в качестве масштабов мы выбрали характерные параметры системы, то типичный временной интервал жизни системы равен 1. Малый интервал dt поэтому должен быть много меньше единицы; выберем его, например, равным 0,01. Второй параметр, который нужно задать, это начальная скорость. Опять, пользуясь тем, что расчет ведется в собственных масштабах задачи, для первого эксперимента естественно положить V0 = 1. Теперь можно построить одну траекторию, нажав кнопку “Счет-1”. Посмотрим на полученную траекторию. Она похожа на окружность, но не замкнулась при обороте спутника вокруг притягивающего центра (внутренняя кривая на графиках рис. 5.3). Это, по-видимому, связано с недостаточной точностью счета. Давайте уменьшим величину dt в два раза: dt = 0,005 и изменим цвет кривой. Экран и таблицы чистить не будем, чтобы сравнить результаты, полученные для разных dt. Нажимаем кнопку “Счет-1”. Результат лучше, но требуется еще более мелкий шаг. Сделаем dt = 0,001.
Рис.5.3. Состояние окон с результатами после эксперимента по выбору dt Траектория получилась замкнутая. Если
мы теперь посмотрим на интегральные
характеристики построенных кривых (табл. 1 на рис. 5.3),
то заметим, что эксцентриситет е с
увеличением точности счета уменьшался и
приблизился к нулю. Может быть, не ноль, потому
что еще грубо считаем? Уменьшим dt до 0,0001. Новый
цвет кривой и кнопка “Счет-1”. (На рис. 5.3
приведено состояние окон после проведенных
расчетов.) Вот теперь хорошо! Эксцентриситет
равен нулю, большая полуось равна единице —
значит, траектория окружность. Первая
космическая скорость в принятых единицах равна 1,
а период обращения — Теперь можно посмотреть, какие еще бывают траектории спутника. Построим серию траекторий из 11 линий с диапазоном начальных скоростей от 1 до 2. Очистим графическое поле и таблицу, наберем необходимые параметры и кнопкой “Счет-М” запускаем программу. На рис. 5.4 приведены результаты этого эксперимента. Видно, что с увеличением начальной скорости эллипсы вытягиваются вдоль оси х. Притягивающий центр (начало координат) находится в правом фокусе эллипсов. Последняя замкнутая траектория получилась для V0 = 1,4 (она так сильно вытянута, что не поместилась на экране). Для этой траектории эксцентриситет близок 1, а значит, соответствующая ей начальная скорость близка ко второй космической скорости. Анализ данных таблиц показывает, что второй и третий законы Кеплера хорошо выполняются.
Рис.5.4. Состояние окон с результатами после расчета серии траекторий Эксперимент на модели в среде MS Excel Расположим интерфейсную часть модели, т.е. параметры, диаграмму и характеристики траекторий, на первом листе книги, а таблицу вычисленных значений переменных на втором листе. Пусть параметры x0, y0, vx0, vy0 и dt в перечисленном порядке располагаются в ячейках B2, C2, D2, E2 и F2 Листа 1, соответственно. Тогда первые две строки таблицы значений на Листе 2, начиная со строки 4, заполняются формулами, приведенными в табл. 1. Последующие записи получаются копированием строки 5, предварительно вычислив требуемое количество строк. Размер таблицы определим из следующих
соображений. При движении по окружности радиуса,
равного 1, с характерной скоростью, равной 1,
полный оборот совершается за промежуток времени,
равный Для вычисления характеристик траектории и проверки законов Кеплера таблица значений дополнена тремя вспомогательными столбцами — F, G, H. В столбце F, начиная с первой строки таблицы, вычисляется комбинация проекций скорости и координат спутника для нахождения средней секториальной скорости на заданном промежутке времени. В столбце G с помощью функции ветвления ЕСЛИ и логического произведения И выделяются значения координаты y > 0 (столбец E4) в малой окрестности точки x = 0. Остальные ячейки столбца обнуляются. Таким образом, создается структура значений, позволяющая с помощью интервальной функции MAX найти приближенно координату точки, в которой траектория пересекает ось y, и вычислить эксцентриситет е. Аналогичная структура данных создается во вспомогательном столбце H для вычисления большой полуоси. При этом, поскольку выделяется малый диапазон отрицательных значений x, необходимо использовать функцию MIN. Соответствующие формулы приведены в табл. 2, являющейся фрагментом строки 4. Функции MIN и MAX используются в столбцах а и e таблицы результатов. Вычисления указанных характеристик производятся в таблице результатов, которая также включается в интерфейс. Период обращения определяется как значение ячейки A6280, когда получена замкнутая траектория. Среднее значение секториальной скорости, вычисленное путем усреднения формулы (9) для 20 точек в окрестности значений горизонтальной координаты, соответствующих максимальному и минимальному удалению от силового центра, помещается в раздел К2 таблицы результатов. Для реализации возможности сопоставления траекторий, соответствующих разным начальным состояниям, и проверки третьего закона Кеплера были созданы таблицы для двух траекторий, данные из которых представлялись на одной диаграмме (см. рис. 5.5). Таким образом, интерфейс представлял собой две строки параметров, две строки результатов обработки числовых данных и диаграмму с двумя графиками.
Таблица начальных значений
Рис. 5.5. Результаты эксперимента на модели MS Excel Примеры вопросов для самостоятельного решения 1. Какие в проведенных исследованиях получаются размерные первая и вторая космические скорости для спутника Земли? Ожидаемый ответ. Нужно вычислить единицу скорости для спутника у поверхности Земли: (GM/x0)1/2= (6,7 · 10-11м3/(кг · с2) · 6,0 · 1024 кг/(6,4 · 106 м))1/2 = 7,9 км/с. Для первой космической скорости это число нужно умножить на 1, а для второй — на 1,4. 2. Какие траектории спутника получатся, если начальная безразмерная скорость его меньше единицы? Ожидаемый ответ. Траекториями будут эллипсы с Землей в левом фокусе эллипса. Если начальная точка была недостаточно высоко над Землей, то траектория пересечет поверхность Земли, т.е. произойдет падение спутника на Землю. 3. Как изменятся значение площади, заметаемой радиус-вектором, и средняя секториальная скорость, если интервал времени, за который эти величины считаются, увеличить вдвое? В 5 раз? Ожидаемый ответ. Площадь увеличится в соответствующее число раз. Убедиться в этом можно, анализируя содержимое табл. 2 в разных экспериментах. Средняя секториальная скорость не изменится. Примеры заданий для самостоятельного исследования 1. Построить 11 траекторий для значений начальной скорости в диапазоне от 0,8 до 1,8. Используя режим расчета одиночной траектории, нанести на рисунок красным цветом круговую траекторию, а розовым — самую вытянутую траекторию, целиком уместившуюся на экране. 2. Произведите расчет для значений начальной скорости 0,4. Получилась ли траектория замкнутой? Как добиться, чтобы она стала замкнутой (уменьшить шаг по времени)? 3. Постройте 6 траекторий для значений начальной скорости в диапазоне от 1,4 до 1,42. Определите, сколько из них будут замкнутыми. Найдите в таблице значение большой полуоси для самой вытянутой замкнутой траектории. Попробуйте подобрать масштабы по осям x и y, чтобы эта траектория поместилась в окне графика. 4. Подобрать такую начальную скорость спутника, чтобы период его обращения T был вдвое больше, чем при обращении по круговой орбите. 5. Исследовать, как влияет величина шага по времени на значение константы третьего закона Кеплера для разных траекторий. Примечание. Количество траекторий при моделировании средствами MS Excel может быть уменьшено. 6. Закон естественного радиоактивного распадаПостроение модели явления естественного радиоактивного распада начнем с обсуждения основных свойств этого явления и постановки вопросов, на которые мы хотим получить ответы из численного эксперимента на модели. Прежде всего нужно сформулировать основные результаты натурных экспериментов. Эксперименты с тяжелыми атомами говорят, что их ядра распадаются, выбрасывая частицы и превращаясь в более легкие. Распад ядра происходит спонтанно и практически не зависит от внешних условий, в которых оно находится. Число распадов, регистрируемых в единицу времени, не зависит от внешних полей, концентрации радиоактивных атомов, химической структуры молекул, в которые входят радиоактивные атомы, а зависит только от числа атомов, ядра которых способны распадаться. Вероятность естественного распада ядра определяется его устройством и не зависит от того, что происходит вне ядра. Эта вероятность может быть описана некоторым числом, характерным для данных ядер. Таково главное свойство естественного радиоактивного распада. Вопросы для численного эксперимента на математической модели можно поставить следующим образом: 1. Как меняется со временем число нераспавшихся ядер, если в начальный момент их было N0? 2. Каково среднее время жизни T1 ядра? 3. Через какое время T2 распадется половина ядер? Ответы на первый и последний вопросы достаточно легко проверить в натурном эксперименте с быстро распадающимися ядрами. Приступим к построению математической
модели. В принятой концепции явления можно
сказать, что на малом интервале времени
Коэффициент пропорциональности
записан в таком виде, чтобы константа вещества t
имела размерность времени. Она определяет,
насколько быстро распадаются ядра данного
вещества. В теории радиоактивного распада обычно
используют другую постоянную Для полного определения функции N(t) нужно задать число ядер вещества в начальный момент: t = 0: N = N0. (6.2) Уравнения (6.1)–(6.2) определяют математическую модель радиоактивного распада. Теперь в модели нужно перейти к относительным единицам, чтобы уменьшить число параметров задачи и представить результаты численного эксперимента в относительных единицах. В качестве характерного времени
процесса можно взять В качестве характерного числа атомов
возьмем их количество в момент t = 0, т.е.
представим число атомов в произвольный момент
времени в виде
Уравнения (6.3) позволяют решить задачу о законе радиоактивного распада и ответить на поставленные к модели вопросы. Все входящие в (6.3) величины безразмерные, поэтому в дальнейшем знак безразмерной величины “~” писать не будем. Перейдем к описанию алгоритма
вычисления числа ядер, не распавшихся к моменту
времени t. Вдоль оси времени будем
продвигаться малыми, но конечными шагами
величиной
Запись в правой части уравнения (6.4)
числа ядер на левом конце временного интервала N0 = 1, Nn+1 = Nn
– Nn· Система уравнений (6.5) определяет число нераспавшихся ядер в последовательные моменты времени. Обратим внимание на то, что она не содержит характеристик вещества: полученные при численном эксперименте свойства распада будут универсальными. Индивидуальность ядер проявится только через масштаб времени t. Вернемся к вопросам, поставленным перед численным экспериментом. Для определения зависимости N(t) по вычисленным значениям Nn нужно построить плавную кривую процесса. Чтобы вычислить среднее время жизни ядра T1, нужно просуммировать время жизни каждого из ядер и разделить его на полное число распавшихся ядер. Время жизни tn имеют те ядра, которые распались на интервале tn+1 – tn. Их число есть Nn – Nn+1. Отсюда получим
Для вычисления времени Т2, за которое распадается половина начального числа ядер, нужно найти для определяемой в численном эксперименте функции N(t) решение уравнения N(t) = 0,5. Таким образом, правила получения ответов на все поставленные вопросы сформулированы. Эксперимент на модели в среде Delphi Среда моделирования данной задачи подобна использованным выше и будет содержать три окна: · главное с основными органами управления процессом численного моделирования, · окна построения графиков, · окна с таблицей физических характеристик процесса. Для проведения эксперимента
необходимо определиться со значениями
параметров расчетной модели — полного времени
расчета распада Тmax и шага по времени dt ( Имеющиеся в верхнем окне органы управления позволяют провести полное исследование физической модели естественного радиоактивного распада. Можно пробовать рисовать различные графики распада и стирать их, подбирая именно те значения параметра, которые требуется найти в соответствии с целью исследования, в частности, в соответствии с поставленным учителем заданием. Итак, для начала эксперимента зададим dt = 0,1
(оно должно быть много меньше единицы),
Рис. 6.1. Результаты эксперимента по радиоактивному распаду Примеры заданий для самостоятельного исследования 1. Построить график распада до времени T2 и T1 и оценить долю распавшихся ядер. Для этого на фоне черного графика полного распада вначале построить красный график распада до T1, а затем синий график распада до Т2. 2. Используя технику наложения графиков в задании 1, построить разными цветами графики распада до Т2/2, Т2, 1,5 · Т2, 2 · Т2, 2,5 · Т2 и 3 · Т2. Эксперимент на модели в среде MS Excel
Рис. 6.2. Результаты эксперимента В качестве самостоятельного задания можно предложить убедиться в том, что за промежуток времени, равный периоду полураспада, количество ядер действительно уменьшается в два раза, подбирая соответствующим образом шаг по времени. 7. Броуновское движениеПостановка задачи Броуновским движением называют наблюдающееся под микроскопом непрерывное хаотическое движение мелких частиц, взвешенных в жидкости или газе. Молекулы среды находятся в непрерывном тепловом движении и при столкновении с частицей передают ей соответствующий импульс. Если размеры частицы достаточно малы (меньше 10-4 см), то удары, получаемые частицей с разных сторон, не компенсируют друг друга в силу их небольшого количества. Под влиянием этих флуктуаций давления на поверхности частицы она приходит в беспорядочное движение, направление и скорость которого меняются с большой частотой (около 1012 раз в секунду). В микроскоп видно мелкое дрожание и смещение частицы. Чтобы анализировать это движение, экспериментатор фиксирует положение частицы через равные промежутки времени, например, через 30 сек., и соединяет их прямыми линиями. Какие основные особенности броуновского движения можно установить из этих наблюдений? · В каждый момент времени частица может с одинаковой вероятностью переместиться по любому направлению. · Величина этого смещения также случайна и зависит от свойств жидкости, ее температуры и размеров частицы. · Для фиксированной системы имеется некоторое среднее за один такт наблюдения смещение l, которое возрастает с ростом температуры и уменьшением вязкости жидкости. Эти знания о броуновском движении мы положим в основу численной модели. Экспериментируя с моделью, мы хотим получить типичные “траектории” броуновской частицы и определить среднее расстояние, на которое проходит броуновская частица за большой интервал времени наблюдения t. Численная модель Положение броуновской частицы будем задавать в декартовой системе координат. В начальный момент пусть частица находится в начале координат. Смещение частицы вдоль каждой из осей является случайным со средним по величине смещением l и равновероятным в обоих направлениях. Это смещение будем формировать с помощью стандартного датчика случайных чисел random с равномерным распределением от 0 до 1:
Координаты нового положения частицы в последовательные моменты времени будем определять так:
Соответствующий момент времени будет Эксперимент на модели в среде Delphi Для получения типичных траекторий броуновской частицы проведем расчет четырех траекторий для l = 1 по одной, меняя их цвет. На рис. 7.1 показаны результаты этого численного эксперимента. Обратите внимание на то, какие сложные и неповторяющиеся траектории получаются.
Рис.7.1. Траектории четырех броуновских частиц Обратимся к табл. 2 компьютерной модели, показывающей расстояния, на которые уходила частица от начала координат к моменту времени, указанному в верхней строке. Видно, что это расстояние для одной траектории меняется нерегулярно. Сравните эти расстояния для нескольких траекторий, оценивая среднее расстояние. Эта величина ведет себя более регулярно. В табл. 1 в пяти последовательных строках показаны средние квадраты смещения частицы (s2) за одинаковые промежутки времени (интервал указан в столбце Т, определяется значением правого нижнего окна в табл. 2) вдоль одной траектории и затем еще раз усредненные по серии траекторий. Зависимость среднего квадрата s2 от величины временного интервала для каждой траектории можно получить нажатием клавиши “Построить” на итоговом графике. На рис. 7.2 представлены результаты этого построения.
Рис.7.2. Зависимость среднегоквадрата смещения броуновской частицы от времени наблюдения Красные кружки отмечают четыре почти совпадающие линейные зависимости. Этот результат говорит о том, что средний квадрат смещения частицы за время Т пропорционален этому времени. Теперь можно провести наблюдение за движением большой серии частиц (по 10 траекторий), меняя и временной интервал выдачи положения частицы (правое нижнее окно табл. 2). Добавленные точки на итоговом графике подтверждают установленную ранее закономерность. Примеры вопросов для самостоятельного решения 1. Как часто броуновская частица возвращается назад к началу координат, т.е. расстояние до начала координат в фиксируемый момент времени оказывается меньше, чем в предыдущий? Ожидаемый ответ: Подсчет возвратов частицы в табл. 2 показывает, что они составляют около одной третьей части и случаются нерегулярно. Примеры заданий для самостоятельного исследования 1. Проведите серию экспериментов с разными L (по смыслу это соответствует разным температурам жидкости, в которой взвешена броуновская частица). Табл. 1 чистить не будем, чтобы сохранить полученные точки на итоговом графике, а поле для построения траекторий удобно чистить после каждой серии. Проведите сразу несколько серий расчетов по 10 траекторий и постройте итоговый график. Экспериментальные точки должны группироваться около прямых с разным наклоном. 2. В главном окне показан меняющийся параметр N, который определяет количество обращений к датчику случайных чисел. При N = 1 для расчета одного шага броуновской частицы используется равномерное распределение, для больших N это распределение переходит в распределение Гаусса (чем больше, тем лучше). Определите, влияет ли значение параметра N на зависимость среднего квадрата смещения броуновской частицы от времени наблюдения. 3. Проследите зависимость среднего квадрата смещения от L. Для этого выпишите значения s2 для разных L и одинаковых значений Т и постройте зависимость s2 от L. Эксперимент на модели в среде MS Excel Общая структура данного проекта соответствует той, что описана во введении. В качестве результатов представлены положения броуновской частицы в последовательные моменты времени, при условии, что в начальный момент времени частица находилась в начале координат. Для определения ее положения в последующие моменты времени использовался встроенный датчик случайных чисел с диапазоном (–1, 1). На второй диаграмме представлена зависимость от времени квадрата расстояний от начальной точки до текущего положения частицы. Видно, что в среднем это расстояние растет со временем. В качестве самостоятельного задания можно предложить рассмотреть разные реализации, пересчитывая значения, помещенные в таблицу.
|

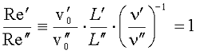 (1.2)
(1.2)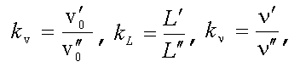
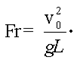 .
.
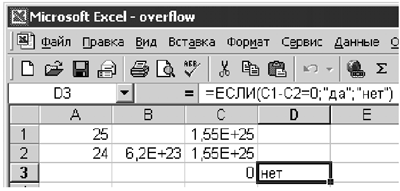
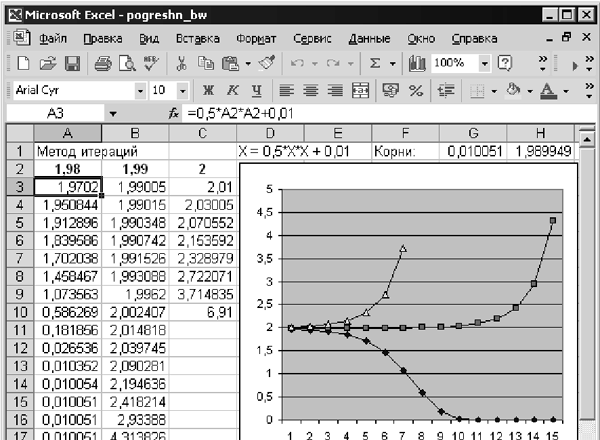
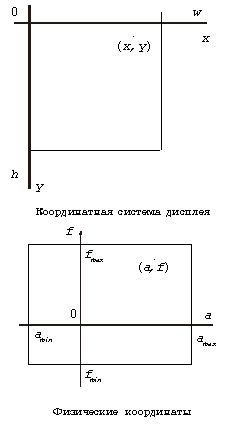
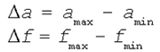
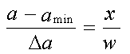
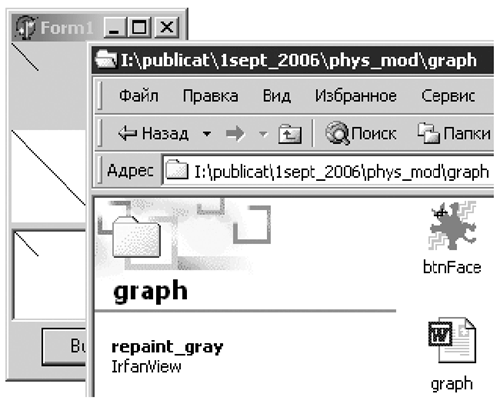
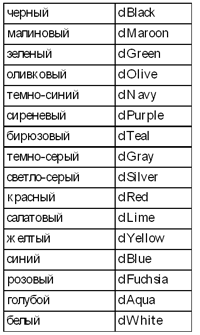
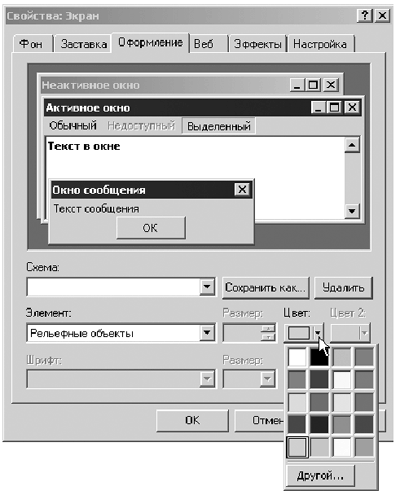
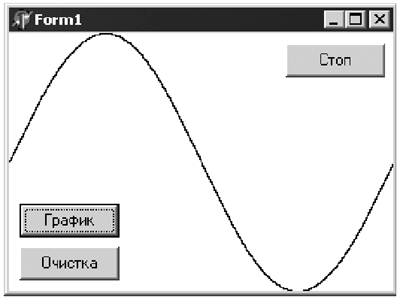

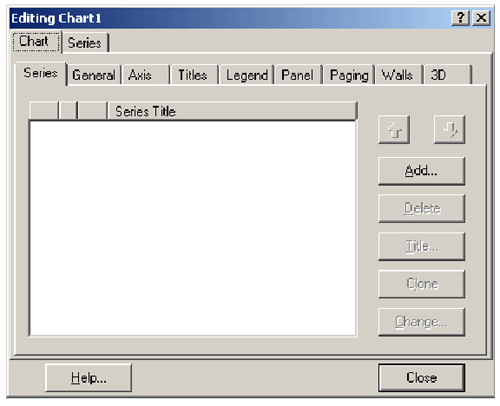
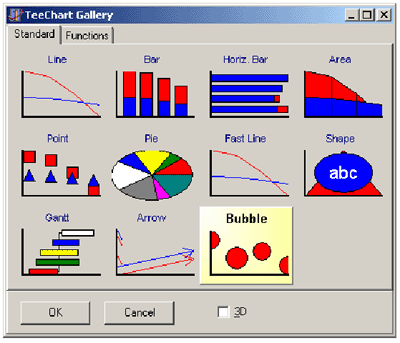
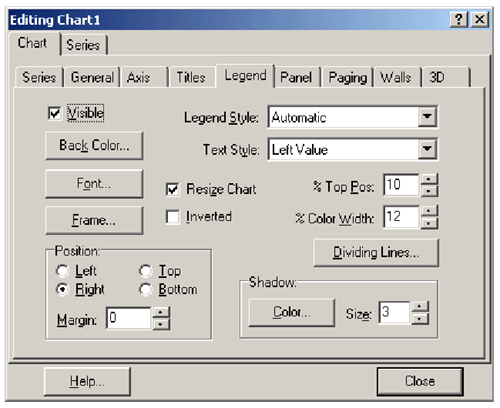
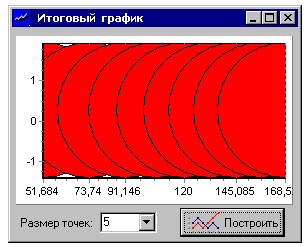
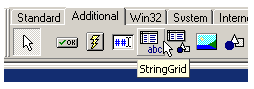
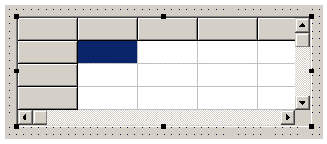
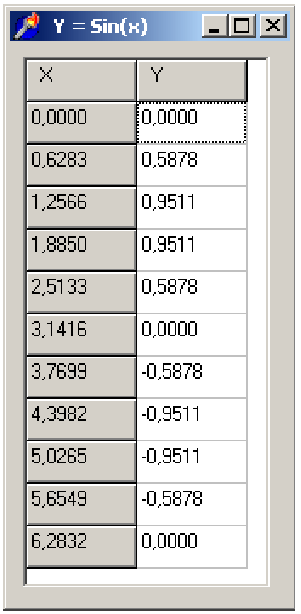
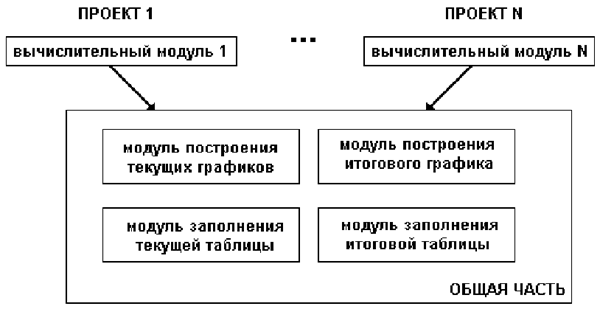
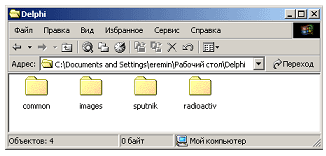
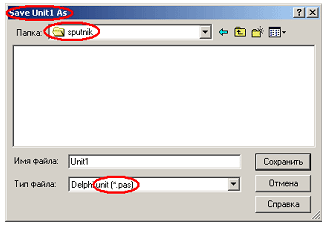
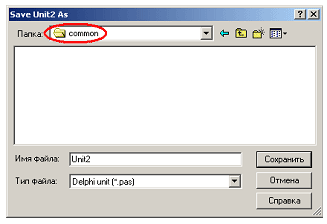
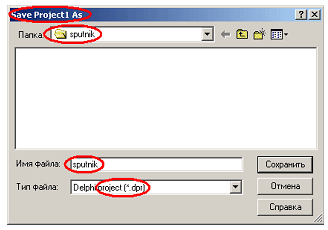
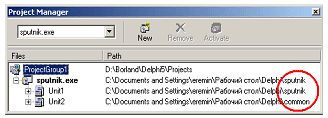
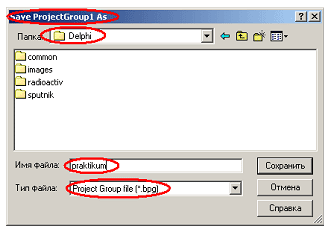
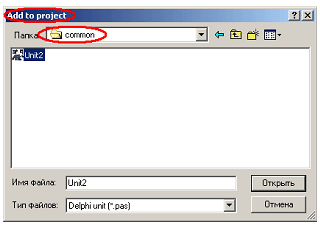
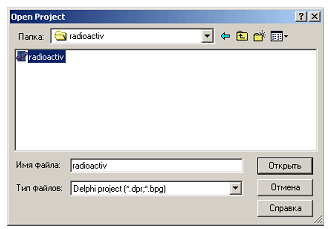
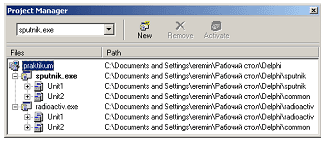
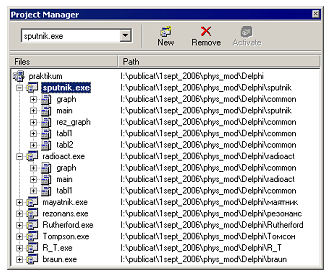
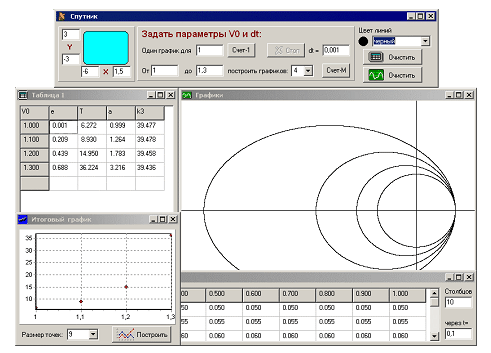
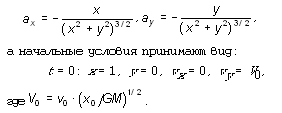 (5.3), (5.4)
(5.3), (5.4)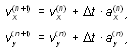 (5.5), (5.6)
(5.5), (5.6)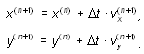 (5.7). (5.8)
(5.7). (5.8)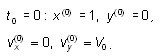 .
.