ЖАРКОЕ ЛЕТО-2006
Компьютерные модели в школьном курсе физики
Р.В. Бирих, Е.А. Еремин, В.А.
Чернатынский
Окончание. Начало см. в № 14/2006
8. Модели атома
После открытия Дж. Дж. Томсона в
1903 году электрона стало ясно, что нейтральный
атом, кроме положительно заряженных частиц,
должен содержать электроны. Модель атома,
которую предложил Дж. Дж. Томсон,
представляла собой положительно заряженную
сферу, внутри которой, как изюминки в булочке,
расположены электроны.
Ответить на вопрос о том, как
действительно устроен атом, могли бы
эксперименты по рассеиванию на атоме заряженных
частиц. Такие натурные эксперименты были
проведены под руководством Э.Резерфорда. Обсудим
идеи этих экспериментов. В качестве источника
заряженных частиц использовался кусочек
радиоактивного препарата (радий), испытывающий  -распад.
Особенностью -распад.
Особенностью  -распада
является то, что вылетающие частицы имеют
практически одинаковую скорость. С помощью
свинцовых диафрагм выделялся тонкий пучок -распада
является то, что вылетающие частицы имеют
практически одинаковую скорость. С помощью
свинцовых диафрагм выделялся тонкий пучок  -частиц, который
направлялся на очень тонкую золотую фольгу. При
прохождении через фольгу -частиц, который
направлялся на очень тонкую золотую фольгу. При
прохождении через фольгу  -частицы рассеивались под разными углами
к направлению первоначального полета.
Распределение по углам измерялось по вспышкам на
флюоресцирующем экране с помощью микроскопа. На рис. 8.1
представлена схема экспериментальной установки.
Закон распределения рассеянных частиц
определяется характером взаимодействия
заряженной частицы с атомом рассеивающего
вещества, и из результатов эксперимента
Резерфорд надеялся понять, как устроен атом. Если
нейтральный атом представляет собой сплошной
шар (условно назовем модель Томсона), то -частицы рассеивались под разными углами
к направлению первоначального полета.
Распределение по углам измерялось по вспышкам на
флюоресцирующем экране с помощью микроскопа. На рис. 8.1
представлена схема экспериментальной установки.
Закон распределения рассеянных частиц
определяется характером взаимодействия
заряженной частицы с атомом рассеивающего
вещества, и из результатов эксперимента
Резерфорд надеялся понять, как устроен атом. Если
нейтральный атом представляет собой сплошной
шар (условно назовем модель Томсона), то  -частица будет
отскакивать от атома по законам упругого
столкновения шаров. Если в нейтральном атоме
имеется неоднородность в распределении зарядов
и частица проникает в атом, то структура атома
будет отражена в законе рассеивания заряженной
частицы. -частица будет
отскакивать от атома по законам упругого
столкновения шаров. Если в нейтральном атоме
имеется неоднородность в распределении зарядов
и частица проникает в атом, то структура атома
будет отражена в законе рассеивания заряженной
частицы.
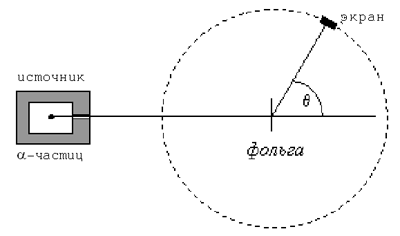
Рис. 8.1. Схема установки по рассеиванию
частиц
Как происходит рассеивание частиц и
как меняется их траектория в окрестности
рассеивающего центра, показано на рис. 8.2.
Рассеивающий центр (атом золота) находится в
начале координат. Слева очень далеко (на
бесконечности) находится однородный источник
частиц, скорость которых vo одинакова и
направлена вдоль оси х. Частица, находившаяся
на расстоянии p от оси х, вначале
двигается вдоль прямой, параллельной оси х, а
затем, в результате взаимодействия с атомом,
отклоняется от этой прямой. Улетев на достаточно
большое расстояние от атома, она снова двигается
равномерно и прямолинейно, но теперь под углом 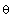 к оси х. В силу
осевой симметрии задачи все частицы, вылетевшие
из кольца с радиусом p и толщиной dp,
рассеиваются на угол к оси х. В силу
осевой симметрии задачи все частицы, вылетевшие
из кольца с радиусом p и толщиной dp,
рассеиваются на угол 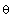 в кольцо толщиной d в кольцо толщиной d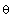 на сфере с центром в начале
координат. Если источник частиц обеспечивает
однородный поток частиц с плотностью n с
постоянной скоростью, то число частиц,
попадающих на экран, который из рассеивающего
центра виден под телесным углом dW, можно
вычислить по формуле на сфере с центром в начале
координат. Если источник частиц обеспечивает
однородный поток частиц с плотностью n с
постоянной скоростью, то число частиц,
попадающих на экран, который из рассеивающего
центра виден под телесным углом dW, можно
вычислить по формуле
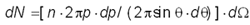 . .
Величину 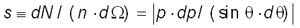 , называемую дифференциальным сечением
рассеивания, можно измерить как функцию , называемую дифференциальным сечением
рассеивания, можно измерить как функцию 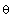 в натурном
эксперименте и в численном эксперименте с
заданным законом взаимодействия в натурном
эксперименте и в численном эксперименте с
заданным законом взаимодействия  -частицы и атома. Сравнение
этих результатов позволяет выбрать правильный
закон взаимодействия и, следовательно,
определить устройство атома. -частицы и атома. Сравнение
этих результатов позволяет выбрать правильный
закон взаимодействия и, следовательно,
определить устройство атома.
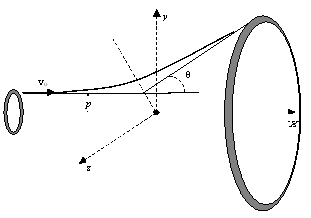
Рис. 8.2. Система координат и схема
расеивания
Упругое рассеивание частиц (модель Томсона)
Постановка задачи и численная модель
В модели Дж. Дж. Томсона атом
представляет собой тяжелую электрически
нейтральную частицу. Если она непроницаема для  -частицы, то в
эксперименте должно наблюдаться упругое
рассеивание -частицы, то в
эксперименте должно наблюдаться упругое
рассеивание  -частиц.
До атома -частиц.
До атома  -частица
летит по прямой с постоянной скоростью, на
поверхности атома происходит упругое
рассеивание: касательная компонента скорости
a-частицы остается неизменной, а нормальная
компонента скорости меняет знак (предполагается,
что атом имеет массу, много большую массы
частицы). Далее происходит свободный полет
частицы по прямой. -частица
летит по прямой с постоянной скоростью, на
поверхности атома происходит упругое
рассеивание: касательная компонента скорости
a-частицы остается неизменной, а нормальная
компонента скорости меняет знак (предполагается,
что атом имеет массу, много большую массы
частицы). Далее происходит свободный полет
частицы по прямой.
Запишем уравнения движения  -частицы. Пусть на большом
расстоянии от атома, который мы представляем как
сферу радиуса а, летит -частицы. Пусть на большом
расстоянии от атома, который мы представляем как
сферу радиуса а, летит  -частица со скоростью v0 вдоль оси х
на прицельном расстоянии p. Частица все время
будет двигаться в одной плоскости, которую мы на рис.
8.2 обозначили xy; угол рассеивания q будет
зависеть от прицельного расстояния р. Для
записи уравнений в безразмерных единицах
выберем в качестве единицы расстояния радиус
атома а, единицы скорости — v0 скорость -частица со скоростью v0 вдоль оси х
на прицельном расстоянии p. Частица все время
будет двигаться в одной плоскости, которую мы на рис.
8.2 обозначили xy; угол рассеивания q будет
зависеть от прицельного расстояния р. Для
записи уравнений в безразмерных единицах
выберем в качестве единицы расстояния радиус
атома а, единицы скорости — v0 скорость  -частицы в начальный
момент времени, единицы времени — а/v0. В
проекциях на оси координат задачу о вычислении
скорости частицы и ее положения в
последовательные моменты времени tn можно
сформулировать так: -частицы в начальный
момент времени, единицы времени — а/v0. В
проекциях на оси координат задачу о вычислении
скорости частицы и ее положения в
последовательные моменты времени tn можно
сформулировать так:
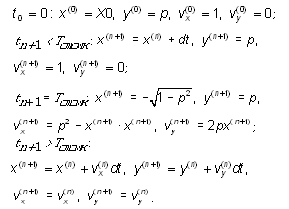 ; ;
Момент столкновения частицы с атомом
при малом dt можно определить по условию 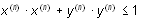 . После построения
всей траектории можно вычислить угол
рассеивания q и значение параметра s. Для его
вычисления строится траектория с близким к
заданному p прицельным расстоянием (в
приведенном ниже алгоритме Dр принималось
равным 0,0001). . После построения
всей траектории можно вычислить угол
рассеивания q и значение параметра s. Для его
вычисления строится траектория с близким к
заданному p прицельным расстоянием (в
приведенном ниже алгоритме Dр принималось
равным 0,0001).
Моделирование задачи в среде Delphi
В предлагаемой виртуальной среде
модели Томсона и Резерфорда объединены в одну
программу. Вид основного окна с органами
управления показан на рис. 8.3. Все кнопки и
окна имеют такие же функции, как в предыдущей
задаче. Добавлено лишь окно моделей.

Рис. 8.3. Вид окна управления решением
задач
по рассеиванию частиц
Эксперимент на модели в среде Delphi
Проведем экспериментальное
исследование закона упругого рассеивания. В окне
моделей выберем модель Томсона. Для проведения
численного эксперимента нужно прежде всего
выбрать шаг по времени dt, с которым будем
строить траекторию. Хотя при равномерном
движении на прямолинейных участках траектории
величина шага по времени не играет существенной
роли, в предложенном алгоритме построения
траекторий полета  -частицы он должен быть взят достаточно
малым, чтобы аккуратно зафиксировать момент
столкновения a-частицы с атомом. Шаг не должен
быть и слишком маленьким, так как в этом случае
для построения траектории потребуется заметное
время. Поскольку в качестве масштабов мы выбрали
характерные параметры системы, то типичный
временной интервал жизни системы равен
1. Малый интервал dt поэтому должен быть много
меньше единицы; выберем его, например, равным 0,001.
Второй параметр, который нужно задать, это
прицельное расстояние. Опять, пользуясь тем, что
расчет ведется в собственных масштабах задачи,
прицельное расстояние, очевидно, должно быть
меньше единицы. Для первого эксперимента можно
положить р = 0,5. Построим одну
траекторию, нажав кнопку “Счет-1”. Траектория
удовлетворяет ожидаемым требованиям. В табл. 1
приведены интегральные характеристики
траектории: в первом столбце приведено значение
прицельного расстояния для рассчитанной
траектории, во втором — угол рассеивания -частицы он должен быть взят достаточно
малым, чтобы аккуратно зафиксировать момент
столкновения a-частицы с атомом. Шаг не должен
быть и слишком маленьким, так как в этом случае
для построения траектории потребуется заметное
время. Поскольку в качестве масштабов мы выбрали
характерные параметры системы, то типичный
временной интервал жизни системы равен
1. Малый интервал dt поэтому должен быть много
меньше единицы; выберем его, например, равным 0,001.
Второй параметр, который нужно задать, это
прицельное расстояние. Опять, пользуясь тем, что
расчет ведется в собственных масштабах задачи,
прицельное расстояние, очевидно, должно быть
меньше единицы. Для первого эксперимента можно
положить р = 0,5. Построим одну
траекторию, нажав кнопку “Счет-1”. Траектория
удовлетворяет ожидаемым требованиям. В табл. 1
приведены интегральные характеристики
траектории: в первом столбце приведено значение
прицельного расстояния для рассчитанной
траектории, во втором — угол рассеивания 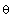 , в третьем —
минимальное расстояние, на которое подлетает
частица к атому, в четвертом — дифференциальное
сечение рассеивания s, в пятом столбце
приведена величина, которая характеризует, как
быстро меняется угол рассеивания с изменением
прицельного расстояния. В табл. 2 в безразмерных
единицах приведено значение кинетической
энергии , в третьем —
минимальное расстояние, на которое подлетает
частица к атому, в четвертом — дифференциальное
сечение рассеивания s, в пятом столбце
приведена величина, которая характеризует, как
быстро меняется угол рассеивания с изменением
прицельного расстояния. В табл. 2 в безразмерных
единицах приведено значение кинетической
энергии  -частицы
в разные моменты времени полета частицы. Моменты
времени указаны в верхней строке таблицы. -частицы
в разные моменты времени полета частицы. Моменты
времени указаны в верхней строке таблицы.
Посмотрим теперь, как меняется угол
рассеивания при изменении прицельного
расстояния. Для этого построим серию из 11
траекторий с прицельными расстояниями от –0,99 до
0,99. Траектории с p = ±1 соответствуют случаю,
когда  -частица
касается рассеивающего атома в крайних точках и
не меняет траектории. Дифференциальное сечение
рассеивания и скорость изменения угла
рассеивания для этих траекторий не определены,
поэтому мы их исключили из расчета. На рис. 8.4
показан вид экрана после проведения
эксперимента. -частица
касается рассеивающего атома в крайних точках и
не меняет траектории. Дифференциальное сечение
рассеивания и скорость изменения угла
рассеивания для этих траекторий не определены,
поэтому мы их исключили из расчета. На рис. 8.4
показан вид экрана после проведения
эксперимента.
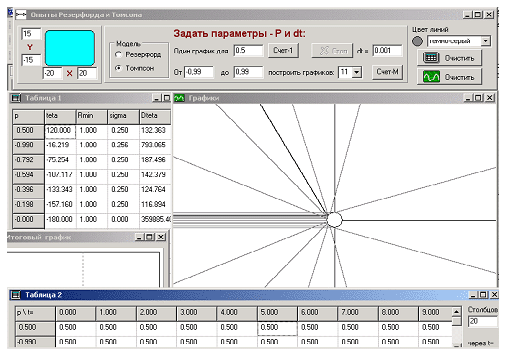
Рис.8.4. Результаты по рассеиванию в
модели Томсона
При прицельном расстоянии меньшем
единицы частицы рассеиваются равномерно по всем
углам. Об этом говорит тот факт, что
дифференциальное сечение рассеивания одинаково
для всех прицельных расстояний, по модулю
меньших единицы. Из табл. 2 видно, что, как и
следовало ожидать, кинетическая энергия частиц
не изменяется: они совершают полет без силового
воздействия и испытывают на атоме упругое
столкновение.
Примеры вопросов для самостоятельного решения
1. Как изменится число частиц, летящих в
заданный телесный угол, если имеется N рассеивающих
центров, расположенных в одной плоскости,
перпендикулярной потоку частиц?
Ожидаемый ответ. Число частиц
увеличится в N раз, так как от каждого
рассеивающего центра под заданным углом
рассеивается одинаковое количество частиц.
Примеры заданий для самостоятельного
исследования
1. Определить траекторию, которая дает
отклонение частицы на 90°.
2. Разным цветом нарисовать траектории
с прицельными расстояниями, близкими к 1.
Обратите внимание, как быстро меняется угол
рассеивания с изменением р.
Эксперимент на модели в среде MS Excel
Отличительной чертой данного проекта
является использование в таблице условного
выражения для того, чтобы учесть изменение
направления движения  -частицы при столкновении с поверхностью
сферы. -частицы при столкновении с поверхностью
сферы.
На модели в MS Excel удобно полет частицы
организовать справа налево.
В качестве самостоятельных заданий
можно порекомендовать те же, что сформулированы
к проекту DELPHI.
Рассеивание  -частиц
на кулоновском центре -частиц
на кулоновском центре
Постановка задачи
Рассмотрим рассеивание быстро летящих
заряженных частиц кулоновским электрическим
полем, создаваемым ядром тяжелого атома. Наш
численный эксперимент должен будет моделировать
известные опыты Резерфорда по измерению углов
рассеивания  -частиц
ядрами очень тонкой золотой фольги. В модели
будем считать, что имеется одно неподвижное ядро
с зарядом eZ, которое находится в начале
координат. На большом расстоянии от ядра вдоль
оси x на прицельном расстоянии p летит
a-частица со скоростью v0. Поскольку сила,
действующая на частицу, центральная, она будет
двигаться в плоскости x, y, задаваемой
векторами r0 и v0. Угол рассеивания частиц -частиц
ядрами очень тонкой золотой фольги. В модели
будем считать, что имеется одно неподвижное ядро
с зарядом eZ, которое находится в начале
координат. На большом расстоянии от ядра вдоль
оси x на прицельном расстоянии p летит
a-частица со скоростью v0. Поскольку сила,
действующая на частицу, центральная, она будет
двигаться в плоскости x, y, задаваемой
векторами r0 и v0. Угол рассеивания частиц 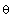 будет зависеть от
прицельного расстояния (см. рис. 8.1). будет зависеть от
прицельного расстояния (см. рис. 8.1).
Запишем уравнения движения частицы в
проекциях на оси введенной системы координат
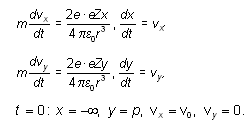
Для формулировки задачи в
безразмерных переменных выберем единицы
измерения длины, времени и скорости.
Характерного масштаба длины на первый взгляд не
видно, поэтому мы его обозначим l и
окончательно определим из требования простоты
для коэффициентов уравнений. В задаче имеется
характерная скорость v0, с которой  -частицы выбрасываются из
источника. Эта скорость во всех экспериментах
постоянна, поэтому ее удобно взять в качестве
масштаба скоростей. Единицу времени определим
как отношение единицы длины к единице скорости.
Таким образом, имеем -частицы выбрасываются из
источника. Эта скорость во всех экспериментах
постоянна, поэтому ее удобно взять в качестве
масштаба скоростей. Единицу времени определим
как отношение единицы длины к единице скорости.
Таким образом, имеем
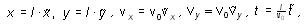
где знаком “~” отмечены безразмерные
величины.
В безразмерных переменных уравнения
движения принимают вид
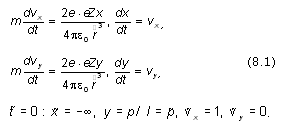
Теперь удобно распорядиться величиной
l так, чтобы коэффициент в уравнении Ньютона
стал равен 1, т.е. положить
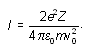 . (8.2)
. (8.2)
В таких безразмерных единицах
ускорение, испытываемое  -частицей, и начальные условия принимают
вид (поскольку все входящие в уравнения величины
безразмерные, знак безразмерной величины “~”
опущен) -частицей, и начальные условия принимают
вид (поскольку все входящие в уравнения величины
безразмерные, знак безразмерной величины “~”
опущен)
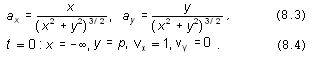
Численная модель
Для вычисления в различные моменты
времени проекций скорости a-частицы и ее
координат на временной оси выберем дискретные
точки tn, отстоящие друг от друга на малые
интервалы Dt. Тогда проекции скорости vx(n+1)
и vy(n+1) в момент времени tn+1 будут
приближенно (считаем, что ускорение на этом
интервале времени не изменилось) представляться
выражениями
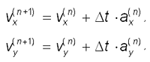 (8.5), (8.6)
(8.5), (8.6)
а координаты в этот момент будем
вычислять, как при равномерном движении (опять
считая, что интервал времени Dt мал, и скорость
в течение него такая, как в конце интервала):
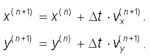 (8.7), (8.8)
(8.7), (8.8)
В начальный момент времени проекции
скорости и координаты a-частицы известны:
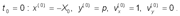 . .
Система (8.5)–(8.8) позволяет шаг за шагом,
при малом Dt, достаточно точно вычислить
траекторию  -частицы
и угол, на который она рассеялась. Значение
константы Х0, задающей начальное
положение -частицы
и угол, на который она рассеялась. Значение
константы Х0, задающей начальное
положение  -частицы,
должно быть достаточно большим. В численном
эксперименте ее значение принималось равным 20.
Таким же принималось расстояние, на котором
вычислялся угол рассеивания. -частицы,
должно быть достаточно большим. В численном
эксперименте ее значение принималось равным 20.
Таким же принималось расстояние, на котором
вычислялся угол рассеивания.
Эксперимент на модели в среде Delphi
Проведем экспериментальное
исследование рассеивания a-частиц на кулоновском
центре рассеивания. В окне модели основного окна
проекта Резерфорд — Томсон выберем модель
Резерфорда. Выберем интервал времени, через
который будем вычислять новое положение частицы
и ее скорость. Поскольку он должен быть
достаточно малым, выберем dt = 0,01.
Напомним, что расчет ведется в безразмерных
единицах, так что эта величина действительно
малая, по сравнению с 1. Прицельное расстояние для
первой траектории выберем равным 1 и построим эту
траекторию. Заметим, что окружность в начале
координат, проведенная радиусом 1, представляет
положительно заряженное ядро атома. Чтобы
определить, насколько точно рассчитана
траектория, уменьшим шаг интегрирования, взяв dt = 0,001.
Сменим цвет кривой и проведем расчет новой
траектории. Графики двух построенных кривых
практически совпадают, но угол рассеивания в
третьей значащей цифре отличается. Проведем еще
один эксперимент с dt = 0,0001. Теперь
различие в угле рассеивания составляет одну
единицу в четвертом знаке. Такой результат по
точности можно считать удовлетворительным, и
построение кривой занимает приемлемое время.

Рис.8.6. Траектории a-частиц, рассеянных
на кулоновском центре
Приступим теперь к систематическому
исследованию закона рассеивания. Для получения
общего представления о характере рассеивания
построим серию из 11 траекторий с прицельными
расстояниями от –2 до 2. Очистим таблицы и экран.
Кнопкой “Счет-М” запускаем программу на счет
серии траекторий. Мы видим симметричное
рассеивание на положительные и отрицательные
углы. Распределение рассеянных частиц по углам
неравномерное. Для получения более подробной
зависимости дифференциального сечения
рассеивания от угла построим 11 траекторий с
прицельными расстояниями от 2 до 4 и от –4 до –2, а
затем еще несколько траекторий в режиме
построения одиночных траекторий. На рис. 8.6
приведены траектории этой серии частиц.
Эксперимент показывает, что
большинство частиц рассеиваются на малые углы.
На большие углы рассеиваются частицы, летящие на
прицельных расстояниях, меньших единицы.
Наименьшее расстояние, на которое подлетают
частицы, около двух единиц. В табл. 2 показано, как
изменяется в процессе движения кинетическая
энергия частиц (она измерена в относительных
единицах). По мере приближения к ядру частица
тормозится, и ее кинетическая энергия
уменьшается. После рассеивания частиц
электрическим полем разгонятся до прежней по
величине скорости.
В окне итоговый график построим
зависимость дифференциального сечения
рассеивания от угла 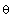 . Этот график показывает заметное
увеличение числа частиц, рассеивающихся под
малыми углами. Закон изменения
дифференциального сечения в нашем эксперименте
совпадает с результатами натурного эксперимента
Э.Резерфорда. . Этот график показывает заметное
увеличение числа частиц, рассеивающихся под
малыми углами. Закон изменения
дифференциального сечения в нашем эксперименте
совпадает с результатами натурного эксперимента
Э.Резерфорда.  -частица
рассеивается кулоновским полем ядра. Размер ядра
в принятых единицах измерения имеет размер
порядка 1. -частица
рассеивается кулоновским полем ядра. Размер ядра
в принятых единицах измерения имеет размер
порядка 1.
Для сравнения моделей рассеивания на
уже полученных графиках достроим кривые в модели
Томсона. Для этого, не производя очистки поля
графиков и таблиц, перейдем к модели Томсона и
построим серию траекторий с прицельными
расстояниями от –0,99 до 0,99. В поле “Итоговый
график” проведем построение кривых. На рис. 8.7
приведена зависимость дифференциального
сечения рассеивания от угла рассеивания для
обеих моделей. Для модели Томсона это
горизонтальная линия в нижней части графика.
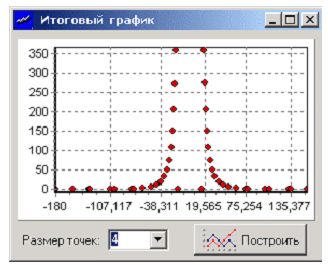
Рис. 8.7. Зависимость
дифференциального сечения от угла рассеивания
для обеих моделей
Примеры вопросов для самостоятельного решения
1. Каков порядок размера ядра в метрах,
если в принятых единицах его размер равен 1?
Ожидаемый ответ. Если  -частица, испущенная при распаде
радия, рассеивается на атоме золота, то -частица, испущенная при распаде
радия, рассеивается на атоме золота, то 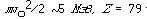 и и
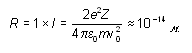
Примеры заданий для самостоятельного
исследования
1. В численном эксперименте найти
прицельное расстояние, при котором  -частица рассеивается под
углом 90°. -частица рассеивается под
углом 90°.
2. Найти прицельные расстояния, при
которых  -частица
рассеивается под углами, меньшими 15°. Каково при
этом дифференциальное сечение рассеивания? -частица
рассеивается под углами, меньшими 15°. Каково при
этом дифференциальное сечение рассеивания?
Эксперимент на модели в среде MS Excel
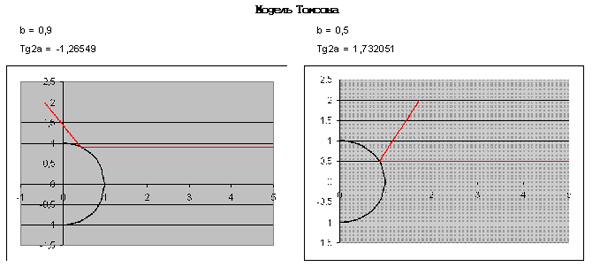
Структура проекта соответствует той,
что описана во введении. На диаграммах
изображены траектории  -частицы для двух значений прицельного
расстояния. Как видно, в зависимости от значения
прицельного расстояния может быть рассеяние
вперед и рассеяние назад. -частицы для двух значений прицельного
расстояния. Как видно, в зависимости от значения
прицельного расстояния может быть рассеяние
вперед и рассеяние назад.
В качестве самостоятельного
исследования можно предложить те же задания, что
сформулированы по модели DELPHI.
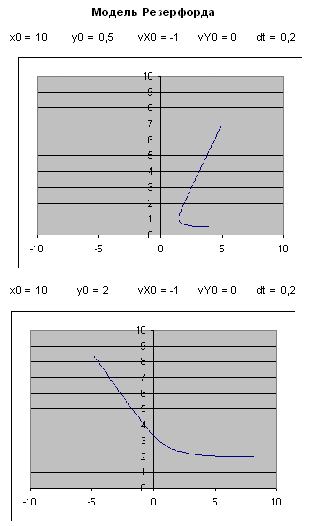
Рис. 8.8. Результаты эксперимента
на модели MS Excel
9. Колебательные системы
Перейдем к исследованию колебательных
систем. Типичными представителями этих систем
являются математический маятник, пружинный
маятник, электрические цепи, содержащие
колебательный контур. Особенность поведения
колебательной системы состоит в том, что ее
состояние через определенный один и тот же
интервал времени повторяется точно или
приближенно. В первом случае процесс называют
периодическим, а во втором — квазипериодическим.
Так как для исследования возможных состояний
колебательной системы часто приходится
наблюдать несколько периодов колебаний, для
описания чередований ее состояний используют
фазовое пространство. У математического и
пружинного маятников фазовое пространство имеет
два измерения (фазовая плоскость), и в качестве
его координат выбирают величину отклонения
маятника от положения равновесия и скорость
движения маятника.
В случае электрического контура в качестве
координат фазового пространства удобно взять
величину заряда на конденсаторе и силу тока в
катушке индуктивности. Линия, на которую ложатся
последовательные состояния системы, называется
фазовой траекторией. Если эта линия замкнутая, то
мы имеем дело с периодическим процессом.
Далее мы рассмотрим два примера
колебательных систем: 1) математический маятник,
совершающий конечные колебания и имеющий
нелинейную возвращающую силу, и 2) электрический
колебательный контур с сопротивлением и
периодической внешней эдс.
Математический маятник
Постановка задачи
Пусть к свободному концу невесомого
стержня длиной l , имеющего возможность без
трения поворачиваться в вертикальной плоскости
вокруг оси O, прикреплена материальная точка
с массой m (грузик) (рис. 9.1). В качестве
координаты, задающей положение маятника, выберем
угол q, образованный стержнем с вертикалью,
отсчитываемый против часовой стрелки. Уравнение
движения маятника в полярных координатах можно
записать в виде:
 (9.1)
(9.1)
где 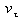 –
касательная компонента скорости грузика
маятника. –
касательная компонента скорости грузика
маятника.
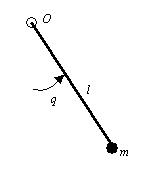
Рис. 9.1. Математический маятник
Для исследования всех возможных
движений маятника (колебательных и вращательных)
начальные условия к системе (9.1) удобно записать в
следующем виде:
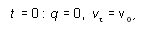 (9.2)
(9.2)
т.е. будем считать, что в начальный
момент маятник находился в положении равновесия,
но ему сообщили некоторый импульс (стукнули по
грузику в горизонтальном направлении).
Задача (9.1)–(9.2) полностью определяет
движение маятника. Для численного решения этой
задачи необходимо, однако, перейти к
безразмерным переменным. В качестве единицы
длины удобно взять длину стержня l, единицу
времени сформировать с помощью ускорения
свободного падения следующим образом: 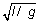 , а единицу скорости
определить как , а единицу скорости
определить как 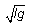 . В
безразмерных переменных задача (9.1)–(9.2)
принимает вид (здесь и далее для обозначения
безразмерных величин использованы те же буквы,
что и для размерных) . В
безразмерных переменных задача (9.1)–(9.2)
принимает вид (здесь и далее для обозначения
безразмерных величин использованы те же буквы,
что и для размерных)
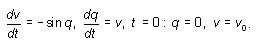 (9.3)
(9.3)
Задача (9.3) содержит один безразмерный
параметр v0 — начальную скорость
грузика, измеренную в единицах 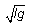 . .
Численная модель
Как и ранее, введем в рассмотрение
дискретные моменты времени tn, в которые
будем находить угол отклонения маятника q(n)
и скорость v(n). Для достаточно малых
интервалов времени dt = tn+1 - tn
отклонения маятника и его скорости в соседние
моменты времени будут связаны алгебраическими
уравнениями:
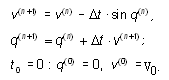 (9.4) (9.4)
Система (9.4) позволяет шаг за шагом, при
малом 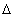 t,
достаточно точно вычислить последовательные
положения маятника, определить период колебаний,
наибольшее отклонение и другие характеристики
колебательного процесса. Угол отклонения
маятника от вертикали примет наибольшее
значение qmax в момент времени, когда
скорость маятника равна нулю. В силу принятых
начальных условий это произойдет через четверть
периода колебаний маятника. Таким образом
устанавливается связь между периодом колебаний
маятника и амплитудой колебаний. Напомним, что
при малых колебаниях период не зависит от
амплитуды и в принятых единицах измерения
времени ( t,
достаточно точно вычислить последовательные
положения маятника, определить период колебаний,
наибольшее отклонение и другие характеристики
колебательного процесса. Угол отклонения
маятника от вертикали примет наибольшее
значение qmax в момент времени, когда
скорость маятника равна нулю. В силу принятых
начальных условий это произойдет через четверть
периода колебаний маятника. Таким образом
устанавливается связь между периодом колебаний
маятника и амплитудой колебаний. Напомним, что
при малых колебаниях период не зависит от
амплитуды и в принятых единицах измерения
времени (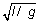 ) равен ) равен 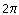 . .
В численном эксперименте интересно определить
величину начальной скорости, при которой маятник
из колебательного режима движения переходит к
вращению. Вращательное движение характеризуется
тем, что угол отклонения, который отсчитывается
против часовой стрелки от нижнего вертикального
положения маятника, не убывает по величине. При
вращательном режиме временной характеристикой
движения является период обращения.
Эксперимент на модели в среде Delphi
Экспериментальная среда для
исследования колебательных систем аналогична
той, какая была в задаче о движении спутника. Для
начала эксперимента необходимо определить шаг
по времени dt и начальную скорость маятника.
Поскольку расчет ведется в безразмерных
единицах, сделать это легко. Выберем такие
значения этих параметров: dt = 0,01, V0 = 0,5.
Построим один график. В окне графиков
нарисовалось три кривых: зависимость угла
отклонения от времени — кривая, близкая к
синусоиде, зависимость угловой скорости от
времени — кривая, близкая к косинусоиде, и
фазовая траектория — кривая, близкая к
окружности, дающая связь между координатой
(углом отклонения) и угловой скоростью.
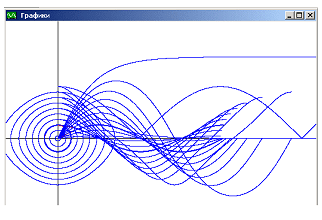
Рис. 9.2. Фазовые кривые и кривые q(t)
и v(t) для конечных колебаний
математического маятника
Для выбора оптимального шага по
времени повторим расчет с dt = 0,001.
Графики функций практически не изменились. В
табл. 1 заметно поправился только период
колебаний. Время счета заметно возросло, поэтому
будем считать этот шаг уже хорошим. Теперь
проведем серию экспериментов с целью
определения зависимости периода колебаний от
амплитуды. Напомним, что при малых амплитудах
этой зависимости нет и период колебаний в
выбранных единицах равен 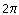 . На рис. 9.2 представлены кривые для
начальных скоростей от 0,1 до 2. Последняя кривая
соответствует вращательному движению маятника.
Значения в табл. 2 позволяют построить
результирующий график зависимости T(A)
нажатием кнопки “Построить” в окне “Итоговый
график”. Чтобы получить детальную картину
искомой зависимости, необходимо провести расчет
колебаний с начальной скоростью, близкой к 2. На рис.
9.3 представлены результаты построения итогового
графика. Правая верхняя точка графика
соответствует вращению, ей приписана амплитуда в
360°, поэтому она выпадает из полученной для
других амплитуд кривой. . На рис. 9.2 представлены кривые для
начальных скоростей от 0,1 до 2. Последняя кривая
соответствует вращательному движению маятника.
Значения в табл. 2 позволяют построить
результирующий график зависимости T(A)
нажатием кнопки “Построить” в окне “Итоговый
график”. Чтобы получить детальную картину
искомой зависимости, необходимо провести расчет
колебаний с начальной скоростью, близкой к 2. На рис.
9.3 представлены результаты построения итогового
графика. Правая верхняя точка графика
соответствует вращению, ей приписана амплитуда в
360°, поэтому она выпадает из полученной для
других амплитуд кривой.
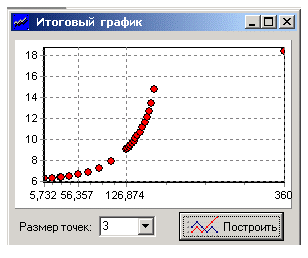
Рис. 9.3. Зависимость периода
колебаний от амплитуды
Пример задания для самостоятельного
исследования
Подробно исследовать вид фазовых
траекторий и функций q(t) и v(t) для
начальных скоростей, близких к 2.
Эксперимент на модели в среде MS Excel
Структура проекта соответствует той,
что описана во введении. На диаграммах
представлены два возможных типа движения
маятника в зависимости от начальных условий:
колебания (первая и вторая диаграммы) и вращение
вокруг точки подвеса.
В качестве самостоятельного задания
можно предложить для этих режимов построить
диаграммы фазовых траекторий.
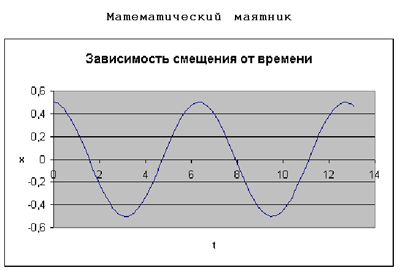
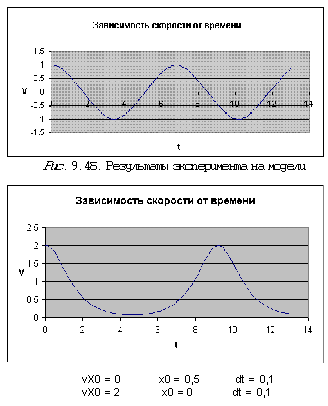
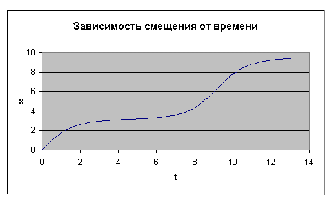
Рис. 9.5. Результаты эксперимента на
модели
Колебательный контур. Резонанс
Постановка задачи
Для исследования вынужденных
колебаний и явления резонанса в учебных целях
удобно взять электрический колебательный
контур, в котором эти явления легко наблюдаются в
натурном эксперименте. Электрический контур,
подлежащий исследованию, показан на рис. 9.6.
Закон Ома для этой замкнутой цепи приводит к
уравнению 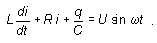 . (9.5) . (9.5)
Заряд на конденсаторе q связан с
силой тока в цепи i уравнением
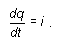 (9.6)
(9.6)
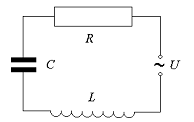
Рис.9.6. Колебательный контур с
периодической внешней эдс
Уравнения (9.5)–(9.6) описывают колебания
заряда и тока в цепи. Для анализа этих колебаний
перейдем к безразмерным переменным. Единицы
измерения заряда Q и времени Т выберем
так, чтобы максимально упростить уравнения
(9.5)–(9.6).
Примем такие представления: 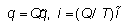 . Уравнения колебаний в
безразмерных переменных (они отмечены знаком
тильда “~”) будут иметь вид . Уравнения колебаний в
безразмерных переменных (они отмечены знаком
тильда “~”) будут иметь вид
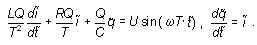
Если в качестве единицы времени взять 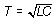 , единицы заряда Q =
CU, то уравнения колебаний принимают вид (знак
“~” опущен, и для единства описания
колебательных процессов сила тока обозначена
буквой v) , единицы заряда Q =
CU, то уравнения колебаний принимают вид (знак
“~” опущен, и для единства описания
колебательных процессов сила тока обозначена
буквой v)
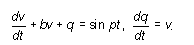 (9.7)
(9.7)
Здесь введены безразмерные
характеристики колебательной системы —
сопротивление 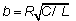 и
безразмерная частота вынуждающей силы и
безразмерная частота вынуждающей силы 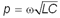 , в которой в
качестве масштаба взята частота собственных
колебаний колебательного контура. Система
уравнений (9.7) описывает вынужденные колебания в
любой линейной колебательной системе с одной
степенью свободы с трением. Для выделения
конкретных колебаний в системе к уравнениям (9.7)
нужно добавить начальные условия. Они задают
свободные колебания, которые в начальный период
складываются с вынужденными колебаниями, но
из-за наличия трения постепенно затухают. Через
достаточно большой промежуток времени остаются
вынужденные колебания, которые не зависят от
начальных условий. Эти предельные колебания и
будут нас интересовать. , в которой в
качестве масштаба взята частота собственных
колебаний колебательного контура. Система
уравнений (9.7) описывает вынужденные колебания в
любой линейной колебательной системе с одной
степенью свободы с трением. Для выделения
конкретных колебаний в системе к уравнениям (9.7)
нужно добавить начальные условия. Они задают
свободные колебания, которые в начальный период
складываются с вынужденными колебаниями, но
из-за наличия трения постепенно затухают. Через
достаточно большой промежуток времени остаются
вынужденные колебания, которые не зависят от
начальных условий. Эти предельные колебания и
будут нас интересовать.
Численная модель
Введем дискретные моменты времени tn,
в которые будем находить величину заряда q(n)
и силу тока v(n). Для достаточно малых
интервалов времени dt = tn+1 - tn
заряд и ток в соседние моменты времени будут
связаны алгебраическими уравнениями:
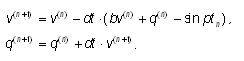 , ,
В начальный момент времени пусть на
конденсаторе отсутствует заряд и ток в цепи
равен нулю:
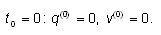
С течением времени будем следить за
тем, как меняется величина тока и величина
заряда. Поскольку предельный режим колебаний при
небольшом сопротивлении наступает через
достаточно длительный переходный режим, за
последовательностью состояний системы удобно
следить на фазовой плоскости (q,v).
Интенсивность установившихся колебаний можно
характеризовать наибольшим значением заряда на
конденсаторе qmax (его квадрат дает
величину “потенциальной” энергии) или
наибольшей величиной силы тока vmax (ее
квадрат дает величину “кинетической” энергии).
Эксперимент на модели в среде Delphi
Рассмотрим, как происходят колебания
заряда и тока в колебательном контуре под
влиянием периодической эдс. Для первого
эксперимента возьмем частоту вынуждающей силы
равной 1, а коэффициент сопротивления 0,5. Шаг по
времени в расчетах должен быть много меньше
единицы, и опыт расчета колебаний маятника
подсказывает, что значение dt = 0,01
является удовлетворительным. Кнопкой “Счет-1”
запускаем эксперимент. В графическом окне
рисуется три кривых (рис. 9.7). Одна кривая в
виде синусоиды описывает изменение со временем
периодической эдс. Амплитуда этой синусоиды в
наших экспериментах будет постоянной. Вторая
кривая, которая после переходного режима
превращается в синусоиду, описывает изменение со
временем силы тока в цепи. Амплитуда этой кривой
зависит от частоты вынуждающей “силы” и в
разных экспериментах может быть разной. Обращаем
внимание на то, что на начальном участке эта
кривая отличается от синусоиды. Третья кривая
изображает фазовую траекторию колебаний — связь
между зарядом и током в процессе колебаний. После
нескольких оборотов вокруг начала координат эта
кривая выходит на предельную кривую —
предельный цикл, которая описывает
установившиеся вынужденные колебания.
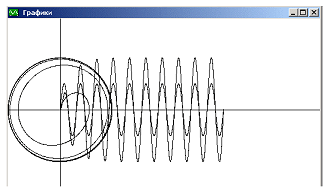
Рис. 9.7. Графики вынужденных колебаний
Амплитуда установившихся колебаний
заряда и тока показана во второй и третьей
колонках табл. 1 компьютерной модели, которую
можно загрузить с сайта “Информатики” (https://inf.1sept.ru,
раздел “Download”). В четвертой и пятой колонках
таблицы показаны сдвиги фазы между заряд — эдс и
сила тока — эдс. Для случая р = 1 сдвиг
фазы между током в цепи и эдс практически
отсутствует. Следует отметить, что сдвиг фазы
вычисляется после совершения большого числа
полных колебаний (в приведенном численном
эксперименте это 10 периодов). За это время из-за
погрешности метода успевает накопиться
дополнительный сдвиг фазы. Чтобы убедиться в
этом, повторим расчет с шагом по времени dt =
0,001 (полезно сменить цвет кривых). Расчет занял
заметно большее время, но сдвиг фазы оказался
меньше. В табл. 2 компьютерной модели показано
изменение заряда на конденсаторе через равные
промежутки времени. В этой таблице, сравнивая
значения заряда в соседних строках, мы также
замечаем накопление ошибки в значении заряда.
Для исследования зависимости
амплитуды силы тока от частоты приложенной к
контуру эдс вернемся к более грубому счету с dt = 0,01
и проведем серию расчетов (11) с р от 0,2 до 2.
Построим итоговый график (кнопка “Построить”).
Максимальное значение амплитуды тока
достигается при частоте р, близкой к единице
(напомним, что за единицу измерения частоты взята
частота свободных колебаний LC-контура). Из
последней колонки табл. 1 видно, что при низких
частотах (p < 1) сила тока опережает эдс,
при резонансе сдвиг фаз отсутствует, а при
высоких частотах (p > 1) сила тока
отстает по фазе от эдс.
Посмотрим теперь, как меняется
резонансная кривая с изменением сопротивления
цепи. Для этого проведем аналогичные расчеты для b
= 0,3 и b = 0,8 (изменим цвет кривых, но
таблицы не чистим!). На итоговом графике
получаются две новые кривые. Для получения более
детальной структуры кривых необходимо в области
максимумов провести дополнительные расчеты.
Зададим интервал частот 0,74–1,28 и для всех
сопротивлений проведем серии по 11 расчетов.
Итоговые резонансные кривые показаны на рис.
9.8.
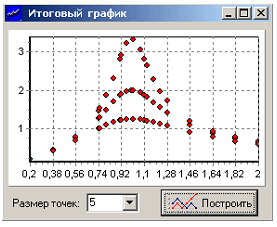
Рис. .9.8. Резонансные кривые
Примеры вопросов для самостоятельного
решения
1. Для b = 0,5 в резонансе
амплитуда силы тока в безразмерных единицах
равна 2. Как найти амплитуду силы тока в размерных
единицах?
Ожидаемый ответ. Для получения
значения силы тока в размерных единицах нужно
безразмерную силу тока умножить на единицу
измерения силы тока: 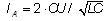 . .
2. Для малого сопротивления резонанс
наступает при безразмерной частоте, близкой к 1.
Как найти эту частоту в Гц?
Ожидаемый ответ. Значение размерной
резонансной частоты можно сосчитать по формуле 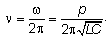
Примеры заданий для самостоятельного
исследования
1. Для различных сопротивлений найти
более точно резонансную частоту и определить, в
какую сторону она смещается с ростом
сопротивления.
2. Для сопротивления b = 1
определить зависимость сдвига фаз между током и
эдс в резонансе от шага по времени.
Эксперимент на модели в среде MS Excel
Результаты моделирования
представлены на рис. 9.9. Параметры каждого
варианта указаны перед диаграммами. На первом
рисунке изображен процесс установления
вынужденных колебаний при частоте вынуждающей
силы, совпадающей с частотой собственных
колебаний контура (черная линия — электрический
заряд на обкладках конденсатора, красная — сила
тока в контуре). На второй диаграмме представлен
процесс установления для случая, когда частота
вынуждающей силы больше частоты собственных
колебаний. Сравнение показывает, что при
несовпадении частот амплитуда установившихся
колебаний уменьшается, что соответствует
результатам моделирования в среде DELPHI.
В качестве самостоятельного
исследовательского задания можно предложить
построить кривую зависимости амплитуды
установившихся колебаний от частоты для разных
коэффициентов затухания.
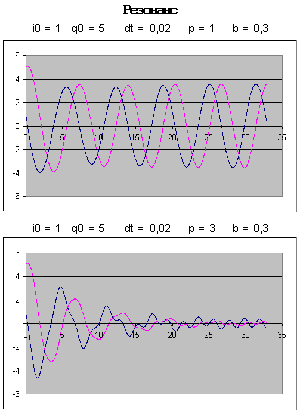
Рис. 9.9. Результаты эксперимента
на модели
Литература
1. Ашихмин В.Н., Гитман М.Б., Келлер И.Э.,
Наймарк О.Б. и др. Введение в математическое
моделирование: Учебное пособие / Под ред. П.В.
Трусова. М.: Логос, 2004, 440 с.
2. Могилев А.В., Пак Н.И., Хеннер Е.К.
Информатика: Учебное пособие для студентов
педагогических вузов / Под ред. Е.К. Хеннера. М.:
Академиа, 1999, 816 с.
3. Корн Г., Корн Т. Справочник по
математике для научных работников и инженеров.
М.: Наука, 1974, 832 с.
4. Макарова Н.В., Титова Ю.Ф. О
подходах к определению базовых понятий раздела
“Моделирование” в школьном курсе информатики //
Информатика и образование, 2004, № 9, с. 2–10.
5. Гейн А.Г. Четыре года спустя, или
Стандарт по информатике: и в нем нам хочется
дойти до самой сути / Информатика, 2005, № 2, с. 3–13.
6. Физический энциклопедический
словарь: т. 3. М.: Советская энциклопедия, 1963.
7. Еремин Е.А. Популярные лекции об
устройстве компьютера. СПб.: BHV-Петербург, 2003, 272 с.
8. Демидович Б.П., Марон И.А. Основы
вычислительной математики. М.: Государственное
издательство физико-математической литературы,
1963, 659 с.
9. Лишнер Р. Секреты Delphi 2. Киев: НИПФ
ДиаСофт Лтд., 1996, 800 с.
10. Петцольд Ч. Программирование для
Windows 95. Т. 1. СПб.: BHV-Петербург, 1997, 752 с.
11. Федоров А., Рогаткин Д. Borland Pascal в
среде Windows. Киев: Диалектика, 1993, 656 с.
12. Еремин Е.А. От нажатия клавиши до
сохранения данных в ОЗУ / Информатика № 20, с. 19–22;
№ 21, с. 26–36; № 22, с. 24–29/2005.
13. Конопка Р. Создание оригинальных
компонент в среде Delphi. Киев: НИПФ ДиаСофт Лтд., 1996,
512 с. |


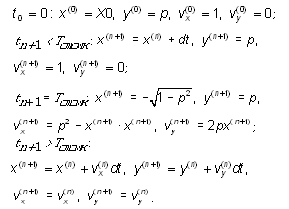 ;
;


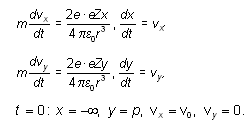
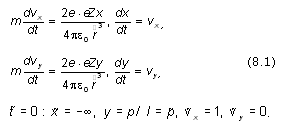
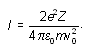 . (8.2)
. (8.2)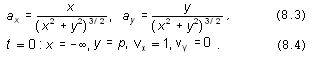
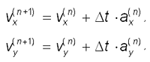 (8.5), (8.6)
(8.5), (8.6)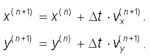 (8.7), (8.8)
(8.7), (8.8)

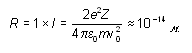


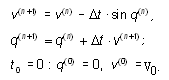 (9.4)
(9.4)




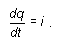 (9.6)
(9.6)
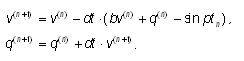 ,
, 

